21.5 マクニマーの検定

マクニマーの検定 (McNemar’s Test) を使うのは：

• 観測を同一個体について行うとき。
• 異なる２つの処理を行ったり、条件を変化させた後の同一カテゴリそれぞれの分布をカウントするとき。

1. マクニマーの検定について
2. マクニマーの検定を実行する
3. マクニマー検定のデータを配置する
4. マクニマーのオプションを設定する
   1. Options for McNemar’s
5. マクニマーの検定を実行する
6. マクニマーの検定の結果を解釈する
   1. カイ二乗
   2. 分割表のサマリー

 

1. マクニマーの検定について

マクニマーの検定 (McNemar’s Test) は、同一個体の測定を繰り返した分割表の分析です。このような表設計を使用するのは：

• 処理の事前と事後の観測データを使用して、ある個体が処理や条件の変化によって影響を受けるか否かを判断するとき。
• 異なる２つの処理や条件によって同一タイプの応答になる結果を比較するとき。例えば、報告の事前と事後における同じ人々の意見 (賛成、反対、分からない) の調査。

マクニマーの検定は、通常の分割表の分析と良く似ています。ただし、同じ処理によって同じ影響を受ける個体については考慮せず、残りのセルの処理によって影響が異なる個体の平均値を使って期待度数を算出します。

 

2. マクニマーの検定を実行する

マクニマーの検定 (McNemar’s Test) を実行するには：

1. ワークシートに適切なデータを入力または配置します。詳しくは、マクニマーの検定のデータを配置するをご覧ください。
   
   
2. McNemar Test レポートを表示して解釈します。詳しくは、マクニマーの検定の結果を解釈するをご覧ください。

 

3. マクニマー検定のデータを配置する

いずれの処理もカテゴリ数が必ず同一になるため、データは行と列が同じ数の表形式である必要があります。

• Tabulated Data：表形式のデータは、観測数を分割表の各セルに配置してあらわしたものです。ワークシートの行と列は、2群のカテゴリに対応します。各群のカテゴリのタイプは、分割表が正方形となるよう必ず同じ数になります。観測数は常に整数となります。

調査した人々の意見に対する報告の効果をあらわす 3 x 3 分割表

Before Report	After Report
	Approve	Disapprove	Don’t Know
Approve	12	24	6
Disapprove	5	32	3
Don’t Know	4	6	4

 

• Raw Data：ワークシートの１つの列にカテゴリを識別する変数を、もう一つの列に対応するカテゴリを配置します。各カテゴリのタイプは同数になります。それぞれの行は１つの観測データに対応するので、データの行数は観測データの総数と同じだけあることになります。
  
  SigmaPlot はこれらのデータから自動的にクロス表を作成し、できあがった分割表に対してマクニマーの検定を実行します。

マクニマーの検定のデータフォーマットの例

 

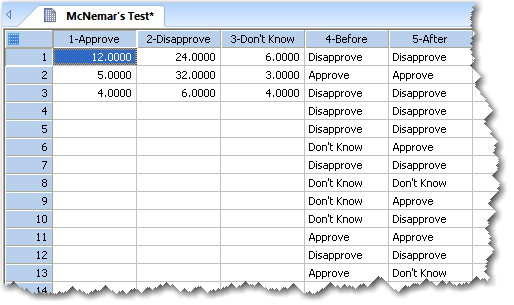上記ワークシートの列１から３までが表形式、列４から５までが観測した生データになります。マクニマーの検定では、列と行が同じ数の表となるデータが必要です。この場合は、 3 x 3 表となります。

 

4. マクニマーのオプションを設定する

イェーツの補正因子 (Yates Correction Factor) を有効にするには、マクニマーの検定オプションを使います。

マクニマーの検定オプションを変更するには：

1. 検定オプションの変更後に検定を実行するに際して、検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
   
   
2. Analysis タブの SigmaStat グループにある Select Test ドロップダウンリストから Chi-square を選択します。
   
   
3. Options をクリックします。
   
   Options for McNemar’s ダイアログボックスが表示されます。
   
   
   
4. Yates Correction Factor を選択すると、この検定レポートにイェーツの補正因子 (Yates Correction Factor) が含まれます。
   
   
5. 検定を続行するには、Run Test をクリックします。
   
   
6. 現在の設定内容を適用して、オプションダイアログを閉じるには、OK をクリックします。

 

4.1 Options for McNemar’s

• Yates Correction Factor：統計的検定に2 x 2 分割表の分析や、マクニマーの検定 (McNemar’s test) など自由度１の χ² 分布を使用する場合、算出される χ² は、χ² 検定統計量の実際の分布と比較すると P 値が非常に小さくなる傾向があります。理論上の χ² 分布は連続的ですが、この χ² 検定統計量の分布は離散的であるからです。
  
  計算される χ² の値を下げてこの食い違いを補うように調整するには、イェーツの連続補正 (Yates Continuity Correction) を使います。イェーツの補正を使うことで、検定を保守的なもの、例えば、P 値が大きくすることで誤判定の結論を下す可能性を低く抑えることができます。イェーツの補正は、2 x 2 分割表や自由度１の χ² 分布を元に P 値を算出するその他の統計で適用します。

 

5. マクニマーの検定を実行する

マクニマーの検定を実行するには、検定するデータを選択する必要があります。検定ウィザードの Select Data パネルを使用して、検定したいデータを含むワークシートの列を選択したり、お持ちのデータがどのような状態でワークシートに配置されているかを指定します。

マクニマーの検定を実行するには：

1. 検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
   
   
2. Analysis タブをクリックします。
   
   
3. SigmaStat グループにある Tests ドロップダウンリストから次を選択します：
   
   Rates and Proportions → McNemar’s Test
   
   検定ウィザードの Data Format ダイアログボックスが表示され、データフォーマットを選択するよう指示されます。
   

   データフォーマットの選択を指示する McNemar’s — Data Format ダイアログ

   
   
4. Data Format ドロップダウンリストから適切なデータフォーマットを選択します。分割表のデータを検定する場合は、Tabulated を選択します。お持ちのデータが生データの形式で配置されている場合は Raw を選択します。詳しくは、マクニマー検定のデータを配置するをご覧ください。
   
   
5. Next をクリックして検定に使用するデータ列を選択します。検定を選択する前に列を選択していれば、選択された列が selected columns リストに表示されます。列をまだ選択していない場合は、データを選択するようダイアログボックスで指示されます。
   
   
6. Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Observations または Data for Category ドロップダウンリストからその列を選択します。
   
   最初に選択した列は、Selected Columns リストの Observation または Category 行に割り当てられ、二番目以降の列は それぞれ次の行に割り当てられます。各行には、選択した列のタイトルが表示されます。生データの場合、ワークシートの列を２つ選択するよう指示されます。表形式のデータの場合は、64 列を上限とする列を選択するよう指示されます。
   
   
7. 選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
   

   データ列を選択するよう指示する McNemar’s — Select Data ダイアログボックス

   
   
8. Finish をクリックすると、検定が実行されます。McNemar’s test レポートが表示されます。詳しくは、マクニマーの検定の結果を解釈するをご覧ください。

 

6. マクニマーの検定の結果を解釈する

マクニマーの検定のレポートには、分割表データのサマリー、その分布を元に算出された χ² 統計量、および P 値が一覧で表示されます。

マクニマーの検定の結果のレポート例

 

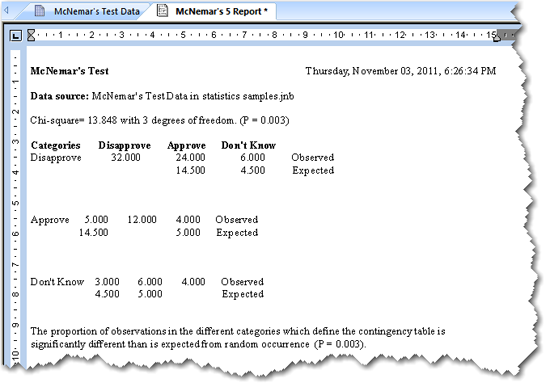結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。また、表示する小数点以下の桁数についても Options ダイアログボックスで設定できます。

 

6.1 カイ二乗

χ² は、テーブルの対角セルにある各個体同じ処理を受ける観測データを無視して、テーブルの各セルの観測度数と期待度数の差の二乗を合計したもので、次式であらわされます：

もし、 χ² の値が大きいものであれば、各個体は処理によって異なる影響を受ける (例えば、期待度数と観測度数の間に差がある) ことを示します。

χ² の値がゼロ付近であれば、分割表のパターンが無作為な度数の分布であるときに期待されるものと差がないことを示します。

• P Value：P 値は、観測数の分布に真の差があると誤って結論付けてしまう確率です (例えば、帰無仮説を誤って棄却する、すなわち第一種の誤り (Type I error) を犯す確率)。 P 値が小さいほど、標本がカテゴリ間に異なる分布をもつ母集団から抽出される確率は高くなります。伝統的には、P < 0.05 であれば、有意差があると結論付けることができます。

 

6.2 分割表のサマリー

テーブルのセル毎に各種統計量があらわされます。

• Observed Counts：分割表のデータを元に得られた１セルあたりの観測数です。
• Expected Frequencies：行と列の百分率を使って予測された分割表の各セルの期待度数です。