例８：重心座標における内接円

サンプルデータ：

• Example8a.gx
• Example8b.gx

a=|BC|, b=|AC|, c=|AB| とし、A, B, C を点 A, B, C の位置ベクトルとするとき、内接円の中心は次式であらわすことができます：

重心座標 (r, s, 1-r-s) を使って点を作成し、その点と三角形の３つの辺で定義される３つの三角形の面積を調べます（パラメータ値 r と s を r+s<1 を満たすように固定して、その点を三角形内部に配置してください）。

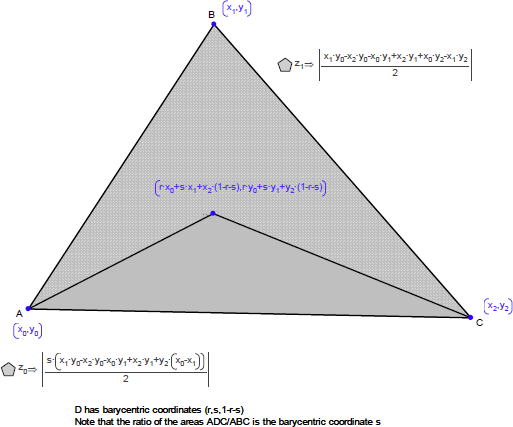
この面積と元の三角形の面積の比はいくつになるでしょうか？

この関係を使用して内心の重心座標の式を証明することができるでしょうか？

この関係を使用して、三角形の辺の長さで外心の重心座標をあらわすことができるでしょうか？