1. Finite Element Methods, PDE Solutions, Applications of FlexPDE, Vol.1, Revision 1
ここでは有限要素法についての精緻な議論を行うわけではありません。FlexPDE の目標の1つは、さまざまな科学、工学分野において、プログラマーや数値解析者にならなくても、有限要素法の恩恵を受けられるようにするということです。有限要素法およびその応用については数百種類の書籍があり、興味のある方には、豊富な材料が提供されています。しかし、FlexPDE で仕事が十分にできれば、これら多量の文献を調べる必要はないでしょう。
とはいえ、FlexPDE の仕組みについて理解したり、ときには何故うまくいかないのかを理解するには、有限要素法の幾つかの考え方を知っておいた方が便利です。これが、本節の目的です。
原理
一般に、偏微分方程式は、エネルギー、運動量、質量などの保存則を数学的に表現するもので、もともと連続量を取り扱います。つまり、微分は、無限小スケールでの差異を観察する有限過程の結果なのです。たとえば、物質内の温度分布は、両端間でなめらかに変化するものと仮定されており、従って、隣接点間での違いを更に詳細に観察することができ、点の間隔がゼロにちかずけば、値は更に接近し、ついには同じになります。
一方、コンピュータは離散数に算術演算を適用します。また、ある時間内に、限定された数しか格納、処理することができません。コンピュータは無限大個の数の処理はできません。それでは、コンピュータを使用して、実際の問題をどのようにして解くのでしょうか?
コンピュータを使って実際のシステムの挙動を近似する多くの方法が行われてきました。有限要素法もその1つで、数十年にわたって成功をおさめてきました。初め、構造力学において、ついで他の分野でも。成功の理由の1つは、全体領域を小部分に分割して積分し、たとえ、微小な誤差があっても総体的な正確さを実現する方法です。物体の形状には殆ど依存せず、従って、実際の複雑な問題に適用できるのです。
全領域上での問題の解にかかわりなく、小部分での解は低次多項式で近似できる、というのが基本的な仮定になっています。これは、よく知られたテーラー展開に密接に関連しています。つまり、テーラー展開では、関数の局所的挙動を数個の多項式の項で表現します。
例えば、2次元の熱伝導問題では領域を多数の三角形に分割すれば、各部分での温度は、例えば、放物面でうまく表現できます。小部分をつなぎ合わせると、解 (微分では多分ないが) の差分的限定連続性の仮定に従うハーレクイン曲面を得ます。三角形によるつぎはぎ細工を計算「メッシュ」といい、頂点あるいは他の点での標本点をメッシュの「ノード」 (節点) といいます。
3次元においても類似の過程をとりますが、この場合には、領域を四面体で分割します。
では、小部分の形状をどのように決めるのでしょうか ?
- 標本値を三角形あるいは四面体の各頂点に割り当てます。これら頂点の値は数個の三角形あるいは四面体が共有します。
- 近似関数を偏微分方程式に代入します。
- その結果に重要度重み付き関数を乗じ、頂点をとりまく三角形上での積分を行います。
- 誤差を最小にするように頂点値を決めます。
この過程は、「重み付き残差法」として、知られ連続の PDE 問題を頂点値を離散最小値問題に変換します。この方法は、PDE を領域の全点に強制的に厳密にあわせるのではなく、三角形分割に関して積分的な意味で正しくするため、「弱形式」と呼ばれています。
標本値の場所と数は、内挿方法によって異なります。FlexPDE では、二次の内挿 (頂点および三角形各辺の中点を使用して) あるいは、三次の内挿 (頂点および各辺に沿った 2点を使用して) を使用しています。これ以外の方法を使用し、異なるタイプの有限要素法を生み出すこともできます。
境界条件
偏微分方程式系の基本要素は、一群の境界条件で、これによってユニークな解が得られます。境界条件は、積分計算で現れる積分定数に類似しています。
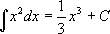
において、C は任意の定数です。
右辺を微分すれば、C の値に無関係にもとの被積分関数が得られます。同様に、
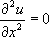
を解くには、2回積分を行う必要があります。1回目の積分で、
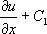
が得られ、2回目で
C1x + C2
となります。これらの積分定数は、問題を解く場合、境界条件として与える必要があります。
これらの例から明らかなように、PDE では微分が入れ子になっているので、多くの積分定数が存在します。一般的には、これら定数は、間隔終端での値、端点での値および微分などとして与えられます。実際に最もよく使用されるのは、領域端点における値あるいは微分条件を指定するものです。2または3次元の場合、全体の曲線あるいは曲面上に適用される値あるいは微分条件は、各積分路端点での条件を与えます。
部分積分および自然境界条件
FlexPDE において、有限要素方程式を扱う場合に適用する基本的な技法は「部分積分」で、これによって、被微分積分関数の次数を落としたり、PDE 系の微分境界条件を直ちに作ることができます。
部分積分は、通常以下のように表現されます。
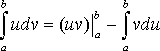
例えば、部分積分を 2あるいは 3次元領域のベクトル・ダイバージェンスに適用すると、ダイバージェンス定理が得られます。2次元で書くと、
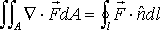
上式は、領域内の積分と外側境界を横切る流束を関係づけます(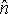 は表面外部の法線単位ベクトル)。 は表面外部の法線単位ベクトル)。
部分積分は、FlexPDE が PDE 系を解釈し、解く場合の方法に広く影響を及ぼしています。
部分積分を重み付き残差法に適用すると、三角形セル間の境界での有限要素近似の流束保存特性を表現することになり、被面積分関数の値を指定することによって、系と外界の干渉の定義方法も提供してくれます。
被面積分関数の値は、PDE 系の「自然」境界条件です。この用語は、変分法でも同様の意味で使われています。
例えば、熱方程式、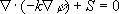 において、部分積分をすると、ダイバージェンス項が得られます。 において、部分積分をすると、ダイバージェンス項が得られます。
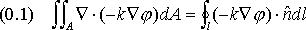
右辺は、外部境界を横切る熱流束で、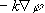 は自然境界条件として、与えなくてはなりません(BC の値を代わりに適用できない場合)。 は自然境界条件として、与えなくてはなりません(BC の値を代わりに適用できない場合)。
2つの材質間で、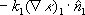 は、材質1から出る熱エネルギーを表します。同様に、 は、材質1から出る熱エネルギーを表します。同様に、
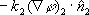 は、同地点において材質2から出る熱エネルギーを表します。材質1からの外向き法線は材質2からの外向き法線の負であるので、境界における流束合計は、 は、同地点において材質2から出る熱エネルギーを表します。材質1からの外向き法線は材質2からの外向き法線の負であるので、境界における流束合計は、
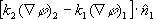 となり、これが、接合部における自然境界条件となります。この場合、2つの流束項の合計をゼロにすべく、エネルギーの保存を図りたいので、内部自然境界条件は接合部でゼロとなります。これが、FlexPDE のデフォルト値になっています。 となり、これが、接合部における自然境界条件となります。この場合、2つの流束項の合計をゼロにすべく、エネルギーの保存を図りたいので、内部自然境界条件は接合部でゼロとなります。これが、FlexPDE のデフォルト値になっています。
便利な積分規則
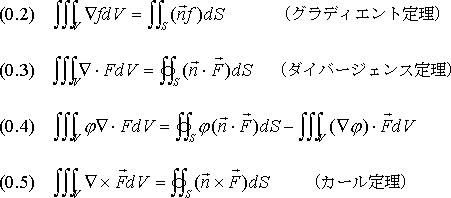
適用メッシュによる細分割
既述しましたように、「あるスケール」においては、低次多項式で、解の近似が十分に行えます。しかし、メッシュがどこで密あるか、疎であるかはいつも明らかなわけではありません。この問題に対処すべく、FlexPDE では「適応メッシュによる細分割」法を採用しています。ユーザが想定する問題領域は、領域サイズおよびユーザの入力制御に従い、三角形メッシュに分割されます。ついで、問題を構築し、解を得ます。この場合に、重み付き残差法によるセル積分をクロスチェックして精度の見積もりを行います。積分の精度に問題がある場所では、三角形を更に分割して新たなメッシュを作り、再計算を行います。この過程は、局所的に近似精度がユーザが指定した閾値を満足するまで繰り返し、行われます。局所的な精度を満足したとしても、必ずしも絶対精度を保証するものではありません。全体の精度は、誤差の累積あるいは相殺状況によって、局所的精度に比べ良くも悪くもなります。
時間積分
上記で説明した有限要素法は、境界値問題を扱うにはいいのですが、初期値問題については、有限要素法でもできますが、他の方法の方がよく使用されています。FlexPDE では、C.W.Gear が導入した可変次数の陰的な後退差分法 (BDM, Backward Difference Method) を用いています。大抵の場合、二次で安定性、平滑度、計算速度の調和を最上にすることができますので、これが FlexPDE のデフォルトとなっています。この方法では、2つの既知の値と1つの未来値 (未知) を用いて、各ノード値に時間順に二次式を当てはめ、次の時間において、ノード値配列について連成問題を解いています。もう 1ステップ後退すると、各ノード値に時間挙動を表す 4点拡張式の3次項の大きさの推定が可能になります。これら 3次項が大きい場合には、時間ステップを短縮し、場合によっては、現ステップの繰り返し計算も行います。
|

