2. 飽和計画の例

ランス・レッグストロングは、早春自転車競技大会に備えて自転車の最終調整を行います。大会が開催されるまでに残された期間は1週間です。彼は4分の１マイルのトラックを 8周だけ走行して、７つの因子を検定することにしました。以下に示すのはランスが作成した計画表で、Design‐Expert のデフォルトの factorial タブに用意された “2‐Level Factorial” 計画ビルダーでセットアップ可能です。この計画は、因子が “saturated”、すなわち、与えられた数の試行に対してこれ以上因子を追加できない状態にあります（この事例の着想は、Statistics for Experimenters, 2nd Edition（Wiley, 2005）by Box, Hunter and Hunter（“BHH”）から来ています。BHH は第6.5章で、取り扱う因子が少ないため結果は以下に示すものとは異なりますが、これと非常に似た研究を報告しています）。

「テレビの調子が悪くてうまく映らない場合、ある場所をキックすれば、少なくとも当分の間は問題が解消することがよくあると思います。しかし、長期的解決策を講じるには、この不具合の起こる真の理由を突き止める必要があります。一般に、問題は一時的に解消されるか、抜本的に解決されるかのいずれかです。解消と解決の両方を仲立ちするのが実験計画法 DOE です。」 ‐‐ Box, Hunter and Hunter.

実験計画と結果

Std	Run	A: Seat	B: Tires psi	C: Handle Bars	D: Helmet Brand	E: Gear	F: Wheel covers	G: Generator	Time 1/4 mile secs
1	2	Up	40	Up	Windy	Low	Off	Off	77
2	1	Down	40	Up	Atlas	High	Off	On	74
3	4	Up	50	Up	Atlas	Low	On	On	82
4	7	Down	50	Up	Windy	High	On	Off	47
5	6	Up	40	Down	Windy	High	On	On	72
6	3	Down	40	Down	Atlas	Low	On	Off	77
7	8	Up	50	Down	Atlas	High	Off	Off	48
8	5	Down	50	Down	Windy	Low	Off	On	83

 

以下の評価結果を見てすぐにお分かりいただけるように、これは主効果のすべてが２因子交互作用と交絡する分解能 III 計画のひとつです（分解能が低い計画であるという注意をユーザーに喚起するため、Design‐Expert の計画ビルダーでこれらは赤のフラグで表示されます）。

Design-Expert の２水準完全実施要因計画ビルダー

 

ランスは分解能 V またはそれ以上の実験を実行したいと考えます。これなら、主効果とその交互作用を明確に評価できるからです。残念なことに、Stat‐Ease 社の統計学者によって考案された “min‐run Res V” 計画（別名 “MR5”）を使えば、試行回数が最低でも30回は必要となります。しかし、大会までに残された期間はわずかしかありません。試行数 30 回は多すぎます。ランスはしばらく考えて、中間の分解能 IV 計画（現在、Design‐ Expert に黄色で警告されている計画）を選択しようとしますが、それでも16回の試行が必要なので、8回の試行だけで実行できる分解能の低い分解能 III を実行することに決めました。

データ入力の時間を節約しましょう。“Help” -> “Tutorial Data” -> “Biker” をクリックして、実験結果を読み込みます。データを一通り眺めたら、左側にある “Evaluation” ノードをクリックして、計画のエイリアス構造を点検してください。試行数の少ないこの計画では、 Design‐Expert は主効果の順序に対する応答しかモデル化できないと判断している点に注意してください。プログラムは 3FI 以上の項は無視する設定がなされているので、２因子交互作用（2FI）までのエイリアス化を表す結果が生成されることになります。

自転車選手の実験の評価

 

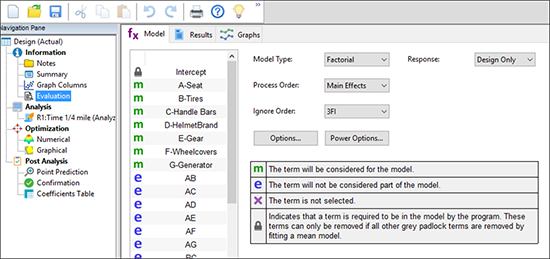それでは、データウィンドウの上部にある “Results” ボタンを押してから、“Aliases”タブを選択して、この事例における分解能 III 計画の試行のみに関する影響が表示されます。

自転車走行タイムトライアルの第一ブロックに関するエイリアス構造

 

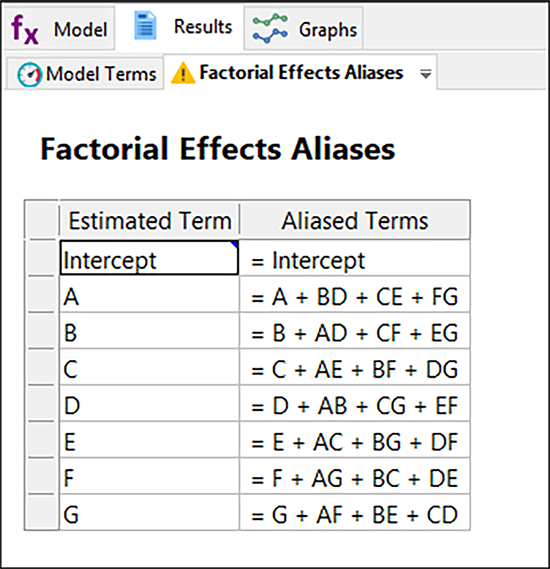表示された計画は全体の 1/16 番目です。従って、以降の効果もそれぞれ他の 15 の効果でエイリアス化されることになりますが、その殆どは画面を不必要に占有してしまうため、デフォルトでは無視するよう設定されています。この出力結果は、いずれの主効果も３つの２因子交互作用と交絡することを表しています。

評価レポートの残りの内容については、ここでは触れません。左側の Analysis ブランチにある “Time 1/4 mile” ノードをクリックして、画面ウィンドウ上部の “Effects” をクリックしてください。最大効果を右から順番に３つクリックしてください（以下の図のようにマウスで範囲を選択しても同じです）。

効果グラフ：３つの最大効果を選択

 

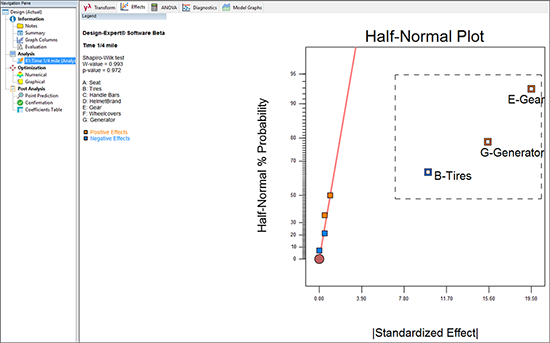次のパレート図において、表示されたチャート上の最大のバー（E）を右クリックすれば、以下のようにそのエイリアスが表示されます。

ラベルEのバーについてエイリアスを表示した効果のPareto Chart

 

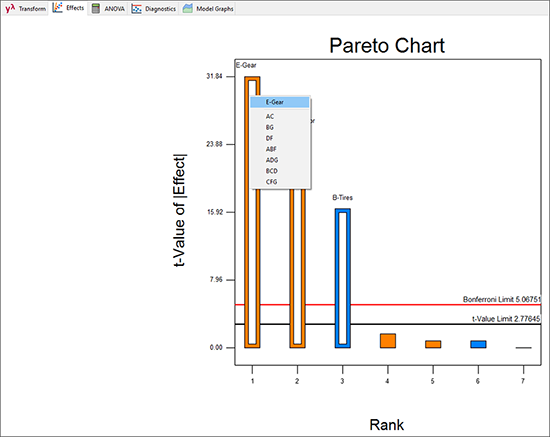因子 B（タイヤ）、E（ギア）、G（発電機）は、明らかに有意です。“ANOVA” をクリックして、これを統計的に検定してみましょう。ANOVA 画面が現れる前に、この計画がエイリアス化されていることを思い起こさせる以下の警告ダイアログが表示されます。

エイリアスの警告ダイアログ

 

この内容は既に計画の評価段階で承知していますので、“No” をクリックして続行してください（オプション：Yes をクリックした場合は、前の画面に戻ってリストが表示されます。内容を確認したら ANOVA ボタンをクリックしてください）。

ANOVA 出力結果

 

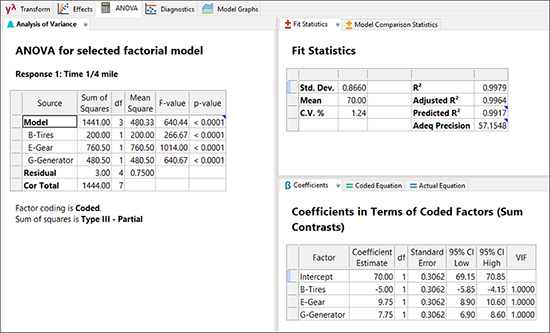ランスは、実験データをうまく当てはめることができました。因子 B の係数が負の値であることから、タイヤの固さが固いほどトラックの走行にかかる時間は落ちるようです。また他方で、因子 E と G の係数が正の値を示していることから、ギアを高くし、発電機をオフにしておいた方が、速度が出ることがわかります。一見したところ、このアプローチは全体として非常に科学的で決定的であるかのように見えます。実際、ランスはこの実験結果に基づいて自転車を最終調整した結果、レースに出場して優勝したのですから！

しかし、ランスの友人（であり個人的なコーチでもある）シェリル・ソングバードは、この結論が誤りであることに気が付きます。彼女が指摘するのは、この計画の主効果はいずれも２因子交互作用と交絡している点です。真に有意な要因は、交絡する交互作用のどれか一つである可能性もあるわけです。「この件をクリアするまでは、少なくとも、もう１回実験する必要があるね」とシェリルは言います。ランスは「それはいい考えだ」とうんざりしながら答えました。自転車の理想的なセッティングに関する疑念が残ったままであることが分かり、これでおちおち休むことはできないと気付いたからです。