9.4 Dynamic Models (動態モデル)

このフォルダーには、Analytica の Dynamic() 関数を利用して動態シミュレーション (周期的に変化するモデリング) を実行するモデルが含まれています。

• Disease establishment (病気の発生)
  このモデルは、 魚の個体数と接触感染によるウイルス性疾患の発生を時系列で予測します。
  
  
• Leveling (平坦化)
  この例は、期間中の仕事量と空き時間を計算し、利用可能なスタッフ数に基づいてスタッフの活動を時系列で平坦化するものです。
  
  
• Markov Chain (マルコフ連鎖)
  このモデルは、動的時間を使用してマルコフ過程をシミュレーションする方法を紹介します。事例では、マルコフ過程としてモデル化された時間とともに推移する入院患者数を推定します。
  
  
• Mass-Spring-Damper (質量-ばね-ダンパー系)
  このモデルは、 典型的な質量-ばね-減衰の自由系 (free mass-spring-damper system) をシミュレーションするものです。"free system" とは、質量に作用する時間依存の駆動力や変異がないことを意味します。このような系の解は、通常、適切な初期条件を与えた均一な２次微分方程式のセットから決定されます。このモデルでは、運動学的変数 (変位、速度、加速度) が典型的な運動学的方程式と結び付けられ、動的変数 (ばね力と減衰力) がニュートンの第２法則によって加速度と系の質量に結び付けられます。インプットとして与えるのは各種初期条件 (ばね定数、減衰定数、質量、初期変位、初期速度) とモデルの実行時間です。この動態モデルによって生成されるグラフによる解は、微分方程式によって求める解と同じになります。
  
  
• Optimal Path Dynamic Programming (動的最適経路プログラミング)
  このモデルでは、逐次決定問題の 単純な動的プログラミングによる解法を紹介します。タイムステップの最後に既知の報酬を支払い、移動のたびに既知のコストがかかる決定論的環境を考慮に入れた有限タイムステップの最適経路を計算します。
  
  
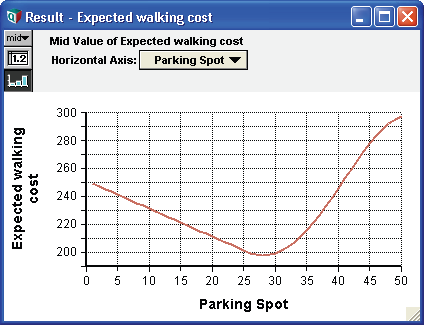
• Parking Space Selection (駐車場の選択)
  不確実性を伴う逐次的決定問題を説明した単純な動態シミュレーションの事例です。レストランに行くまでにかかる時間を最小化する最適な駐車場を見つけることになります。この事例では、 Dynamic() 関数を Time 以外のインデックスに対して使用する方法と、動的な再帰が将来の値 (過去の値ではなく) に基づく逆再帰 (reverse-recurrence) の使用を紹介します。
  
  
  
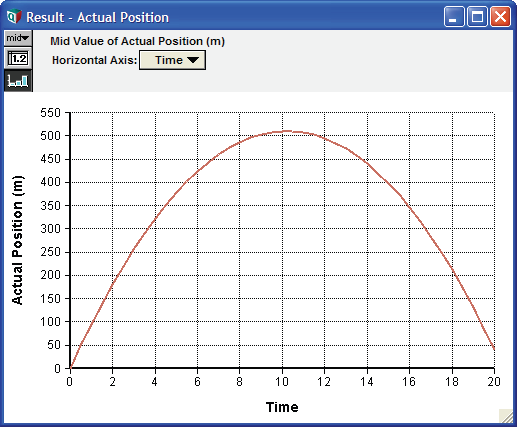
• Projectile Motion (放物運動)
  システム変数 Time と Dynamic() 関数を使用して時間とともに変化する動作をモデル化する方法を紹介します。この例では、放物運動をモデル化します。
  
  
  
• Tunnel through earth (地球を貫くトンネル)
  地球の中心をまっすぐに貫くトンネルを想像してみてください。 ここに足を踏み入れると、地球の反対側に出るまでにどれほどかかるでしょうか？地球の中心を通るとどれだけ早く移動できるでしょうか？この単純な旅の動態シミュレーションを使って調べてください。
  
  
• Unequal time steps (不等間隔のタイムステップ)
  このモデルは、不等間隔のタイムステップで Time を定義した時間を使って成長を計算する動態変数の事例を紹介します。これは、指数または線形の増加または減少、すなわち、ある時点の値が直前の時点の値に対して指数または線形的に依存する動態変数の事例です。