9.3 Decision Analysis (決定分析)
このフォルダには、決定分析 (decision analysis) の実例を紹介するモデルが含まれています。
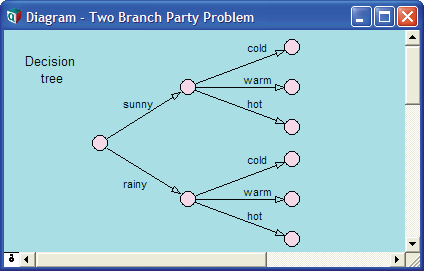
- Two Branch Party Tree (パーティ決定の2段階分岐ツリー)
このモデルの作者は、パーティを開催したいと思っていますが、どこで開いたら良いか決めかねています。このモデルは、Analytica で2段階の決定木をモデル化する方法を紹介します。
- Beta Updating (ベータ更新)
このモデルは、ベータ分布を使用してコインの表が出ると思う主観的確率 (beliefs) のベイズ更新 (Bayesian update) を実行します。
- Biotech R&D Portfolio (バイオテクノロジー研究開発のポートフォリオ)
この複数プロジェクトの研究開発 (R&D) 評価は、バイオ関連企業が直面する研究開発の典型的な決定問題をモデル化したものです。
- Diversification Illustration (多角化の図解)
このモデルは、一連の投資の高まりをふまえて多角化することの効果を表示するひとつの手法
Blitzogram™ の事例です。このモデルの事例は、Sam Savage 氏による Informs Transactions on Education, Vol. 1., No. 2 (Jan. 2001) の “Blizograms - Interactive Histograms” を利用しています。詳しくは下記をごらんください:
- Expected Value of Sampling Information (EVSI):サンプリング情報の期待値
EVSI for further treatment trials モデルは、観察資料から得られる価値がどの程度得られるかを決定を行う前に測る尺度 EVSI を計算します。このモデルでは、ある薬品承認機関が特定の新規治療法を承認すべきか否かを決定します。決定を行う前に、追加の臨床試験を要求するオプションがあります。EVSI により、追加の試験から得られる情報の期待値が得られます。
- Gibbs Sampling in Bayesian Network (ベイジアンネットワークにおけるギブスサンプリング)
このモデルは、確率的シミュレーション (Stochastic Simulation) とも呼ばれるギブスサンプリング手法を使用して ベイジアンネットワーク問題を解きます。マルコフ連鎖モンテカルロシミュレーションの事例の1つです。この実装では、複数のシミュレーションが同時に実行されます。モデル内にある任意の変数を観測のサブセットに指定して (プルダウンメニューを使用)、他の変数の事後確率を計算します。この手法の詳細につきましては、S. L. Lauritzen and D. J. Spiegelhalter, “Local Computations with Probabilities on Graphical Structures and Their Application to Expert Systems,” Journal Royal Statistical Society Series B50:2, 1984, p. 157-224 をご覧ください。
- LEV R&D Strategy (低排出自動車の研究開発戦略)
これは低排出自動車 (LEV) の動力に関する幾つかの選択肢のうち、研究開発の決定分析を投資戦略的にモデル化した例です。
- Marginal Analysis for Control of SO2 Emissions (SO2 排出規制の限界分析)
このモデルは、経済的にもっとも効果的な浄化水準になるような政策代替案を決定する利益/コストの限界分析を紹介するものです。
- Multi-attribute Utility Analysis (多属性効用分析)
このモデルは、 自動車に関する多属性効用分析の事例です。各種属性にドライバー毎に異なる重要度の重みをつけて各自動車を分析します。
- Newton-Raphson Method (ニュートン=ラフソン法)
このモデルには、 f(x)=0 の根を求めるための最もパワフルで良く知られている数値手法である Newton-Raphson 法 (または、単に Newton 法) が実装されています。
- Nonsymmetric Tree (非対称ツリー)
このモデルは、決定木の用語を使用して非対称の決定木の事例を Analytica に構成します。
- Party With Forecast (パーティと天気予報)
このモデルは、 パーティの主催者が直面する問題を紹介します。不確実な天気に直面して、パーティーを開催するのに最も良い場所はどこでしょうか?主催者がパーティに割り当てる値は、選択する場所と結果としての天気の関数です。
このモデルは、基本パーティモデルを拡張して、不完全情報 (この例では天気予報) の値を表示するためにベイズ更新 (Bayesian updating) を使用しています。
- Plane catching decision with EVIU (EVIU を使った飛行機確保の決定)
不確実性を含む期待値 (EVIU: Expected Value of Including Uncertainty) とは、不確実性を確率分布としてモデル内に含めたときに得られる意思決定を、パラメータに決定論的な見積もりしか使用しなかった場合と比較したときの質的改善をあらわします。
このモデルは、飛行場のフライトに間に合うためには何時までに家を出たらよいかを調べるモデルの使用を通じて、どのように EVIU が算出されるかを紹介します。
- Probability of Gaussian Region (Importance Sampling)
このモデルは、importance sampling (重要度サンプリング) の手法を紹介します。重要度サンプリングとは、モンテカルロサンプリングの一種で、非常に起こりにくい事象のサンプリングに利用することができます。サンプルサイズが限定されたストレートなモンテカルロでは、被覆領域が非常に狭くなり、確率が非常に低くなります。この事例では、 ガウス分布内の非常に狭い領域の確率を実際に見積もります。
- Supply and Demand (供給と需要)
このモデルは、利潤関数が平均需要値の周囲に非対称であるときに利益を最大化するのに必要な供給水準を計算します。
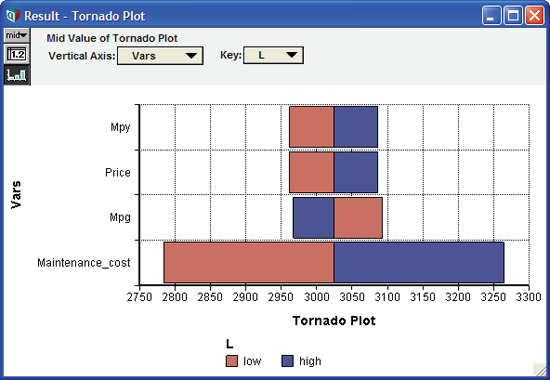
- Tornado Diagrams (トルネードダイアグラム)
トルネードダイアグラムとは、選択する変数の違いに対する結果の感度をあらわすのに使用する一般的なツールです。トルネードダイアグラムの背後にある基本分析では、インプット変数が一度に1つしか考慮されず、その他の変数は、それぞれの名目値 (nominal value) で固定されます。一般に、各インプットの値には low と hight を選択し、一度に1つの変数を変化させてアウトプットの値を計算します。このサンプルモデルでは、high と low の値を選択する2つの手法を紹介します。1つ目は、 low=90% of nominal, high=110% of nominal という具合にすべてのインプットを同一の相対値に変化させるものです。2つ目は、すべてのインプットを与えられた2つのフラクタイル (分位数) 間で変化させるものです。これは、インプットが不確実性変数であるときだけ有効となります。例:low=10% fractile, high=90% fractile, nominal=50% fractile
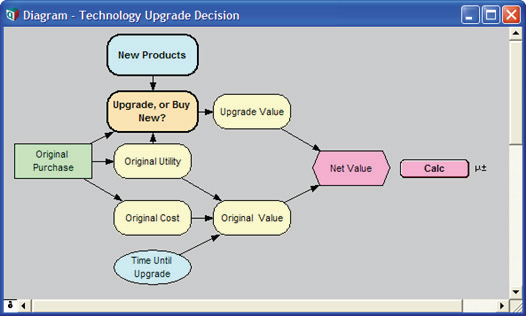
- Upgrade Decision (アップグレードの決定)
このモデルは、今日の世界でしばしば直面する問題、すなわち、不確実な将来の製品と価格を前にしてどのテクノロジーを現在購入するかという決定をあらわします。