更新日： 24/06/13

SigmaPlot 基本操作ガイド - 等分散性の検定

SigmaPlot による等分散性の検定に関する使用例を説明いたします。

等分散性の検定 (Equal Variance Test) とは
例題
操作手順

等分散性の検定 (Equal Variance Test) とは

等分散性の検定

等分散は、2 群以上のデータ分布が等しく分散していることを示します。等分散性が満たされていると、各群のデータの分布が一様であるため、統計的な検定やモデルの推定において正確な結果を得やすくなります。等分散性が満たされていないと、偏りが生じたり、誤った結論に導く可能性が高くなります。

等分散性の検定は、2 群以上のデータについて各々の母集団の分散が等しいかどうかを調べます。等分散性を満たしていることを前提とする代表的な統計手法は、t 検定と ANOVA です。等分散性の検定 (F検定、バートレット検定、ルビーン検定、ブラウン・フォーサイス検定等) によりその仮定を検証します。

ブラウン・フォーサイス (Brown-Forsythe) 検定

SigmaPlot には、ブラウン・フォーサイス検定が用意されています。ブラウン・フォーサイス検定は、2群以上の分散の等質性を検定します。ブラウン・フォーサイス検定は、異なるサンプルサイズや異なる分散を持つグループ間のデータに対しても頑健であり、非正規分布に対しても有効であるため幅広いデータの解析に適しています。

ブラウン・フォーサイス検定のアルゴリズムは次で説明されます。

データセットをグループに分割する。(t 検定または ANOVA のデータ)
各グループについて、グループの各観測値からグループの中央値を減算する。その結果を絶対値にする。
サンプル数が 20 未満のグループの場合、ステップ 2 の結果からすべてのゼロを削除する。
(グループ内の分散のロバストな推定に寄与しない点を削除する補正)
ステップ 3 のデータを使用しグループに対し One Way ANOVA を実行。
F 検定の結果はブラウン・フォーサイス検定の統計量であり、分散分析の結果として得られる P 値は
ブラウンフォーサイス検定の P 値です。

上記手順を行うことで、得られた結果がレポートの Equal Variance Test (Brown-Forsythe) と一致することを確認できます。
ステップ 3 については、他にも文献で提案されるデータ補正の実施方法があります。たとえば、グループごとにゼロを 1 つだけ削除する。ゼロをグループ内で次の最小値に置き換えることを提案する人もいます。

次の例題について、SigmaPlot を使用し等分散性の検定を実施する手順を紹介します。

例題

部品製造機器のリプレイスを検討しています。現在使用している高価な機器 A と候補に挙がった安価な機器 B を比較したいと思います。

機器 A と機器 B で製造した部品を各々 8 つサンプリングし、基準値からの誤差を測定しました。機器 A と機器 B の製造部品の加工精度の違いを推定します。

表1
機器 A	機器 B
0.00130	0.00390
0.00020	0.00175
0.00160	0.00310
0.00140	0.00021
0.00080	0.00055
0.00070	0.00171
0.00050	0.00297
0.00110	0.00670

操作手順

SigmaPlot の Σ メニューをクリックして New → Notebook を実行しワークシート (Data 1) を表示します。

下図のようにワークシートにデータを入力します。

続いて Analysis タブ→ Tests → Compare Two Groups → t-test... を実行します。

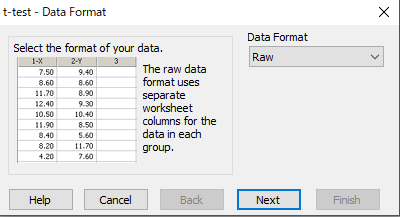
Raw 形式のまま、Next ボタンをクリックします。

ワークシートから変数を選択して (もしくは Data for Data プルダウンメニューから各々の変数を選択して) 変数を割り当てます。

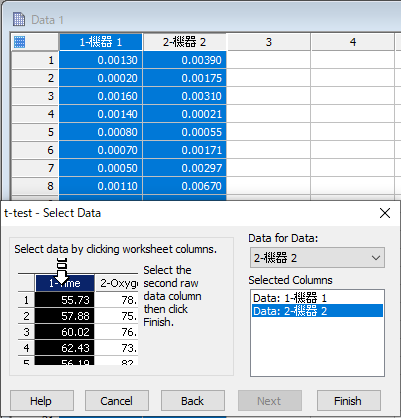
Finish ボタンをクリックします。

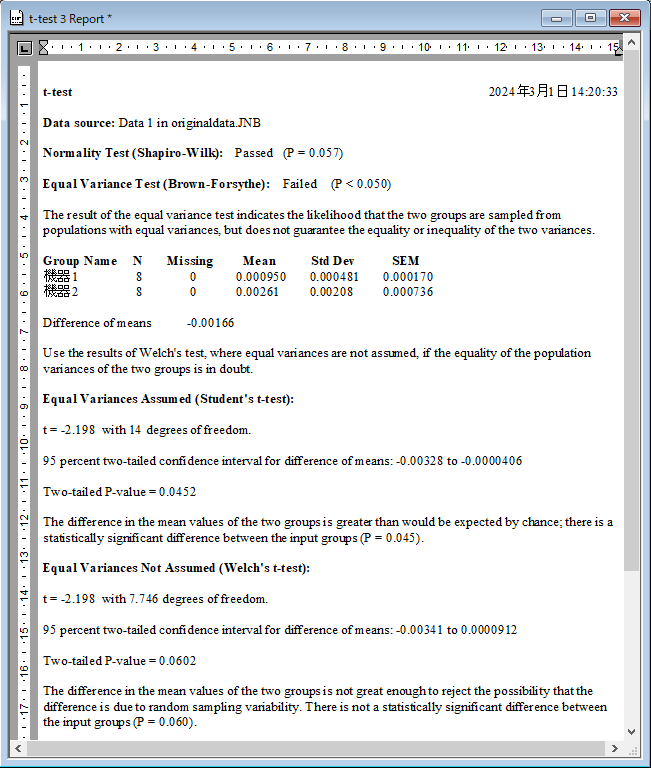
t-test のレポートが出力されます。

帰無仮説 H₀: 各群の分散は等しい
対立仮説 H₁: 各群の分散は等しくない

有意水準 (帰無仮説を棄却するかを判断する基準となる確率) は α=0.05 とします。

p 値が α=0.05 より小さい場合は、帰無仮説 H₀ は棄却され対立仮説 H₁ が採択されます。

等分散性の検定「Equal Variance Test (Brown-Forsythe)」は「Failed」と表示されており、P 値が有意水準 0.05 より小さいことを示しています。帰無仮説は棄却され、対立仮説が採択されます。ふたつの群は等分散ではないと言えます。機器 A と機器 B の製造部品の加工精度 (分散) には違いがありそうです。