|
| サイトマップ | |
|
 |
| サイトマップ | |
|
SigmaPlot による記述統計に関する使用例を説明いたします。
カイ二乗検定 (Chi-square test) は統計的手法のひとつであり、カテゴリや頻度を表すデータを分析し、2つまたはそれ以上のカテゴリ変数間の関連性や独立性を調べるために用いられます。
一般的に利用されるものはピアソンが提唱したピアソンのカイ二乗検定 (Pearson's chi-square test) です。
ここでは、化粧品 A を購入したか、また事前に 化粧品 A の CM を見たかについてのアンケート調査データを利用して、SigmaPlot でのカイ二乗検定を実施する手順を紹介します。
アンケート結果は下の表1のとおりです。
「化粧品 A の購入と CM の視聴」との間に関連性があるか、カイ二乗検定を用いて調べます。
| CM を見た | CM を見ていない | 合計 | |
| 購入した | 33 | 20 | 53 |
| 購入していない | 27 | 40 | 67 |
| 合計 | 60 | 60 | 120 |
帰無仮説及び対立仮説の定義は次のとおりです。
有意水準 (帰無仮説を棄却するかを判断する基準となる確率) は α = 0.05 とします。
α = 0.05 より小さい場合、帰無仮説 H0 は棄却され、独立ではない(関連している)という対立仮説が採択されます。
SigmaPlot の Σ メニューをクリックして New → Worksheet を選択し新規ワークシートを表示します。
下図のようにワークシートにデータを入力します。

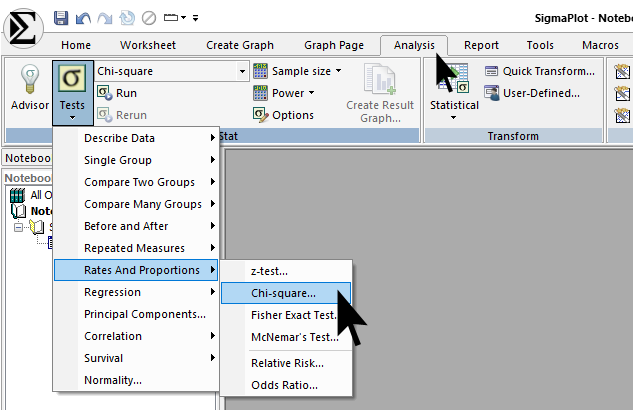
続いて Analysis タブ→ Tests → Rates And Proportions → Chi-square... を選択します。
Data Format に Tabulated Data を選択します。
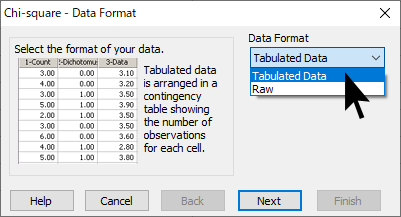
Observations (観測値) が表示されたら入力したデータをドラッグして、Finish ボタンをクリックします。
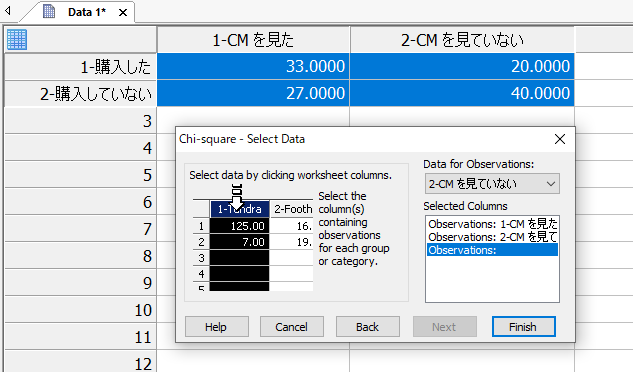
| ※ 分割表の期待値の 20% 以上が 5 未満の場合、カイ二乗検定は不正確になる可能性があります。 次のメッセージが表示され、フィッシャーの正確検定 (Fisher exact test) の実行を促される場合があります。 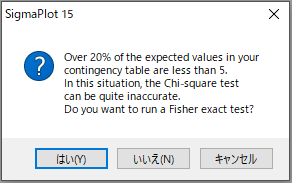 「はい」をクリックした場合は、フィッシャーの正確検定のレポートが出力されます。 |
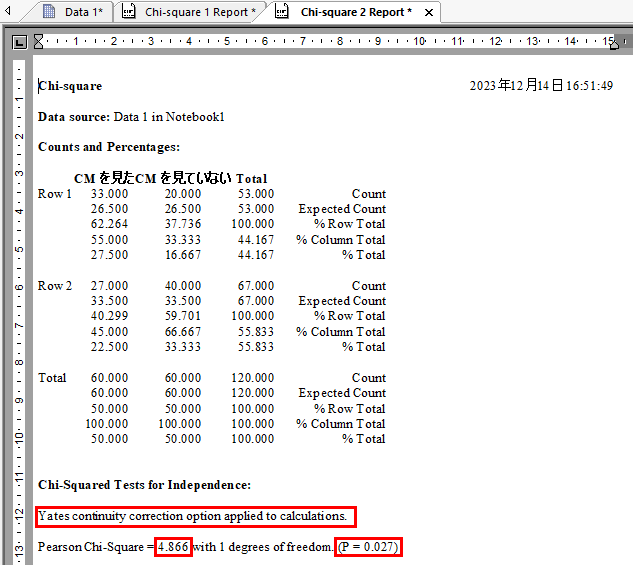
Finish ボタンをクリックすると、カイ二乗検定のレポートが出力されます。
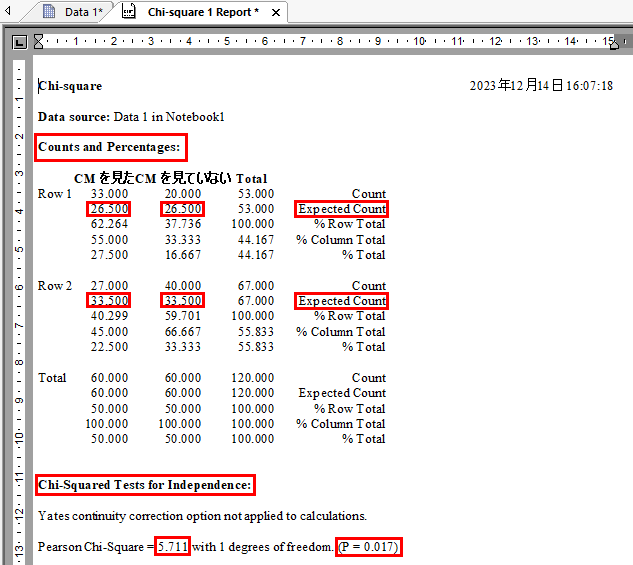
レポートの Counts and Percentages: に Expected Count (期待度数) が表示されます。
Chi-Squared Tests for Independence: にカイ二乗値と P 値が表示されます。
今回、カイ二乗値は 5.711 で P 値は 0.017 です。
P 値が有意水準 α = 0.05 より小さいため、帰無仮説 H0 は棄却され CM の視聴と製品の購入は独立ではない (関連している) という対立仮説が採択されます。
有意水準は Analysis → Options の Power, Use Alpha Value のオプションで指定できます。 有意水準のデフォルトは 0.05 です。
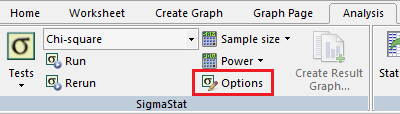
必要に応じて任意の数字に変更し、OK をクリックしてからカイ二乗検定を行います。
カイ二乗検定では、カイ二乗値がカイ二乗分布に従っていることを前提としています。
実際には少しずれる場合があり、そのずれにより有意差が出やすい結果になるリスクを抱えています。
そこで、必要に応じてカイ二乗値の補正を行います。
この補正は統計家のフランク・イェーツ氏の名前が由来で、イェーツの連続性補正や半整数補正などとも呼ばれます。
イェーツの補正を行う場合は、Analysis → Options をクリックします。
Yates Correction Factor (Only for 2x2 contingency tables) を選択します (デフォルトで選択されています) 。
OK をクリックしてから、 Analysis タブ→ Tests → Rates And Proportions → Chi-square... を選択すると、イェーツの補正後のカイ二乗検定のレポートが出力されます。