|
| サイトマップ | |
|
 |
| サイトマップ | |
|
SigmaPlot による記述統計に関する使用例を説明いたします。
記述統計 (Descriptive statistics) は、データの特徴を要約し理解するための方法です。 データの欠損値の確認、中心傾向、ばらつき、および分布の形状などの情報を得ることができます。
SigmaPlot では、統計量やグラフを使用してデータを簡単に要約することができます。次項から、10 名分の身長の計測データ (表1) を例として、各統計値を評価する手順を示します。
| 身長 |
|---|
| 160 |
| 158 |
| 163 |
| 170 |
| 174 |
| 169 |
| 178 |
| 166 |
| 174 |
| 182 |
値の集合に対して最も一般的に使用される統計量は平均値です。
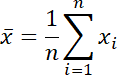
| ※ ※ Σ は i について 1 から n まで合計するという意味です。 |
身長の例のデータについて SigmaPlot を使用して計算します。
SigmaPlot の Σ メニューを選択して New → Worksheet を選択し新規ワークシートを表示します。
ワークシートに次のようにデータを入力します。
記述統計は、Analysis タブ→ Tests → Describe Data → Descriptive Statistics... を選択します。
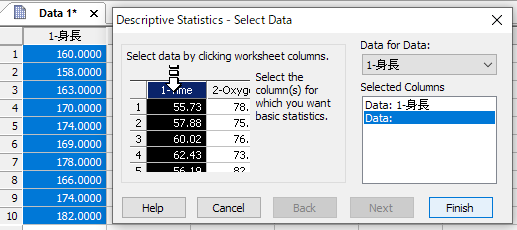
データを選択し Finish ボタンを押します。
SigmaPlot では、Analysis タブ→ Options を選択することで、レポートに計算結果を表示する記述統計の項目を個別に選択することができます。
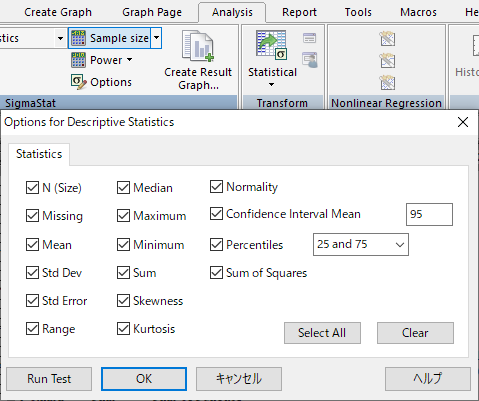
レポートに出力されるすべての計算結果は次のとおりです。
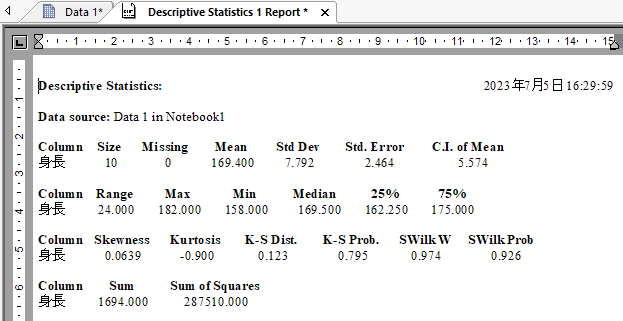
デフォルトでは、小数点以下 3 桁までの値が表示されます。
桁数は Σ メニュー → Options の Worksheet タブで変更できます。
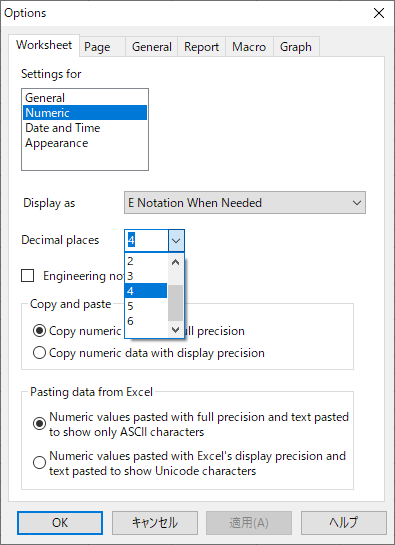
以下は、平均値の結果のみ表示しています。(以降は個別に表示します。)

この値が母集団からサンプリングされたデータの場合は標本平均、母集団のすべてを表す場合は、母平均になります。
データを小さい順に並べてちょうど中央にある値が中央値になります。偶数の場合は、データを小さい順に並べて中央部分の 2 つの値の平均値が中央値です。
身長の例での SigmaPlot の計算結果は次のとおりです。
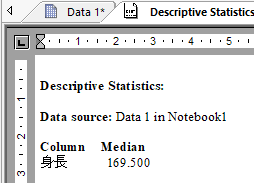
データの個数と最小値、最大値です。SigmaPlot の計算結果は次のとおりです。
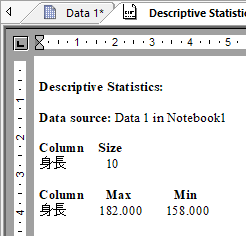
不偏分散と標準偏差は、分布の散らばりの測度として最もよく使用されます。不偏分散は、次の式で求められます。
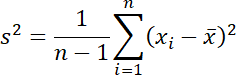
不偏分散の正の平方根を取ることで標準偏差になります。
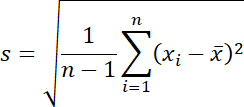
SigmaPlot の計算結果は次のとおりです。
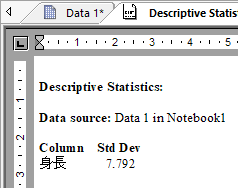
標準誤差は、標本統計量のばらつきを示す指標になります。標本平均や標本比率などの推定値の精度を表します。標本の標準偏差を標本数の平方根で割ったものです。
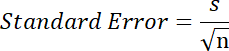
身長の例の標準誤差は、7.792 / √10 = 2.464 になります。
SigmaPlot の計算結果は次のとおりです。
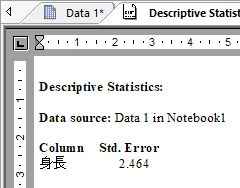
分布が正規分布からどれだけ歪んでいるかを表します。
片側が反対側より値が多くなる傾向で、大まかに左右対称となる分布では歪度はゼロに近くなります。
データが右側に裾が広がっている場合は、歪度は正の値になります。
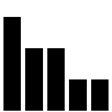
データが左側に裾が広がっている場合は、歪度は負の値になります。
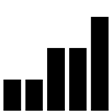
SigmaPlotの計算結果は次のとおりです。
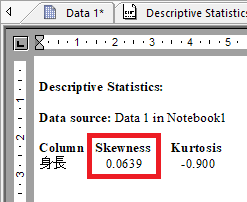
分布が正規分布からどれだけ尖っているかを表します。
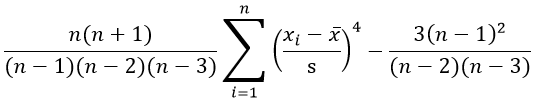
分布が正規分布に比べて急尖の場合は、尖度が正の値になります。

分布が正規分布に比べて緩尖の場合は、尖度が負の値になります。
SigmaPlot の計算結果は次のとおりです。
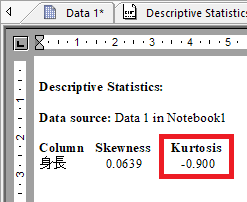
百分位数でデータの上端と下端 (両側) を定義する 2 つのパーセンタイル点です。
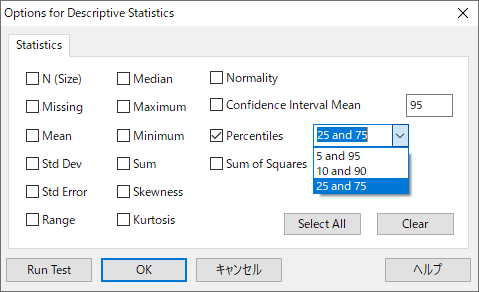
Options で「25 and 75」を選択して得られる計算結果は次のとおりです。
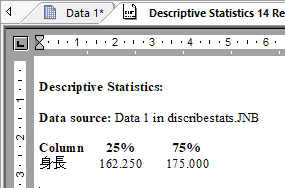
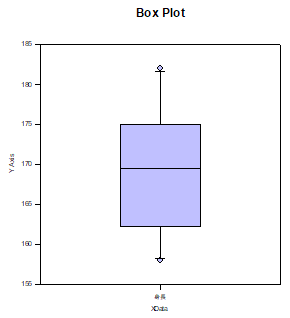
この結果は、箱ひげ図の箱の上側 (75%) と下側 (25%) の値になります。
レポートの余白で右クリックしてメニューから Result Graphs を選択するとグラフを選択できます。
Box Plot を選択して OK クリックすると箱ひげ図が表示されます。
正規性はデータが正規分布に近いかどうかを判断するために使われます。 SigmaPlot では、シャピロ-ウィルク検定またはコルモゴロフ-スミルノフ検定を使ってデータの正規性を評価できます。
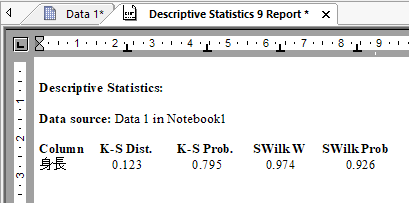
記述統計では、コルモゴロフ-スミルノフ検定とシャピロ-ウィルク検定の統計量及び確率がレポートに出力されます。 個別の正規性の検定の操作 Tests → Normality... を選択することで、有意差の結果を確認できます。
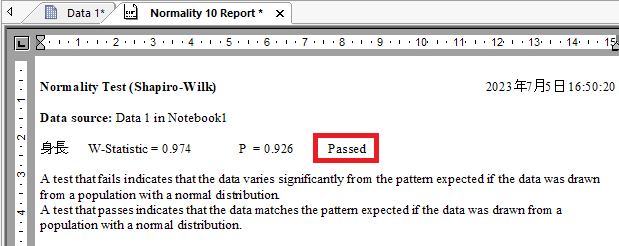
次のとおりいずれも Passed と表示され正規分布であることがわかります。
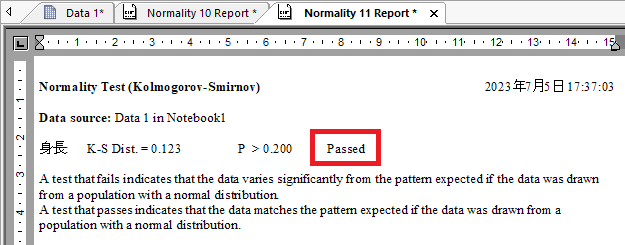
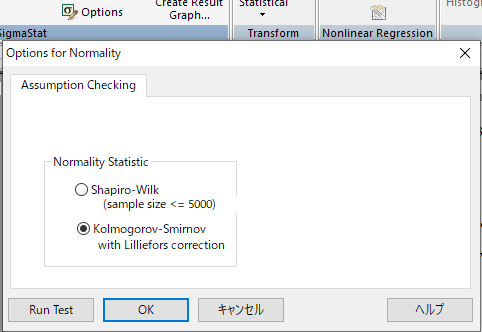
検定手法は Options で指定できます。
平均値の信頼区間は、母集団から抽出されるすべての可能な標本の割合について、真の母集団の平均が収まる範囲です。区間の端点は次の式で与えられます。
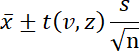
ここで、x バーは平均、 s は標本の標準偏差、 t(v, z) は、自由度 v = n -1 、標準正規パーセンタイル z = 1.96 の t 値です。
95% を入力した信頼区間の計算結果は次のとおりです。
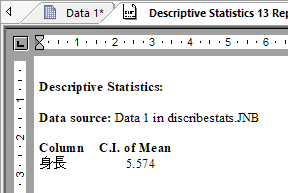
平方和は、データをそれぞれ二乗した合計値です。
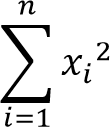
SigmaPlot の計算結果は次のとおりです。
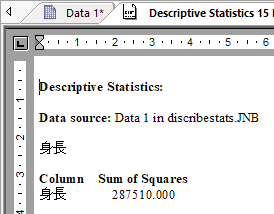
度数分布表は、データ内の値がどのように分布しているかを整理して示すための表です。
度数分布表を求めるには、まず、数値データをカテゴライズする操作を行います。ここでは、身長の数値データを Small、Medium、High の文字データにカテゴライズします。
Analysis タブ → User-Defined... を選択します。
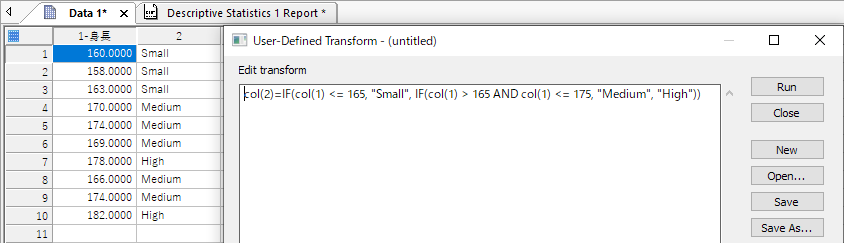
User-Defined Transform ウィンドウの Edit transform に下記を入力して Run を押します。

| col(2)=IF(col(1) <= 165, "Small", IF(col(1) > 165 AND col(1) <= 175, "Medium", "High")) |
165 cm 以下の場合は Small、165cm より大きく 175cm 以下の場合は Medium で、それ以外は High としています。二列目に結果が得られます。
上記で得られたカテゴリデータの度数分布を表示します。
Analysis タブ→ Tests → Describe Data → One Way Frequency Tables... を選択します。
列を選択して Finish を選択します。

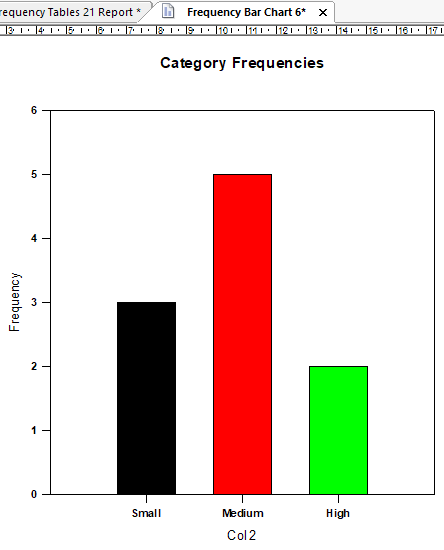
次のとおり、カテゴリデータに関する度数分布表のレポートが得られます。
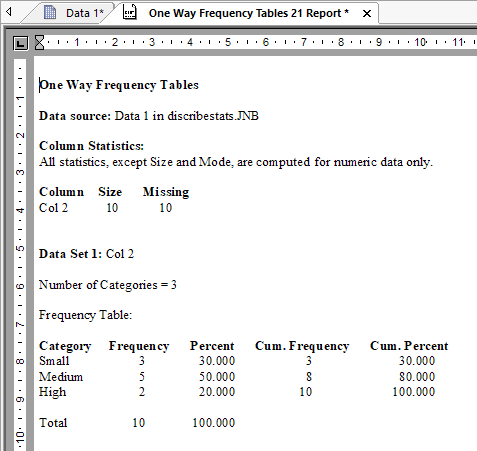
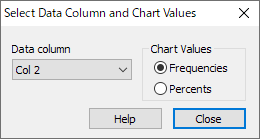
レポートの余白を右クリックし、メニューから Result Graphs を選択して、度数棒グラフを表示できます。
Frequencies (度数) または Percents (パーセント) を選択して Close を押すと度数棒グラフを表示します。