ダブル-ハイブリッド密度汎関数理論

Double-Hybrid Density Functional Theory

• 開発者: Jeng-Da Chai

  Jeng-Da Chai

ダブル-ハイブリッド密度汎関数理論は、MP2 に近い計算コストで化学的精度への接近を大いに期待できます。伝統的な KS-DFT アプローチとは異なり、ダブル-ハイブリッド DFT は、非共有および共有のいずれの系でもうまく動作します。

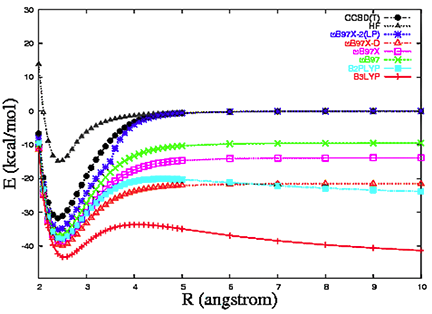
図は、Ar₂⁺ の解離曲線です。いずれの手法も E(Ar) + E(Ar⁺) をゼロ基準としています。

図に示すように、他のハイブリッド（およびダブル-ハイブリッド）密度汎関数と比べると、ωB97X-2 による自己相互作用の誤差は大幅に小さくなっていることがわかります (図は J.-D. Chai and M. Head-Gordon, J. Chem. Phys. 131, 174105 (2009) による)。

論文：

• S. Grimme, “Semiempirical hybrid density functional with perturbative second-order correlation,” J. Chem. Phys. 124, 034108 (2006)
• T. Schwabe and S. Grimme, “Double-hybrid density functionals with long-range dispersion corrections: higher accuracy and extended applicability,” Phys. Chem. Chem. Phys. 9, 3397 (2007)
• Y. Zhang, X. Xu, W. A. Goddard III, " Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics ", PNAS 106, 4963 (2009)
• J.-D. Chai and M. Head-Gordon, " Long-Range Corrected Double-Hybrid Density Functionals ", Phys. 131, 174105 (2009)

Q-Chem 4.0 マニュアル：

• Q-Chem 4.0 User's Manual (開発元：英語)
  この機能の使用法に関する詳しい情報は Q-Chem Manual, Section 4.3.8 をご覧ください。

計算例

• wB97X-2_LP.out
• wB97X-2_TQZ.out