更新日： 14/03/31

基本統計データを使って正規分布を判定

グラフ作成を行う前に、基本統計データを見たいという場合がしばしばあります。Grapher はワークシートのデータについて統計情報を計算し、それらをグラフ化することができます。こうすることによって、データの特性を把握することができます。

この事例で使用するデータは、ここ (サンプルデータ) からダウンロードすることができます。統計情報の計算には、さほど時間を要しません。基本統計データからどのようなモデルを作成するか判断し、箱ヒゲ図とヒストグラムを作成した後、QQ プロットを作ってみましょう。

ワークシートの統計情報

File | Open メニューコマンドをクリックして [random sample.dat] ファイルを開き、開始しましょう。Data | Sort コマンドを使って昇順 (Ascending) に並び替えします。列全体を選択し (反転状態にし) 、Data | Statistics メニューコマンドをクリックします。Statistics ダイアログで、計算したい項目を選択することができます。Minimum、Maximum、Mean、Standard error of the mean、95% confidence interval for the mean、Standard deviation をチェックして下さい。計算結果は、ワークシートに保存するため Copy to worksheet とし Starting in cell の値を C1 に設定します。

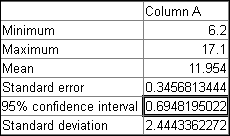**Data** | **Statistics** メニューコマンドで基本統計データを計算・表示させます。

ワークシートにコピーされた表から、データの範囲は 6.2 から 17.1 で平均が 11.954 であることがわかります。平均の 95% 信頼区間は約 0.695。したがって、平均に信頼区間を加えるとその幅は 11.259 から 12.649 になります。すなわち、真の平均 (母平均) は 95％の確率でこの範囲にあることを意味します。標準誤差は、別の信頼区間の計算あるいは検定のために使用されます。標準偏差 2.444 は、値のばらつき具合の推定を表します。これらの値は、仮説検定などのさらに高度な統計解析や、グラフに追加上を加えるために使用されます。

分布を示すグラフを作成

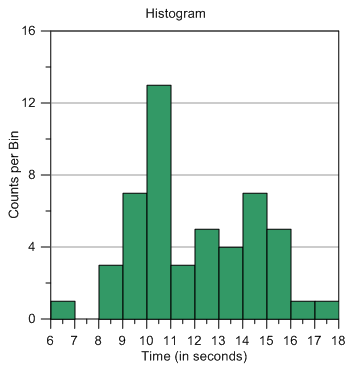
おそらく最初に必要となるグラフは、ヒストグラムでしょう。データ範囲を区分けした各階級のデータポイント数を示すことによって、どのようにデータが分布しているか把握することができます。Grapher では、ビンのサイズは区間幅と同じです。また、ビンの数は任意に設定することができます。

ヒストグラムを作るには、Graph | 2D XY Graphs | Histogram メニューコマンドをクリックします。データファイルを選択して開くボタンを押します。ヒストグラムを作成すると、すべてのデータ (6.2 から 17.1) が含まれる範囲で、ビンのサイズと数が自動的に設定されて表示されます。ビンのサイズと数は、変更することができます。

Object Manager で Histogram 1 を選択します。
Property Manager の Plot タブをクリックします。
スクロールダウンして Number of bins の値を 12 に変更します。
続いて Bin size を 1 にします。

このグラフに、ガウス曲線あるいは既知の分布曲線を当て嵌めてみましょう。このグラフは、正規分布をしているようには見えません。なぜなら、最大ピークが中央からずれており、全体の形も非対称です。そのため、もう少し確率分布について調べてみる必要があります。

ヒストグラムにより、データの範囲と分布の様子がつかめます。

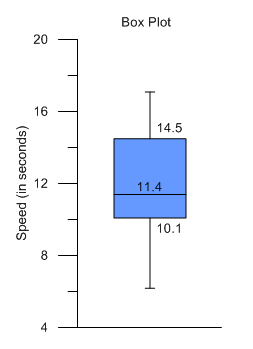
箱ヒゲ図を使うと、生データのばらつきの傾向を素早く把握することができます。箱の本体は中央値の傾向を、そしてヒゲ部分は標準的な値から外れたデータを表します。箱の中の中央値の線を比べることで、データの広がり具合がわかります。

箱ヒゲ図を作るには Graph | Specialty Graphs | Box-Whisker Plot メニューコマンドをクリックします。データファイルを選択し開くボタンを押します。デフォルト設定の箱ヒゲ図が作成されます。箱ヒゲ図は、ラベルや外れ値を追加したり、その他プロパティの値を変更することができます。

ラベルと外れ値を加えます。

Object Manager の Box-Whisker Plot 1 をクリックします。
Property Manager の Labels タブを開きます。
Quartiles (25) セクションを開き、Display にチェックを入れます。
Quartiles (50) セクションを開き、Display にチェックを入れます。
Quartiles (75) セクションを開き、Display にチェックを入れます。
これでグラフ上にラベルが表示されます。Graph | Move Labels メニューコマンドをクリックして、ラベルを移動することができます。ラベルの移動が終わったら、ESC キーをクリックするとラベル移動モードが終了します。
Plot タブを開きます。
Outliers as symbols オプションにチェックを入れます。これにより、ヒゲの範囲外にある外れ値をシンボルで表示できます。
デフォルトの外れ値設定では、何も表示されません。これは、すべての値が 1.5×IQR の範囲に収まっていることを意味しています。IQR は、Quartiles (25) と Quartiles (75) との間の幅を表しています。係数 1.5 は、必要ならもっと小さい値に変更することができます。

箱ヒゲ図は、データのばらつきを中央値、第1四分位 (25％) 、第3四分位 (75％) を使って表しています。

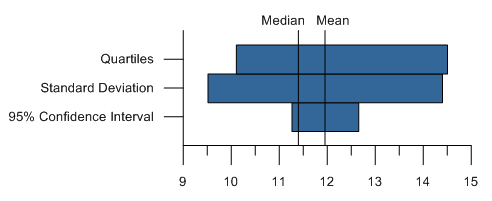
最後に、ワークシートの Data | Statistics メニューコマンドのデータと、箱ヒゲ図の値を比べるグラフを作成します。浮動バーグラフは、データの範囲を表すのに適しています。ワークシートの統計情報をアレンジして、平均値 +95％信頼区間と平均値 -95％信頼区間を別々の列に表示させます。さらに以下の表のように、第1四分位と第3四分位の行と、平均値-標準偏差と平均値+標準偏差の行を追加します。

浮動バーグラフを作るためにデータを再加工します。

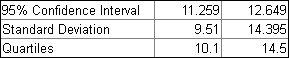浮動バーグラフを作るには、Graph | 2D XY Graphs | Floating Bar メニューコマンドをクリックします。データを選択して開くコマンドをクリックします。デフォルトの状態では、次のように表示されるはずです。

四分位、平均±標準返済、および 95% 信頼区間を示す浮動バーグラフ

QQ プロット

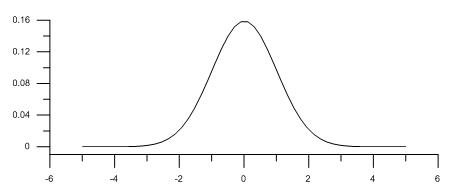
QQプロットは、正規曲線と実データを比較するためのプロットです。直線のフィッティングが行えるデータは、正規分布だと見なせます。まず、実データセットと同じデータポイント数の正規曲線のデータが必要です。適切な間隔の正規曲線は、次のようして描きます。

Grapher の File | Open メニューコマンドでこのグラフを開きます。このグラフは、正規分布関数を使って作成したものです。
正規関数曲線のデータをエクスポートします。
Object Manager で、Normal Distribution Function Plot をクリックします。
調べたいサンプルデータは 50 ポイントですので、この関数から 50 ポイント分をとります。Property Manager の Plot タブをクリックします。Number of points を 50 に変更します。
Graph | Export Plot Data メニューコマンドをクリックすると、新しいワークシートに 50 データポイントがエクスポートされます。
A列 (X値) を選択し、Edit | Copy メニューコマンドをクリックします。
最初の [random sample.dat] データファイルに戻ります。
B1 セルを選択し、Edit | Paste メニューコマンドをクリックします。

QQ プロットを作成するために、Plot ウィンドウをクリックします。

Graph | 2D XY Graphs | Line/Scatter メニューコマンドをクリックします。
random sample ワークシートを選択し開くボタンを押して下さい。
Line/Scatter Plot 1 を選択した上、Property Manager の Plot タブをクリックします。
X column を Column B に変更します。
Y column を Column A に変更します。
曲線の当て嵌めを行うために、Fits の右側にある <Click here to add/edit fits> をクリックします。
ダイアログで Linear のフィット曲線を選択して Add ボタンをクリックし、OK ボタンを押します。
正規分布の値と実際の値の対比図を作成します。

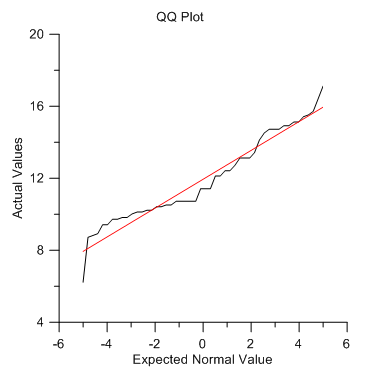線形のフィット曲線にデータがほぼ一致しているため、外れ値はあるもののデータはほぼ正規分布であることがわかります。

結論

基本統計の計算結果とグラフを使って、高度な解析を行うために必要なデータの特性が把握できました。