縦方向の拡大
代数2：計算の前段階 (学習時間：50～80分)

学習目標

このレッスンでは、定数で関数を乗算した場合の影響を理解するための基本的な学習アプローチを紹介します。

数学的目標

• 定数で関数を乗算した時の結果は縦方向に拡大することを理解します。
• 式の変化がグラフに与える影響と、縦方向の拡大についてのその逆を理解します。

技術目標

• Geometry Expressions の機能の特徴に慣れ、変数ツールを使用しダイナミックな学習が出来るようになります。

 

数学の前提知識

• 関数というものが何で、次の３つの基本の関数を理解している必要があります：
  y =x ², y =1/x , y = sin (x)
• 正弦関数で使う弧度法 (ラジアン) が十分に身についている必要があります。
• 関数の表記を理解している必要があります：y =f (x)

 

技術の前提知識

• Geometry Expressions の基本的な知識が必要です。

 

準備するもの

• 学生1名またはペアの学生に対し、Geometry Expressions が動作するコンピューター1台
• 色鉛筆 (あれば)

 

概要 (教師用)

このレッスンでは、3つの関数の縦方向の拡大を視覚的に学習し、関数方程式に定数を掛けることとの相関性を分析します。対話的なソフトウエアの使用により、生徒は自分自身で容易に概念を理解することができます。教師の役割は生徒を促し、脇道にそれないようにすることです。生徒には、正確にパターンを理解したという確証が必要かもしれません。各自の作業のために、事前に用意したモデリングが大きな助けになる、という点がカギです。

パートBは、Geometry Expressions なしで行う必要がありますので、別の紙にコピー して生徒に渡し、生徒をコンピューターから離れさせます。色鉛筆は、グラフの変化を色分けするのに役に立ちます。これは、生徒が容易に理解できるためと、チェック／成績付けを容易にするために、推奨します。クラスによっては、このレッスンは何度も繰り返す必要がある可能性もありますので、特定の生徒のグループに対しては、適宜、内容を修正したり、短くしたりする必要があります。

 

縦方向の拡大 パートＡ

1. 教師はこの時点でアニメーションツールを使用しても構いません。
   
   
   
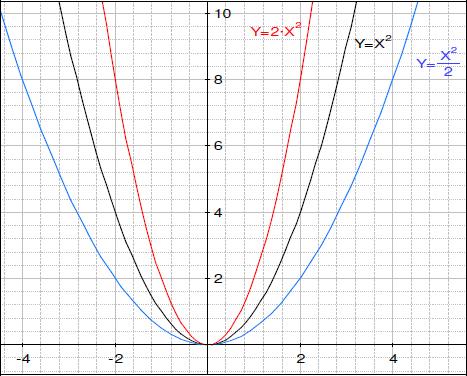
2. 答えはいくつかのバリエーションがあります。a が増加すると、グラフは垂直に引っ張られます (拡大する) 。
   一部の生徒はその代わりに、これを水平方向の収縮と言うでしょう。それは実際、この関数においては正確です。生徒が正弦曲線を調べる時、水平方法と垂直方向の拡大は明確になります。

生徒と議論すると良い点は、彼らの作業中に a = 0 の時何が起こるか、問いかけることです。彼らは代数的に、x 軸と一致する関数方程式 y = 0 を作成することができます。これは a が -2 から 2 まで変化できるようにすることで、パターンの残りの部分がどのように変化するか非常にはっきりと見ることができ、スクロールバー (アニメーション機能) を使用したり、簡単にカーブをある点にドラッグ (移動) することができます。これは、作業の全体のパターンのダイナミックな見方と共に、特定の答えを問題に関連付けることができます。

3. A, B, C)
   D) 答えはいくつかのバリエーションがあります。x 軸上の反射 ― -1を掛けると、垂直方向にグラフが反転します。他の負の数を掛けると、反射と縦方向の拡大が見られます。
   
   
   
4. 
   
   
   
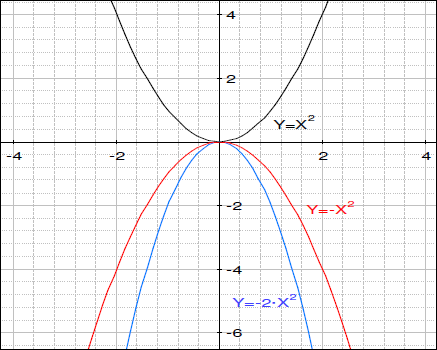
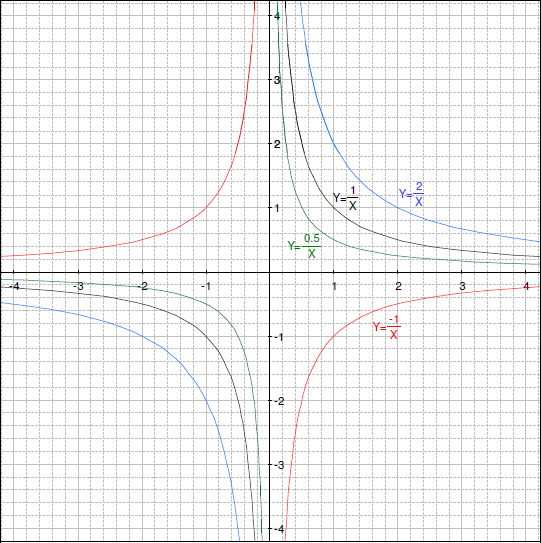
5. 答えはいくつかのバリエーションがあります。定数 a を掛けると、縦方向にグラフが拡大されます。a が負の場合、グラフは x 軸を横切って反射され拡大されます。
   
   
6. 
   
   
   
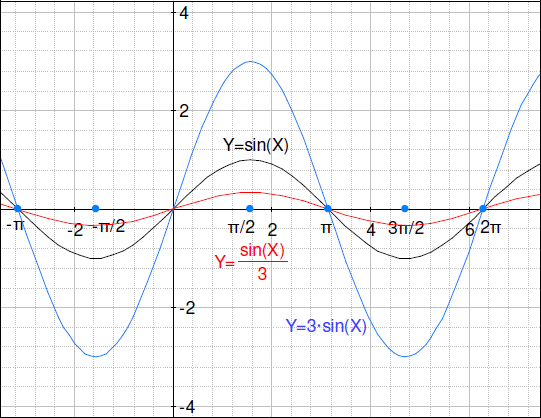
7. a で関数を乗算すると、a を係数として垂直方向に引き延ばされます (垂直方向の拡大) 。
   
   
8. 答えは様々なバリエーションがあります。一つの可能性は：
   
   
   
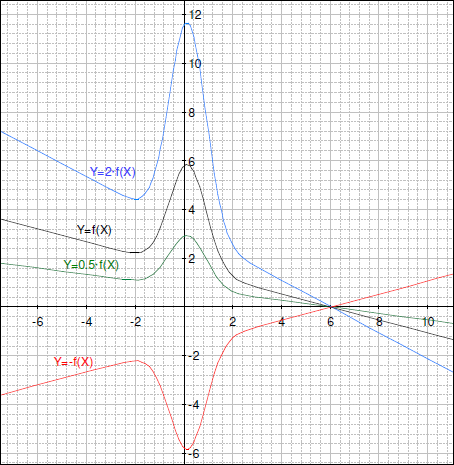
9. A)
   a の係数による垂直方向の引き延ばしまたは垂直方向の拡大。
   
   B)
   • a > 1 ならば、グラフは垂直に高く伸びる
   • a < 1 ならば、グラフはひっくり返される－x 軸を挟んで反射－そして拡大または伸縮
   • 0 < a < 1 ならば、グラフは垂直に縮む－より短くなる

教師のモデリング

コンピューター学習から自習に生徒を移行させるときに、垂直方向の拡大を黒板で説明 (モデリング) したいと思うかもしれません。問題は、生徒が一般的な図形を非常にラフに描くかもしれないということです。彼らが特定の点を見て、指定された係数で y の値を乗算する必要があるということをモデル化してください。特に、参照点として拡大する相対的な最大値と最小値を特定する例を与えて、曲線をモデル化することもできます。また、生徒にも x 軸上のどんな点もそこにとどまるということを認識させてください。

 

---

縦方向の拡大パートＢ (生徒に配布する部分です)

1. & 2.
   

3. - 5.
   

6. - 7.
   
   
   

8. h(x) = 1/2 * j(x)
   j(x) = 2* h(x)
   
   
9. k(x) = 4 * m(x)
   m(x) = 1/4* k(x)

---

 

縦方向の拡大パートＡ

I. y = x²

1. 下に関数のグラフを描いてください。これらの関数はすべて同じファミリーのメンバーで、y = x² が親関数です。Geometry Expressions の描画ツール を使って方程式を入力します。この際、乗算を示すために * 、指数を示すために ^ を使う必要があります。
   
   A) y =x²
   B) y =2x²
   C) y =1/2x²
   
   
   さて、係数 (変数の前の数字) の変化で何が起こるのか決定してみてください。y = ax² のグラフを描くために、Geometry Expressions の機能ツールを使います。曲線をクリックしたり、上下にドラッグすることでグラフがどのように変化するかを見ることができます。また、変数ツールパネルで a をハイライトしてスクロールバーをドラッグするとグラフはどうなるでしょうか。少なくとも 0 から 5 までの値で調査してみましょう。値を大きくする (すなわち親関数により多くの数をかける) と、どのようなグラフになりますか？
   
   
2. 次の２つの関数のグラフを描いてください。y = ax² のグラフを使って、負の数を掛けた時、関数に何が起こるかをみてみましょう。
   
   A) y =x²
   B) y =(-1)x²
   C) y =(-2)x²
   D) -5 から 5 までの値を調べるためにスクロールバーを使います。関数に負の数をかけるとどのようになりますか？
   
   

 

Ⅱ. y =1/x

3. ここでは、y =1/x について同じような問題を学習します。Geometry Expressions で新しいグラフ y =a/x を描きます。これは親関数に定数 a かけたものであることに注意してください。グラフを作成するために a に異なる値を割り当てます。それぞれの関数を色分けしたり、ラベルをつけましょう。また、もっと詳しく理解するために変数ツールパネルでスクロールバーを使ってみましょう。
   
   A) y =1/x
   B) y =2/x
   C) y =0.5/x
   D) y =-1/x
   
   
   
   
4. 親関数に定数 a をかけるとどのような影響がありますか？a が負の値のときはどうですか？

 

Ⅲ. y = Sin(x)

5. Geometry Expressionsで、新しく y = a*sin(x) のグラフを描きます。プログラムをラジアンモードに設定します (編集 / 初期設定 / 数学 / 数学 / 角度 モード → ラジアン) 。グラフを作成するために異なる値を割り当てます。Geometry Expressions のグラフは、π, 2π などのラベルを持っていません。関数を色分けしたり、ラベルをつけましょう。また、a が変わることの影響をもっと詳しく理解するために変数ツールパネルでスクロールバーを使ってみましょう。
   
   A) y=sin(x)
   B) y=3sin(x)
   C) y=1/3sin(x)
   
   
   
   
6. この関数に定数をかけると、グラフにどのような影響がありますか？

 

Ⅳ. Y =一般的な関数

7. ここでは、任意の関数に定数を掛けた結果を調べましょう。Geometry Expressions で新しく y = f(x), y = g(x) or y = h(x) のグラフを描きます。あなたの隣の人のグラフと違うものになるように、何回かクリックしてドラッグしてみてください。ここでグラフは、y = a*f(x) [または a*g(x) など] となっています。スクロールバーで a の値を変えると何が起こるか見てみましょう。下に4つのグラフを描き、ラベルを付けまし� �う。親関数と3つの異なる a の値、a > 1、a > 0、0 < a < 1 をかけたものです。
   
   
   
8. ここまでで、関数に定数をかけることで、どんな関数でも同じように変化することがわかったと思います。確信が持てない場合には、戻って4つの関数についてもう一度確認してみましょう。
   
   A) 一般的な言葉で説明してください。定数 a をかけることによって関数にはどのように影響しますか？
   B) a の値の違いでの影響についてより具体的に説明してください。
   • a > 1
   • a < 0
   • 0 < a < 1

 

---

縦方向の拡大パートＢ (学生に配布する部分です)

次の問題は、コンピューターの助けなしに行わなければなりません。パート A を参照して考えてください。それぞれの問題では、縮尺と特定のキーとなる点に注意を払ってください。漠然とスケッチしてはいけません。

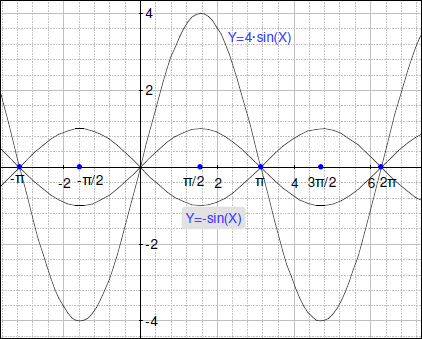
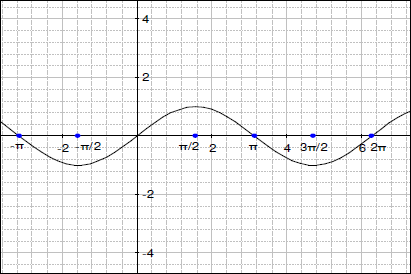
1. 下には関数 y =sin(x) のグラフがあります。同じ軸で、y=4*sin(x) のグラフを描いてください。
   
   
2. また、y=(-1)*sin(x) のグラフを描いてみましょう。
   
   
   
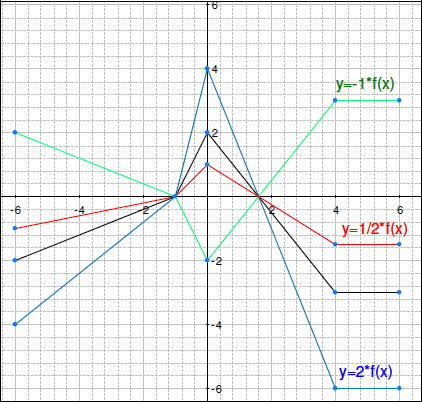
3. 下には y = f(x) のグラフがあります。同じ軸で、y = f(x)+2 のグラフを描いてください。描いたグラフにラベルを付けるか、色分けしてください。
   
   
   
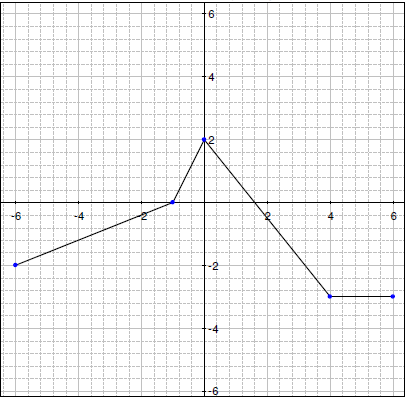
4. 次に y =½ * f(x) のグラフを描いてみましょう。
   
   
5. さらに、関数 y = -1*f(x) のグラフを描いてみましょう。
   
   
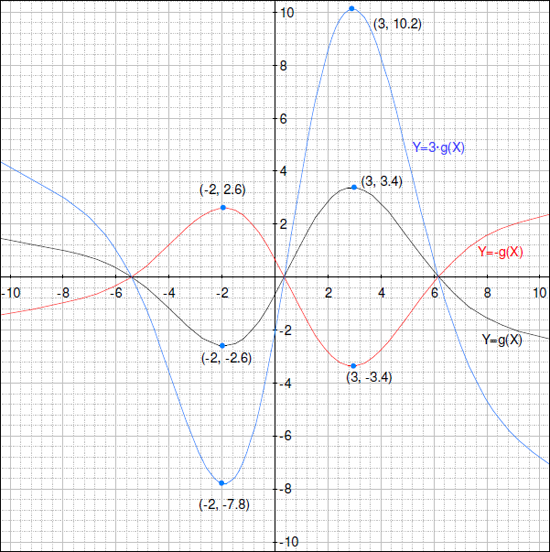
6. 下には関数 y = g(x) のグラフがあります。同じ軸で、y = 3 * g(x) のグラフを描いてください。
   
   
   
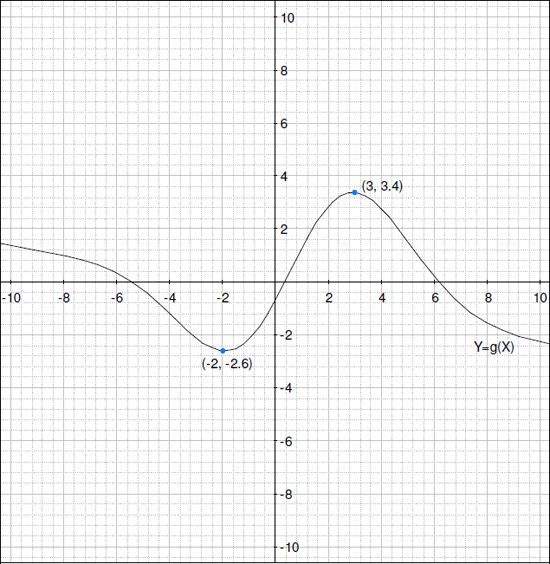
7. 次に、関数 y = -1*g(x) のグラフを描いてみましょう。グラフにラベルを付けるか、色分けしてください。
   
   
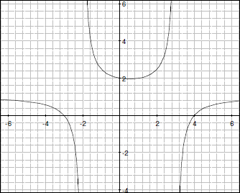
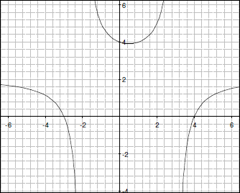
8. 下には互いにシンプルな関係のある2つの機能 h(x) と j(x) のグラフがあります。１つは垂直方向の拡大です。下の式の空欄を埋めてその２つの関係性を書き出してみてください。
   
   h(x) = ______ * j(x)
   j(x) = ______ * h(x)
   
   

   y = h(x)	y = j(x)

   
   
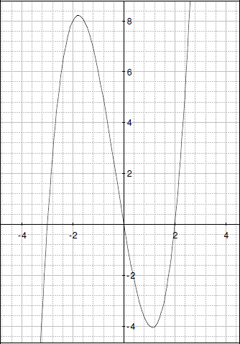
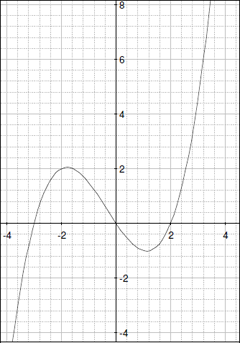
9. 互いにシンプルな関係のある２つの関数 k(x) と m(x) のグラフがあります。２つの方程式を書くことによって２つの方法で関係を書き出してみてください。
   
   k(x) =
   m(x) =
   
   

   y = k(x)	y = m(x)