単位円入門 (学習時間:約50分)
学習目標
このレッスンでは、直角三角形の三角法の理解、単位円と角度が 90° 以上、または 0° 以下の三角比の理解へと移ることを意図しています。正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) の定義の詳細だけではなく、直角三角形と単位円との間の明確な概念的関連性があることを理解していきます。
数学的目標
- 直角三角形の三角法と単位円上の点の座標との関連性を学びます。
- 90° 以上、0° 以下の角度に関する正弦・余弦・正接の詳細な定義を理解し、活用できるようになります。
技術目標
- Geometry Expressions プログラム上で、描画、制約、アニメーション作成、軌跡の作図を含む、様々なツールの利用を学習します。
数学の前提知識
- 直角三角形の三角法を十分に理解している必要があります。
- 四象限直交座標系 (デカルト座標系) を理解している必要があります。
技術の前提知識
- Geometry Expressions に関する知識と経験がほとんどなくても、このレッスンを完了させることが出来ます。
準備するもの
- 学生1名、もしくは1組のペアの学生に対し、Geometry Expressions が動作するコンピューター1台
- 関数電卓 (あれば)
概要 (教師用)
このレッスンは、直角三角形に限定されている三角法の理解から、単位円の理解へと導きます。これは、三角法の2つの側面である論理的な結合と部分的な等価性を強く重視した方法で行われます。またこのレッスンでは、多くの学生が、自分で取り組まなくてはいけません。教師の指示があまり必要ないように構成されています。しかし、いくつかの把握すべき一般的な課題は、以下の通りです。
このレッスンでは、書く作業が少なく、ほとんどの作業をコンピューター上で行います。学生の取り組みを画面上で確認し、一連のチェック項目を設定したり、レポートを初期段階で確認する必要も出てくるでしょう。その場合は、ステップ 8、14、16 を推奨します。また、この種の問題は容易に入手できるので、自習問題は含まれていません。ここから始まるレッスンで、学生が取り組まなくてはならない問題は (ワークシートもしくはその他の方法で) 、以下の通りです。
- 回転角度の設定された単位円上の点の座標を特定する
- 四象限における正弦 (サイン) と余弦 (コサイン) の符号を特定する
- それぞれの三角関数値に単位円上の点の座標を関連付ける
ステップ 1-5: Geometry Expressions の初期のバージョンでは、軸に対してダイレクトに、または座標を通じて C 点を制約して三角形を構築すると、制約に関する矛盾が起こりやすくなっていました。C の位置が、0° の傾き、または 0° の方向として設定された場合は、このような問題を避けることができます。最近のバージョンでは、このような問題は起こりません。
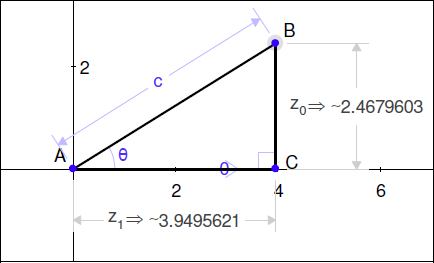
ステップ 8 まで完了すると、学生が書いた図は、次のようになっているはずです (数字は、選択した角度測定と C の長さによって異なります) 。
ステップ 14 :B 点の座標との等価性を把握したのち、学生は辺の長さの測定を削除したいはずです。削除して、図を整理することは問題ありません。
ステップ 16 :軌跡を作図するためのデフォルトの変数は c ですが、θ が必要です。学生が円の代わりに直線を取得した場合には、変数 θ を選択させてください。
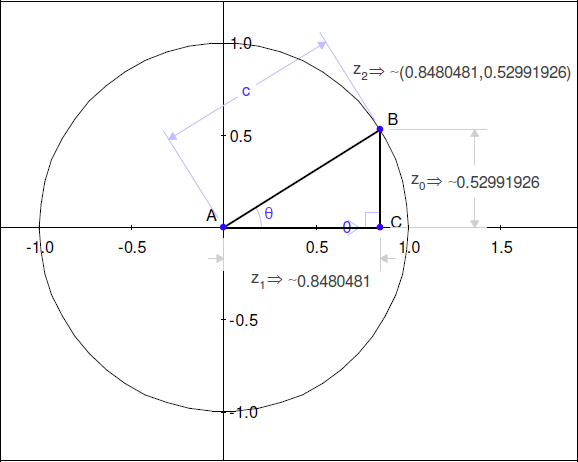
最終的な図は、次のようになります。
※ 次ページ以降が学生に配布する部分です。
単位円三角法入門
始める前に:
新しい Geometry Expressions ファイルを開きます。必ず度数法モードになっていて、軸を表示していることを確認します (編集 ⇒ 環境設定 ⇒ 計算 ⇒ 計算 ⇒ 角度モード → [度]。上部ツールバーの軸/グリッドボタン  をトグルする) 。
をトグルする) 。
直角三角形:
- 10~80 の数を選び、ここに記入しましょう⇒ _______________
- 第1象限に三角形を作成しましょう。[線分 / draw line segment]
 を使って、第1象限に A を起点として、B と C を頂点とする三角形 ABC を作成します。
を使って、第1象限に A を起点として、B と C を頂点とする三角形 ABC を作成します。
- 辺 AC をハイライトし、[傾き / constrain slope]
 を使って、傾きをゼロに設定してください。すると、辺が X 軸上になります。
を使って、傾きをゼロに設定してください。すると、辺が X 軸上になります。
- Shift キーを押しながら、辺 BC と辺 AC を同時にハイライトします。[垂直 / Constrain perpendicular]
 を使って、直角を作ります。
を使って、直角を作ります。
- 辺 AB と辺 AC を同時にハイライトし、[角度 / constrain angle]
 を使って、θ の角度に制約をかけます。
を使って、θ の角度に制約をかけます。
標準位置に直角三角形を作成しました。標準位置にある直角三角形は、原点に関心のある角度 (θ) を持つ頂点を持ち、正の X 軸上に三角形の1つの辺をもち、第1象限に3番目の頂点があります。どのような直角三角形も、回転、変換、さらには反転することでこの形にできることを覚えておきましょう。
- 辺 AB をハイライトし、その長さを変数 c とするための長さ測定に、[距離/長さ / constrain distance]
 を使います。
を使います。
- これで三角形が作成できました。変数ツールのパネルを開き、θ をハイライトしましょう。次に、下のボックスに最初に選択した数を入力しましょう。また数字の隣にある
 アイコンをクリックして、θ を固定します。
アイコンをクリックして、θ を固定します。
- [距離/長さ / calculate real distance]
 を使って、作った三角形の a と b の長さを測定しましょう。c の長さは、変数ウィンドウに表示されています。測定した長さを使って、正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) の値を記入しましょう。
を使って、作った三角形の a と b の長さを測定しましょう。c の長さは、変数ウィンドウに表示されています。測定した長さを使って、正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) の値を記入しましょう。
| |
比 |
実数 |
| 正弦 (サイン) (θ) |
/ |
|
| 余弦 (コサイン) (θ) |
/ |
|
| 正接 (タンジェント) (θ) |
/ |
|
- 関数電卓の三角関数を使い、比率を確認します。その際、電卓が度数法モードになっているか確認しましょう。
- c の長さを変更すると、三角形にはどのようなことが起こるでしょうか。変数ツールパネルの c をハイライトし、数値を変更して、Geometry Expressions で試してみましょう。数値をキーボード入力するか、下に表示されるスクロールバーを使って c の長さを変更することが出来ます。
- 三角比にどのようなことが起こりましたか?
- 残りの演習として、c の長さを 1 にし、変数ツールパネルで固定しましょう。必要であれば、画面上のツールバーの「拡大」ボタン
 で、図を拡大して使ってください。
で、図を拡大して使ってください。
- 頂点 B の場所を特定するために、B をハイライトし、[座標 / calculate real coordinates]
 をクリックしてください。そしてステップ 8 で計算した結果と比べてください。どのような事に気付きましたか?
をクリックしてください。そしてステップ 8 で計算した結果と比べてください。どのような事に気付きましたか?
- では、θ のロックを解除し (アイコンを再度クリック) 、いくつか他の角度を試してみましましょう。そして変数ツールパネルを使ったり、図の中の頂点Bをクリックやドラッグしてみましょう。2つの異なる角度に対する三角比が頂点 B に対する座標と一致するかどうかを調べてみましょう。
| θ |
B の座標 |
Cos(θ) |
Sin(θ) |
| |
( , ) |
|
|
| |
( , ) |
|
|
| |
( , ) |
|
|
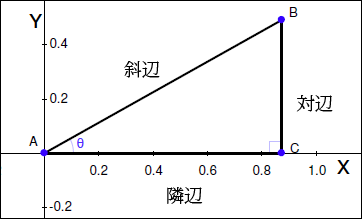
なぜこのような結果となるのでしょうか?直角三角形が標準位置にある場合、対辺の長さは、頂点 B の y 座標に等しく、隣辺の長さは、x 座標と等しいと言えます。
また、先ほど三角形を設定したように、斜辺は常に 1 になります。これは、辺の比を変えることなく直角三角形に当てはめることが出来ます。
したがって
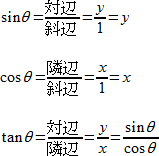
これらの事実は、90° 以上や、0° 以下の角度に対する正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) の定義をさらに深めるために使うことができます。
- θ の全ての可能な値を見てみましょう。これを行うためには、変数ツールパネル上で θ をハイライトし、そのセクションの一番下アニメションツールを使ってみます。
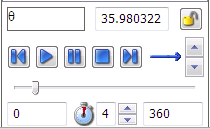 このツールで、与えられた変数の値の範囲を連続的に移動させることができます。左下と右下のボックスは、θ の最小値と最大値を示しています。0° から 360° の変化を見てみます。手動で値を変えたり、スクロールバーをドラッグしたり、再生ボタンをクリックすることで自動的にコンピューターに操作させることもできます。頂点 B の軌跡に注目してください。
このツールで、与えられた変数の値の範囲を連続的に移動させることができます。左下と右下のボックスは、θ の最小値と最大値を示しています。0° から 360° の変化を見てみます。手動で値を変えたり、スクロールバーをドラッグしたり、再生ボタンをクリックすることで自動的にコンピューターに操作させることもできます。頂点 B の軌跡に注目してください。
- 軌跡をより明確に表示させるために、頂点 B をハイライトさせ、[軌跡/construct locus] ツール
 を使いましょう。ポップアップメニューが表示されるので、θ の変数を設定しましょう。開始値を 0、終了値を 360 に設定し、OK をクリックします。そしてステップ 15 の操作からアニメーションを繰り返します。
を使いましょう。ポップアップメニューが表示されるので、θ の変数を設定しましょう。開始値を 0、終了値を 360 に設定し、OK をクリックします。そしてステップ 15 の操作からアニメーションを繰り返します。
直角三角形のあらゆる可能性である、値を 0° から 90° とした時、頂点 B は弧を作ります。三角形の範囲を超えてこのパターンを繰り返すと、起点を中心とした円、単位円を作図することになります。θ が正の x 軸で形成された角度である時、B の座標は (cosθ, sinθ) 、となります。このトリックは、θ を少し別の角度から考えるとわかるでしょう。直角三角形の鋭角であるとする代わりに、θ をアニメーションにおいて x 軸から離れる、点 B が回転した角度としてとらえてみましょう。0° から 90° の値の場合、これらの2つの θ の定義は全く同じです。しかし、次の定義は 90° 以上の角度を使うことになります。
- 同じように、0° 以下の角度は反対方向への回転を示します。変数メニューの最初の値を -360° に変更してみましょう。スクロールバーを使って動きを見てみましょう。
簡単に言うと、正弦と余弦の詳しい定義は、正の x 軸から時計回りに θ° 回転した後の、単位円上の座標です。座標は (cosθ, sinθ) です。同様に、θ の正接は y/x です。
- 別の象限の様々な角度でアニメーションを一時停止してみましょう。正弦が正と負、または余弦が正と負の場合の座標から確定してみましょう。用語 “正” と “負” で、以下の表を完成させましょう。
【図の中のPoritive=>正】
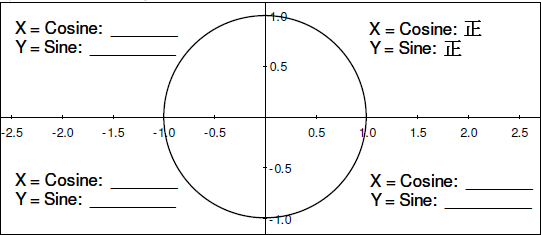
- これまでに学習した中で、または単位円上の点を観察することで、角度 θ の正弦は、どのような最大値と最小値を持ちますか?これが正弦の値の範囲です。
- 角度 θ の余弦に、最大値と最小値として同様な答えが導き出せますか?これが余弦の値の範囲です。


![]() をトグルする) 。
をトグルする) 。 で、図を拡大して使ってください。
で、図を拡大して使ってください。
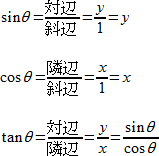
 このツールで、与えられた変数の値の範囲を連続的に移動させることができます。左下と右下のボックスは、θ の最小値と最大値を示しています。0° から 360° の変化を見てみます。手動で値を変えたり、スクロールバーをドラッグしたり、再生ボタンをクリックすることで自動的にコンピューターに操作させることもできます。頂点 B の軌跡に注目してください。
このツールで、与えられた変数の値の範囲を連続的に移動させることができます。左下と右下のボックスは、θ の最小値と最大値を示しています。0° から 360° の変化を見てみます。手動で値を変えたり、スクロールバーをドラッグしたり、再生ボタンをクリックすることで自動的にコンピューターに操作させることもできます。頂点 B の軌跡に注目してください。