直角三角形と三角法 (学習時間：約30分)
学習目標
このレッスンを通じて、三角比の原則について理解を高めることができます。相似三角形に関する予備知識から、当量比を発見しながら、正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) の正式な定義を確実に組み立てていきます。
数学的目標
- 基本的な直角三角形を使って、正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) を学びます。
- 相似三角形に関する三角比と予備知識のつながりを理解します。
技術目標
- Geometry Expressions を使って指示された鋭角の直角三角形を作成します。
数学の前提知識
- 何が相似三角形とそれらの辺の比率性を構成するのかについて学びます。
技術の前提知識
- なし。Geometry Expressions に関する基礎知識は役立ちますが、必須ではありません。
準備するもの
- 学生１名、もしくは１組のペアの学生に対し、Geometry Expressions が動作するコンピューター１台
- 関数電卓１台
概要 (教師用)
このレッスンは入門編であり、全てをカバーするわけではありません。学生が、相似直角三角形のある比率を、正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) の名称を持つことを理解する基礎を作るものです。直線定規と分度器を使用する大変一般的な課題ですが、パターンを見るには学生の作図の精度は必ずしも高いものではありません。例えば、特定の角度の正弦 (サイン) の計算値には大きな変動の可能性があります。Geometry Expressionsを使うことで、精度を高めます。
- すべての三角形は同じ形状である必要がありますが、サイズが異なります。すなわち、相似していなければいけません。
- 学生の回答は様々になる可能性がありますが、4、5、6 行目では、それぞれ４つのすべてのコラムにおいて、同じ回答になる必要があります。これらは、学生が選択した角度の正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) に対応している必要があります。
- 学生の回答は全ての行において同じでなければなりません。
- 角度-角度の類似則。これは少人数のグループディスカッションでの課題に向いています。学生には、この定理と、その他の想定できる範囲で相似則についてレビューさせましょう。学生が相似則について学習したことがないのであれば、これは相似についての予備説明となり、より一般的な用語で相似についてのディスカッションをすることができます。
- 多様な回答が出ることでしょう。
この時点では、学生には語彙についてのサポートが必要であり、また同時に自主的な演習も必要です。このような演習は、ほぼすべての代数のテキストに掲載されているので、ここでは繰り返しません。推奨される演習には以下のようなものがあります：
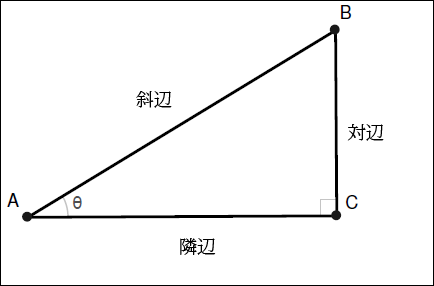
- 直角三角形と角度を示し、どれが「対辺」、「隣辺」、「斜辺」であるかを回答させます。様々な回転方向を使います。
- 直角三角形と3つの辺を示し、2つの鋭角に対する正弦 (サイン) ・余弦 (コサイン) ・正接 (タンジェント) の三角比を回答させます。
- 計算機を使い、指定された角度の正弦・余弦・正接の三角比を計算させます。
- 直角三角形、3つの辺、そして三角比を示し、与えられた角度の正弦・余弦・正接を計算させます。
※ 次ページ以降が学生に配布する部分です。
入門：直角三角形と三角法
10 ～ 80 の数を選び、ここに記入しましょう ⇒ ___________
- Geometry Expressionsで、[ファイル] ⇒ [新規作成] を選択
- [編集] ⇒ [環境設定] ⇒ [計算] ⇒ [計算] ⇒ [角度モード] を [度] に設定
- [表示] ⇒ [軸]
- あなたが指定した数値と同じ値の角度を持つ、直角三角形を作図
- 三角形 ABC を描くためには、[線分 / Draw line segment]
もしくは [多角形 / Draw polygon] 
を使います。
- 角度 C を選択し (Shift キーを押しながら、辺 AC をクリックし、そのまま辺 BC をクリック) 、[垂直 / Constrain perpendicular]
を選択します。
- 角度 A を選択し、[角度 / Constrain angle]
を選択。角度を最初にあなたが指定した数値と同様の数値になるように設定しましょう。
- AB をハイライトし、[距離/長さ / Calculate real distance]
を選択します。「Z0 ⇒」と値が表示されます。Z1 と Z2 となる辺 BC および AC を繰り返しましょう。具体的な数字は右の「変数」に表示されます。
- どれかの頂点をドラッグしましょう。三角形のサイズと形で気付くことは何ですか？
- 4つの異なるバージョンの三角形を作り、次の表を完成させましょう。ただし、すべてにおいてあなたが最初に指定した角度を使わなければなりません。三角比を求めたら、1/1000 の桁まで記入しましょう。
|
|
三角形１ |
三角形２ |
三角形３ |
三角形４ |
| 1 |
長さAB |
|
|
|
|
| 2 |
長さAC |
|
|
|
|
| 3 |
長さBC |
|
|
|
|
| 4 |
BC/AB |
|
|
|
|
| 5 |
AC/AB |
|
|
|
|
| 6 |
AC/AB |
|
|
|
|
- あなたは、項目 4～6 で何か気付いた点はありますか？
- なぜ、頂点 C が直角で、頂点Aがあなたの選んだ角度のを持つすべての三角形が相似であると言えるのでしょうか（つまり、それぞれの三角形はすべて他のスケールモデルです）？
指定された角度を持つ直角三角形はすべて相似であるため、辺の比は等しくなります。これが、最後の３項目で確認できたことです。三角法はすべて、相似する三角形と等比という事実に基づいています。直角三角形の辺の比には、非常にたくさんの用途があるので、数学者がこれらに名前をつけました。
- 項目4／正弦（サイン）：斜辺と対辺の比
- 項目5／余弦（コサイン）：斜辺と隣辺の比
- 項目6／正接（タンジェント）：隣辺と対辺の比
- あなたが選んだ角度の正弦・余弦・正接を電卓を使って計算しましょう。そして、表で値を比較しましょう。
正弦（サイン）：
余弦（コサイン）：
正接（タンジェント）：
