Gaussian 16 ベンチマーク結果

はじめに

Gaussian 16 Rev. A.03 (Gaussian 16) および Gaussian 09 Rev. E. 01 (Gaussian 09) にて、SMP並列に 用いるコア数を変えて力の計算を実行し、以下の 2つの観点から比較しました。力の計算の計算時間は、構造最適化の 1ステップにかかる計算時間の見積もりに用いられます。

• ％NProcShared と %CPU キーワードの計算時間の比較
  Gaussian16 から新しく追加された %CPU キーワードを、従来の %NProcShared (%NProc) と比較しました。どちらのキーワードも SMP 並列で使用する並列コア数を指定しますが、新しい%CPU では特定のスレッドを特定のコアに紐づけて計算します。
  ※ Gaussian 16 では %CPU の利用が推奨されます
  
  
• Gaussian 16 と Gaussian 09 の計算時間の比較
  同じ条件で Gaussian 16 および Gaussian 09 による計算を実行し比較しました。

 

計算方法

コカイン (図1) に対して、B3LYP/6-311++G(df,p) レベルで力の計算を実行しました。並列処理を行わない場合と、SMP 並列に用いるコア数を 2 ,4, 8, 16 コアと変えた場合で計算し、それぞれ 1コアにつき 800MB のメモリを割り当てました。Gaussian 16 では 2電子積分の精度に関するデフォルト設定がより高精度になったため、Gaussian 09 を実行するためのインプットにはIntegral=(UltraFine,Acc2E=12) キーワードを追加して、計算条件を一致させました。Gaussian およびマシンの情報は、表1 にまとめました。

図 1　コカイン (左：3次元構造 (GaussView 6) 、
右：2次元構造 (ChemDraw Professional 16.0) )

 

表 1　今回用いた Gaussian およびマシンの情報

Gaussian バイナリ 情報 Gaussian 16 Rev. A.03, x86_64 (AVX2 enabled) Gaussian 09 Rev. E.01, x86_64 (AVX enabled) CPU インテル® Xeon® プロセッサー E5-2630 v3, (8 コア, 2.40GHz) × 2 コア数 16 コア ( 8コア×2 ) メモリ 64 GB (DDR4-2133, 8GB×8) システムの種類 64bit Linux OS

 

 

結果と考察

SMP 並列処理に用いたコア数を横軸に (並列しない場合を 1 としました) 、計算時間を縦軸にとって、Gaussian 16 で %Nproc を用いた場合を青色、同じく Gaussian 16 で %CPU を用いた場合を赤色、Gaussian 09 を用いた場合を緑色の棒グラフに示しました (図1) 。いずれの結果も SMP 並列に使用するコア数を 2倍に増加すると計算時間がおよそ 45% 短縮しました。

 

図 2　 Gaussian 16 (G16) の ％Nprocshared (％NProc) と％CPU、および Gaussian 09 (G09)
を用いた場合で SMP 並列数を変えたときの力の計算の計算時間

 

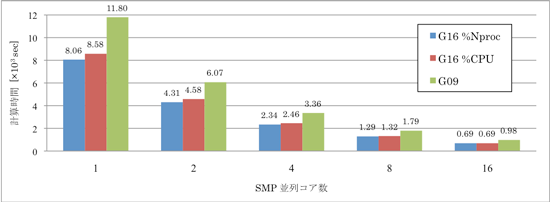まず、Gaussian 16 の %Nproc と %CPU の結果を比較すると、いずれの並列数においても計算時間に大きな違いはみられず、キーワードの違いによるパフォーマンスの違いを確認することはできませんでした。開発元によると、複数のジョブを同時に計算させた場合など、CPU が他に別の処理を実行している場合には、%Nproc のよりも %CPU の計算時間が短縮する可能性があるとのことです。

次に、Gaussian 16 (青色) と Gaussian 09 (緑色) を比較すると、並列数によらず Gaussian 16 の計算時間は Gaussian 09 と比較して 30% 程度短縮していました。そこで時間短縮の理由を調べるために、まずは総計算時間における各計算過程の割合を調べました (図3) 。l502 は SCF 計算を、l703 は力の計算を実行する計算過程です。

 

図 3　Gaussian 16 (G16) および Gaussian 09 (G09) の力の計算において
l502 および l703 に要した時間の割合 (16 並列の場合)

 

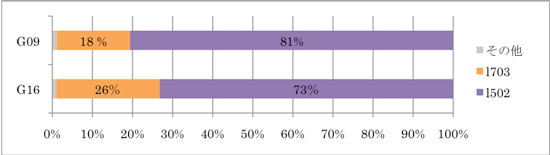Gaussian 16 および Gaussian 09 のどちらの計算時間においても、l502 がおよそ 70～80 %、l703 がおよそ 30 ～20 %と、l502 および l703 による計算過程が大部分を占めていました。図3 は 16 並列計算の場合ですが、並列数が変わっても l502 と l703 が総計算時間の大部分を占める傾向が確認できました。

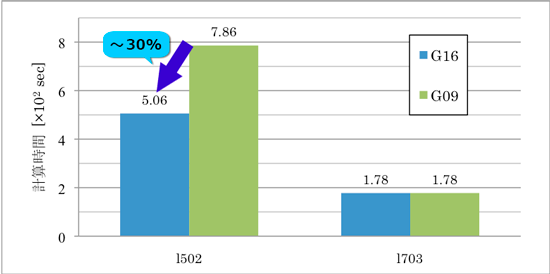
そこで、このときの l502 および l703 に用いた時間を Gaussian 16 と Gaussian 09 で比較しました (図4) 。 l703 に要した時間は Gaussian 09 と Gaussian 16 で違いがみられないのに対し、l502 では 30% 程度の短縮がみられました。このことから、Gaussian 09 と比較した Gaussian 16 の時間短縮は、l502 の計算時間の短縮に起因することが確認できました。開発元に確認したところ、SCF エネルギー計算における積分を求める部分のコ ードを改修したことによる影響と考えられるそうです。

図 4　Gaussian 16 (G16) および Gaussian 09 (G09) による
l502 および l703 の計算時間 (16 並列の場合)

 

まとめ

コカインに対して Gaussian 16 の %Nproc および %CPU、Gaussian 09 を用いて力の計算を実行し、SMP 並列に用いるコア数を変えた場合の計算時間を比較しました。いずれの計算においても計算に用いるコア数を2倍にすると計算時間がおよそ 45% に短縮されました。

 

• ％NProcShared と %CPU キーワードの計算時間の比較
  Gaussian 16 において、%CPU と %Nprocshared のキーワードを用いた場合の計算時間に明らかな違いは確認できませんでした。今回は検証できていませんが、複数の異なるジョブを同時に実行した場合など、Gaussian 以外に別の仕事をするスレッドが同時に実行されていると、%CPU の利益が確認できる可能性があります。
  ※ Gaussian 16 では %CPU の利用が推奨されます。
  
  
• Gaussian 16 と Gaussian 09 の計算時間の比較
  Gaussian 09 と比較すると、Gaussian 16 は並列数によらず計算時間が 30% 程度短縮されました。これは、今回の力の計算において大部分の時間を割いていたl502 による計算時間が短縮したことに起因し、主に Gaussian 16 における SCF エネルギーを求めるための積分計算のコードの改修によるものと考えられます。