 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
非線形カーブフィッティングを使えば、独立変数と複数のパラメータからなるモデル関数を特定のデータセットに収束させることができます。この解析オブジェクトは、主として、選択したモデルがデータに可能な限りうまく当てはまるようなモデルパラメータを決定するの使用します。この場合、選択したモデルとそのパラメータに関する正確な知識が不可欠です。しかし、非線形カーブフィッティングは、特定のデータセットを補間したり平滑化する目的としても使用されます。この場合、解析のために使用するモデルの選択方法は重要ではありません。計算されたモデルパラメータについても同様なことが言えます。 この分野のアプリケーションでは、モデル同士を比較する (モデルランキング) ツールが役に立ちます。
一塊の銀に放射線を照射すると、短命の銀同位元素 47Ag108 と 47Ag110 が生成されます。これらにベータ線を再度照射します。実験では、15 秒間隔で放出されるベータ粒子を 4 分間にわたってカウントします。結果は、減少する指数曲線で、モデル関数「指数関数的減衰関数 (variant 2)」によって記述されます。パラメータ p0 はバックグラウンド放射 (background radiation) に対応し、p1 と p3 は平均寿命 p2 と p4 を持つ 2 つの励起状態の振幅に対応します。このモデルはパラメータ p2 と p4 に関して非線形であるため、非線形カーブフィッティングの手法が要求されます。
ファイル > プロジェクトデータベースを開く コマンドを選択し プロジェクトデータベースに次のパス C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Curve Fitting.fpd を指定するか、日本語フォルダ名で C:>ユーザー>パブリック>パブリックのドキュメント>Weisang>FlexPro>2021>Examples>Tutorials>Curve Fitting.fpd を指定して開きます。 Example Silver というフォルダーを開き、「Ag-Diagram」という名称の 2D ダイアグラムをダブルクリックで開きます。
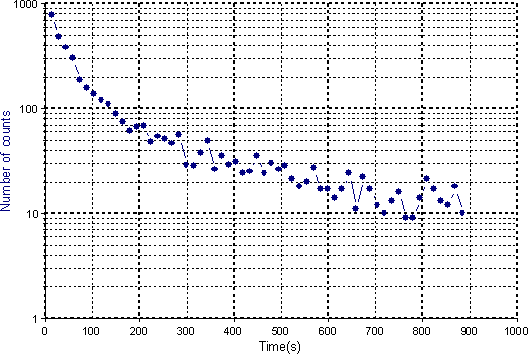
59 の浮動小数点値からなる Ag シグナルのダイアグラム (出典: Bevington, p. 142 ff)
ダイアグラムを閉じて、上記実験で解析対象となるシグナルのデータセット Ag を選択状態にします。
「挿入」タブの [解析] から 「解析ウィザード」をクリックします。
カテゴリから「カーブフィッティング」を選択し、「非線形カーブフィット」を選択します。「次へ」をクリックします。「モデルランキング」をクリックし、選択したデータセットに最も適合するモデルを決定します。
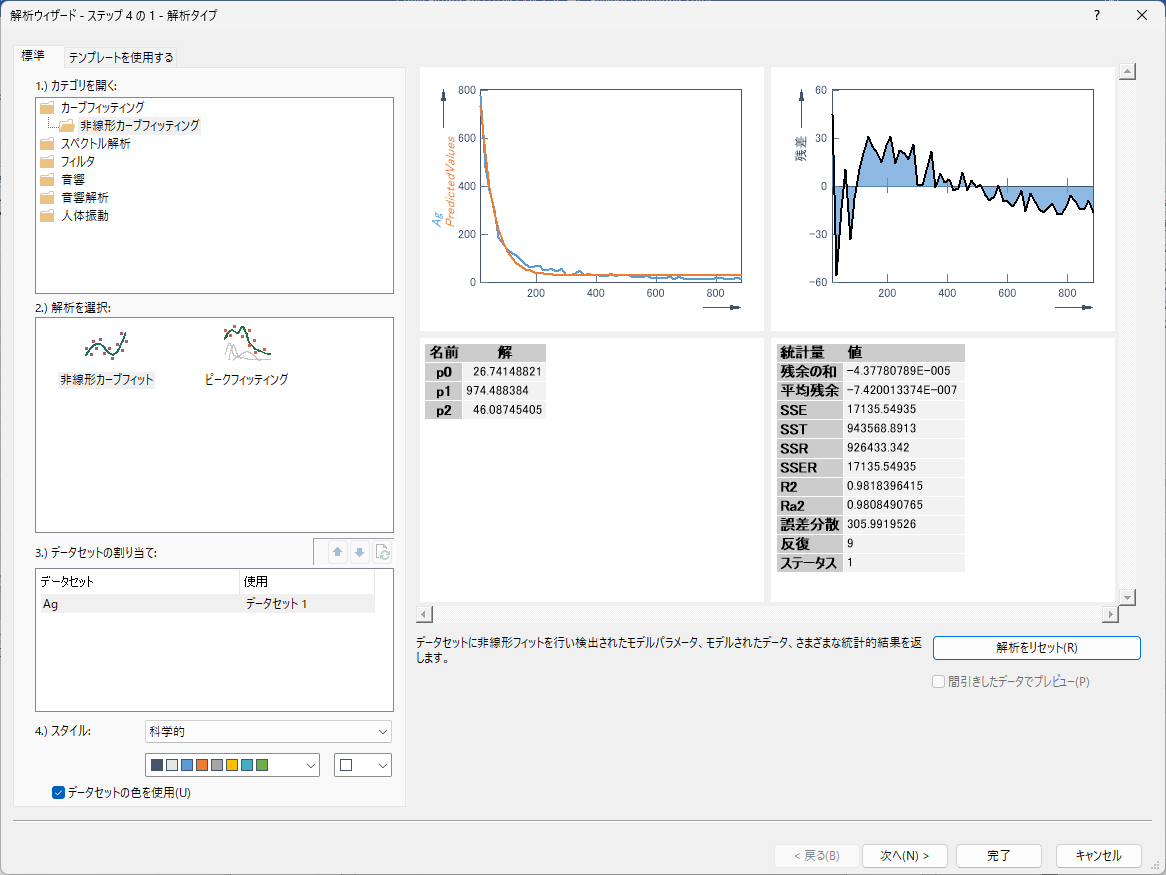
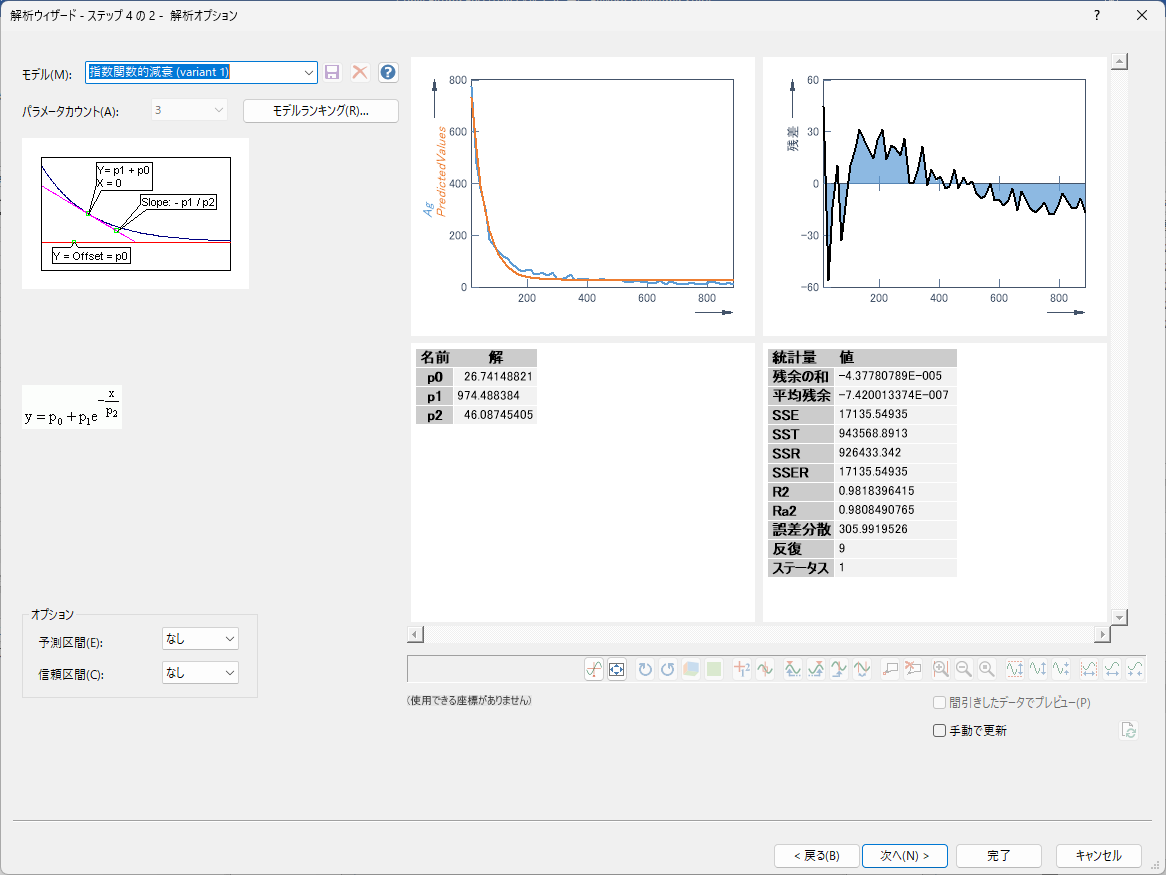
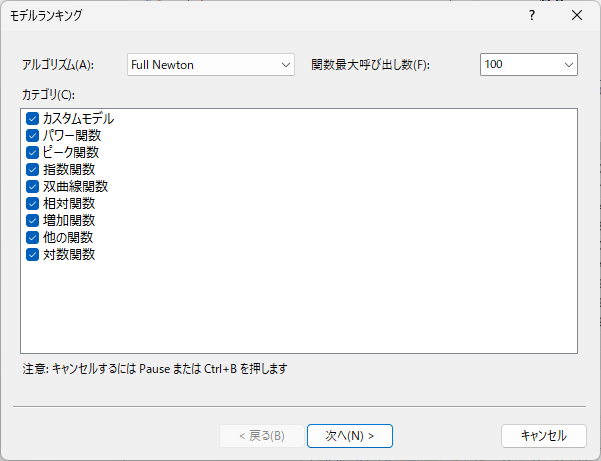
ダイアログボックスが開くと、アルゴリズム、関数最大呼び出し数、モデルのカテゴリを選択できます。個々のモデルの割り当ては「モデル」で確認できます。 「アルゴリズム」には Full Newton を設定します。関数最大呼び出し数 を 300 に設定し、すべてのカテゴリを選択します。「関数最大呼び出し数」の数を大きくすれば、それだけ多くのモデルが結果として返されますが、 それに比例してアルゴリズムの計算時間も増加します。「次へ」をクリックします。
選択したすべてのモデルでの非線形カーブフィッティングが実行され絶対残差平方和 SSE に基づいてソートされリスト化されます。このリストから引き続き使用するモデルを選択することができます。 多重決定係数 R2 もリストされます。 R2 = 1.0 は曲線がすべてのデータポイントを通過することを意味します。 X 値が分かっていればそれに相当する Y 値を正確に決定できます。 R2 = 0.0 は回帰モデルがデータの平均値を通る水平線としてしかデータを説明できないことを意味します。既知の X 値から、関連する Y 値を求めることはできません。
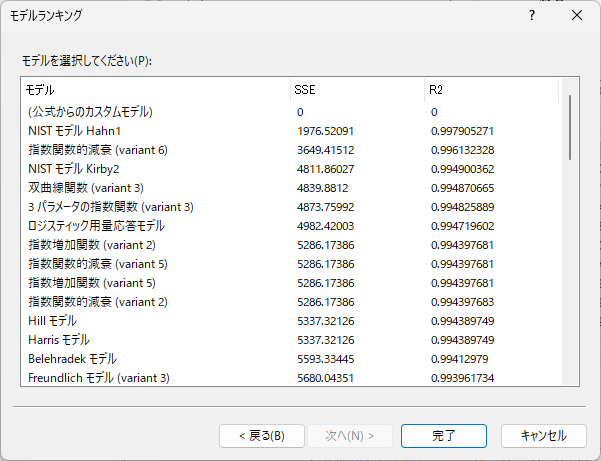
可能な限り近い収束を得るために、絶対残差平方和が最小のモデル、つまり 「NIST モデル Hahn1」モデルを選択します。次に、「完了」をクリックして「モデルランキング」ダイアログボックスを閉じます。「次へ」を2回クリックします。 「結果を表示するダイアグラムと表」 をチェックします。 次に、「終了」をクリックします。
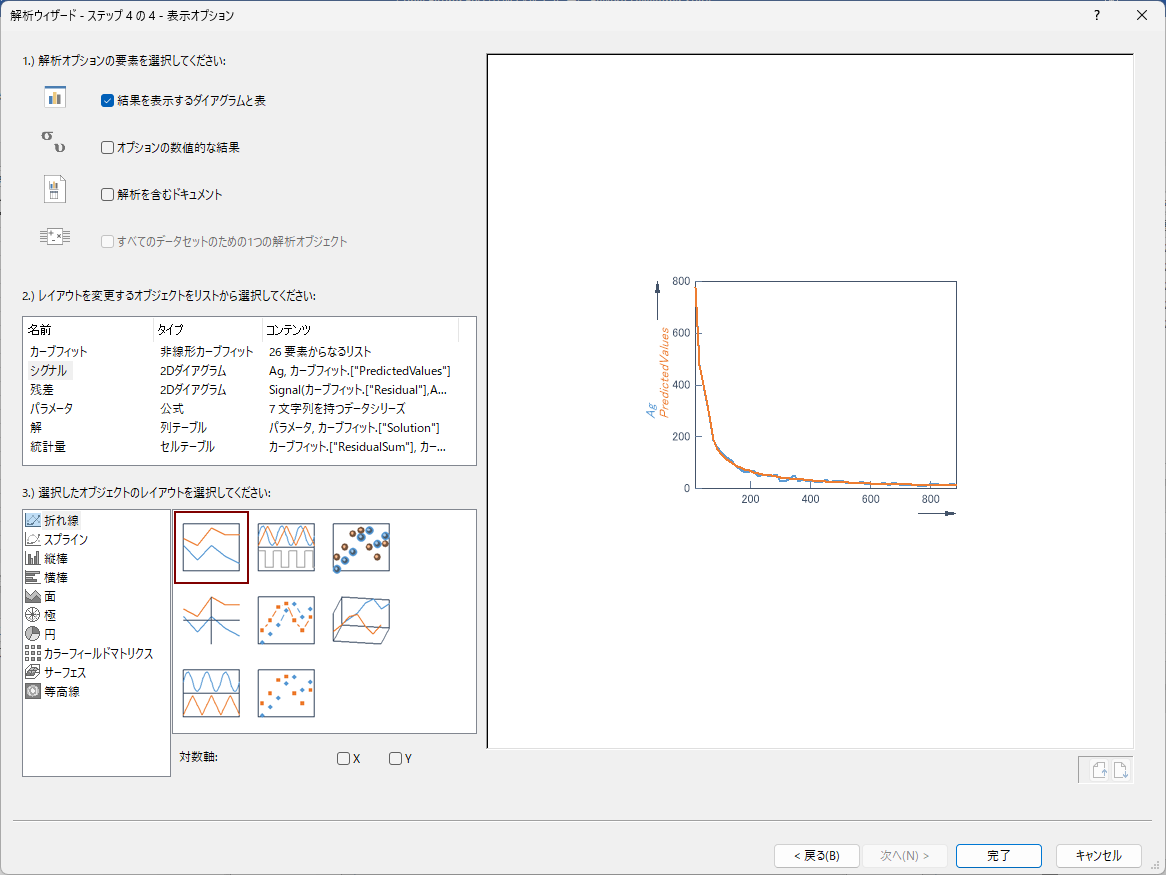
新しく作成されたダイアグラム「シグナル」を開いてシグナルのスムージング結果を確認します。次の図は、対数スケールで結果を示したものです。

非線形カーブフィッティングを使用してモデルパラメータを決定する前に、線形近似を使用してモデルパラメータを決定できるように解析対象の信号を削減し変換します。この方法は初期パラメータを求めるのに使用できます。非線形カーブフィッティングを使用してモデルパラメータの計算を成功させるには、初期パラメータの選択が、多くの場合、決定的な基準となります。このケースの線形化 (linearization) の結果は、非線形カーブフィッティングの結果の妥当性をチェックする役割を果たします。
使用するモデル関数「指数関数的減衰 (variant 2)」の式は次のとおりです。
![]()
はじめに、バックグラウンド放射 (パラメータ p0) を決定します。シグナルのカーブを見るだけで大まかな見積ができます。決定するオフセットを近似するのは指数曲線です。バックグラウンド放射の大まかな推定には最後の3つのシグナルの値を平均します。 この結果は値 13.3 です。 他のパラメータを決定するためにシグナルの各ポイントからオフセットを減算します。計算されたシグナルを二つの部分セグメント A (x < 120) および B (x > 200) に分割します。 パラメータ p3 および p4 は、対数変換と線形近似で近似します。
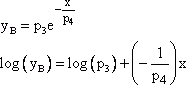
この結果に基づいて、長命成分を決定します。 次に、この部分をセグメント A から減算して、短寿命コンポーネントを決定します。
![]()
ここでは、対数変換と線形近似も行われます。 決定されたパラメータは以下の通りです:
| Parameter | Value |
|---|---|
| p0 | 13.3 |
| p1 | 808.8 |
| p2 | 37.7 |
| p3 | 135.7 |
| p4 | 187.4 |
この計算の FPScript 関数を表示するには、Example Silver フォルダーにある Linearization 数式を開きます。
パラメータの大まかな見積もりが完了したら、正確なモデルパラメータの決定を開始します。
まず、シグナル Ag を選択状態にします。
「挿入」タブの [解析] から 「解析ウィザード」をクリックします。
「カーブフィッティング」カテゴリを選択し、「非線形カーブフィッティング」を選択します。(「解析を選択」から「非線形カーブフィット」を選択します) 「次へ」 をクリックします。 指数関数的減衰 (variant 2) を選択します。 予測区間 (95%, 99% または 99.9%) と 信頼区間 (95%, 99% または 99.9%) を表示することもできます。 予測区間は反復的なデータ、すなわちそれぞれの X 値に複数の Y 値が存在する場合や、Y 値が複数の測定点の平均を示す場合に役立ちます。 95% 信頼区間は与えられた X 値において真実の Y 値が 95% の確率で存在する Y の範囲です。 予測区間は解析するデータの分散をあらわします。 収集するデータポイントが多いほど、95% のポイントは予測区間内に収まります。
モデルを選択するとウィザードのプレビューペインで非線形カーブフィッティングの結果を直接確認できます。 最初のダイアグラムには入力シグナルと推定されたシグナルが表示されます。もうひとつのダイアグラムには残差が表示されます。 両方のテーブルに推定されたパラメータと解析結果の統計量が表示されます。 モデルパラメータは以下の値となります:
| パラメータ | 値 |
| p0 | 14.0 |
| p1 | 175.4 |
| p2 | 160.4 |
| p3 | 967.2 |
| p4 | 30.1 |
このケースでは、p1 および p2 は長命成分のパラメータ、p3 および p4 は短命成分のパラメータです。
「次へ」をクリックします。ウィザードのこのページでは計算に影響を与える各種設定を行うことができます。「アルゴリズム」を選択します。 この他にも、さまざまな重み付けやスケーリングモードを設定可能です。
このページで最も重要な設定オプションは「初期値」リストです。 モデルパラメータの初期値はここで決定されます。また、パラメータが固定値を持つか否かも判断できます。 Full Newton アルゴリズムでは上方バウンドと下方バウンドも指定できます。
初期パラメータの選択は結果の計算に決定的に重要です。 選択される開始値がグローバルな最小値から遠くかけ離れていると、アルゴリズムは結果を返さないか異なる局所的な最小値を返します。 表示された結果にグローバルな最小値が存在する確率を上げるには、初期値を変えて計算してください。 4つもしくはそれ以下のパラメータのモデルでは、 「初期値の推定」オプションを使用することができます。 それぞれのパラメータで上方および下方バウンドにより決定される範囲で検出されるランダムに分布した 10 の値が計算されます。 それぞれの組み合わせにおいて絶対残差平方和が計算されます。 初期値は最小二乗平均和との組み合わせで得られます。 パラメータ初期値は FPScript の数式を使って計算することもできます。 アルゴリズムの終了基準は 関数最大呼び出し数、X 許容値、Y 許容値、F許容値、G許容値 の設定により影響を受けます。 最初の反復計算はステップバウンド設定によって変わります。
ウィザードの最後のページでは、評価する解析オブジェクトのほかにダイアグラムやテーブル、ドキュメントを作成するか指定します。 「結果を表示するダイアグラムと表」 を選択すると作成されるダイアグラムや表がプレビューペインに表示されます。 共分散行列、相関行列、パラメータの標準誤差、パラメータの信頼区間 を表示するには 「オプションの数値的な結果」を選択します。 「完了」ボタンをクリックしてウィザードを終了します。
次に、結果に局所的な最小値が存在することを明示するために、数式 Surface でモデルの「残差平方和」を計算します。 パラメータ p0 と p1 が使用可能、パラメータ p2、p3、p4 は固定です。 結果はサーフェイスダイアグラム Surface に表示されます。 最小値は p0 = 14、p1 = 176 になることに注目してください。
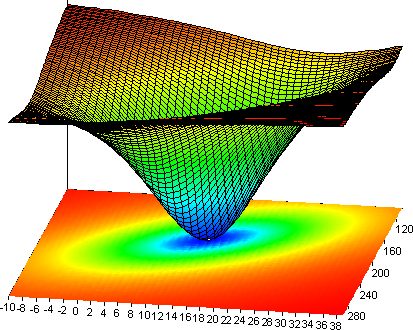
この例では、開始スクリプトを使用してモデルパラメータの初期値を計算する方法を示します。
上述の公式 Linearization を開き、公式の内容を選択 (CTRL+A) し、システムのクリップボードにコピー (CTRL+C) します。 シグナル Ag を選択状態にします。
非線形カーブフィッティングウィザードを開きウィザードの3ページ目に移動します。![]() ボタンをクリックします。入力フィールドにスクリプトコードをペースト (CTRL+V) します。 「計算」をクリックしてスクリプトをテストします。 結果は 5 つの 64 ビット浮動小数点値のデータシリーズです。「適用」ボタンをクリックして計算値を初期値として受け入れます。 計算値の数がモデルパラメータの数と異なる場合は計算値は適用できません。 スクリプトコードを入力フィールドに直接ペーストする代わりに、入力フィールドにこの数式の名称を入力することですでに作成されている数式を参照することも可能です。ただし、このコードが有効に機能するのは数式オブジェクトが存在する場合に限ります。
ボタンをクリックします。入力フィールドにスクリプトコードをペースト (CTRL+V) します。 「計算」をクリックしてスクリプトをテストします。 結果は 5 つの 64 ビット浮動小数点値のデータシリーズです。「適用」ボタンをクリックして計算値を初期値として受け入れます。 計算値の数がモデルパラメータの数と異なる場合は計算値は適用できません。 スクリプトコードを入力フィールドに直接ペーストする代わりに、入力フィールドにこの数式の名称を入力することですでに作成されている数式を参照することも可能です。ただし、このコードが有効に機能するのは数式オブジェクトが存在する場合に限ります。

定義済みのモデルに加え、独自のモデル関数を定義して、それを保存することができます。 以下の例ではカスタムモデルの作成法を説明します。 ファイル > プロジェクトデータベースを開く コマンドを選択し C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\CurveFitting.fpd でプロジェクトデータベースを開きます。 または C:>ユーザー>パブリック>パブリックのドキュメント>Weisang>FlexPro>2021\Examples\CurveFitting.fpd を指定します。Custom Model を開き、数式 Data をダブルクリックして数式を開きます。 数式は指数関数 y = p0 + p1x + p2x² + p3x³ を使用してシグナルを計算しています。 これは 1000 個の 64 ビット浮動小数点値のシグナルです。
このモデル関数は線形なので、パラメータは FPScript 関数 Approximation (数式 Linear Approximation) を使用して計算することができます。
線形カーブフィッティングを使用してパラメータを決定するには、数式 Data を選択状態にして、挿入[解析] > 解析ウィザード をクリックします。 「カーブフィッティング」カテゴリを選択し、「非線形カーブフィッティング」を選択します。 「次へ」をクリックします。「モデル」フィールドには、カスタムモデルの名称 Poly3 を入力します。モデル関数の数式またはモデル関数の偏微分の数式を入力する 2 つの入力フィールドが表示されます。数式の入力フィールドに p[0] + p[1] * x + p[2] * x^2 + p[3] * x^3 と入力します。p[0] から p[3] は特定のモデルパラメータを表します。 「パラメータカウント」リストボックスで 4 を選択します。 「保存」をクリックして指定した名前でモデルを保存します。 もし、求める結果の代わりにエラーメッセージがプレビューペインに表示される場合はウィザードの次のページで 「関数最大呼び出し数」を大きくします。 「次へ」をクリックします。 関数呼び出しを 300 に指定します。
「戻る」ボタンをクリックします。 偏導関数が数値的に計算されず、代わりに分析的に計算されることを証明するために、「導関数」テキストボックスに偏導関数を入力します: [ 1, x, x^2, x^3 ]. 偏導関数はリストとして指定する必要があります。結果として得られるモデルパラメータ推定値はさらに正確になりました。 加えて、必要な反復数は偏導関数の計算で Full Newton アルゴリズムを使用することにより顕著に減少します。「保存」をクリックしてモデルを保存します。
パラメータに名称を割り当てることもできます。これらの名称は、ウィザードの次のページにある初期値リストに表示されます。これを行うには、カスタムモデル関数を記述する数式を次のように変更する必要があります:
変数 a が変数 p[0] に割り当てられ、変数 b が変数 p[1] に、といった具合で割り当てられます。割り当ては、一行に一変数ずつ行ってください。「次へ」をクリックして、指定した名前のパラメータが 「初期値」 リストに表示されることを確認します。
「完了」をクリックしてウィザードを終了します。