 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
このチュートリアルでは、非定常データに対する FlexPro のスペクトル解析機能について説明します。この中には、短時間フーリエ変換 (STFT) と連続ウェーブレット変換 (CWT) の両方が含まれます。これらのプロシージャーは、データ ストリーム内の変化する特性を調べる場合や、従来のフーリエおよびパラメトリック解析の定常領域を識別する場合に役立ちます。
このチュートリアルでは、4つのデータ領域のそれぞれに異なる周波数の正弦波が含まれる非定常データセットを使用します。
ファイル > 開く > 参照から下記のパスにあるプロジェクトデータベースを開きます。
または、日本語のフォルダ名で C: > ユーザー > パブリック > パブリックのドキュメント > Weisang > FlexPro > 2021>Examples>Tutorials>Spectral Analysis.fpd に移動します。Tutorials フォルダを開いたら、Time-Frequency Analysis サブフォルダを開いて、Data という名称の 2Dダイアグラムをダブルクリックして開きます。
このシグナルのグラフは以下のとおりです。浮動小数点値が 1024 個あります。
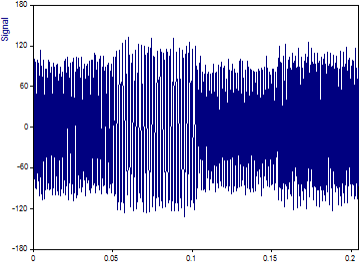
X (時間) 値は 0 から 0.2047 まで変化し、サンプルの増分は 0.0002 です。したがって、ナイキスト周波数は 2500 (サンプリング レート 5000 の半分) です。4 つの正弦波は、以下に示す振幅、周波数、位相で生成されました。
10% のランダムガウス (ホワイト) ノイズを追加して、-20 dB のノイズ フロアを作成します。
まず、このデータセットの基本的なフーリエスペクトルを調べます。
ダイアグラムを閉じて、データセット Signal を選択状態にします。
挿入 [解析] > 解析ウィザードをクリックします。
「スペクトル解析」の「フーリエ解析」を選択します。「フーリエスペクトル」アイコンをクリックします。「次へ」をクリックします。
スペクトル タイプには「振幅」を選択します。ウィンドウ タイプには、「矩形 -13dB W=1 」を選択します。FFT 長がデータ長または 1024 に設定されていることを確認します。オプションで最大ピークカウントを選択し、値 4 を入力します。次に、ホワイト ノイズの許容限界 % を「なし」に設定します。ピークの上にラベルが表示されていない場合は、振幅ラベルが表示されるまで「ラベルの切り替え」をクリックします。
解析ウィザードのフーリエ プロットは次のようになります:
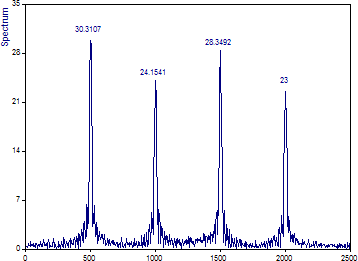
フーリエスペクトルでは4つの連続する成分の周波数が正しく識別されますが、これらの高調波が時間的にどこで始まりどこで終わるかは示されません。各成分の持続時間は無限であると想定されるため、時間軸上の局在性に関する情報はすべて失われます。
さらに、各成分は全データ長の約 4 分の 1 だけ存在するため、各振幅は過渡高調波の値の約 4 分の 1 になります。
フーリエスペクトルを正確にするためには、シグナルは広い意味で定常である必要があります。つまり、サンプリング期間全体にわたって、スペクトルの中身は周波数とパワーの両方で一定にする必要があります。CWT と STFT 解析はどちらも、データの時間と周波数のスペクトルを提供するため、非定常信号の解析に効果的です。
短時間フーリエ変換 (STFT) は、各セグメントの中央に時間値が割り当てられていることを除いて、ピリオドグラムやセグメントオーバーラップ FFT に似ています。スペクトルピークから振幅やパワーを直接取得する必要がない限り、通常はデータテーパリングウィンドウを使用して、可能な限り最適な時間軸上の局在性を特定します。
時間周波数スペクトルは本質的に曖昧です。時間の解像度が高くなるほど、周波数の解像度は低くなります。STFT は、この効果をよく理解するための最良の方法です。
「戻る」をクリックして、解析ウィザードのステップ 1 に戻ります。「時間周波数解析」を選択し、そこから「STFT」を選択します。「次へ」をクリックしてステップ 2 に進みます。スペクトルプロシージャーに「短時間フーリエ変換 (STFT)」 が自動的に選択されます。
「スペクトルタイプ」には、「正規化 dB」を選択します。ウィンドウの「タイプ」を「Cos2 ハミング -31dB W=2」に設定します。最初は既定値が選択されています。FFT 長が「セグメント長」に設定され、「セグメント長」が 256 (データ長の 1/4 に相当) になっていることを確認します。「% の重なり」を 50 に設定します。
通常、時間周波数スペクトルで行われるように、時間を X 軸に沿って配置するには、「周波数が Z、時間が X」をオンにします。最大 dB 範囲を 20 に設定し、最大 STFT 周波数値を「無制限」のままにします。
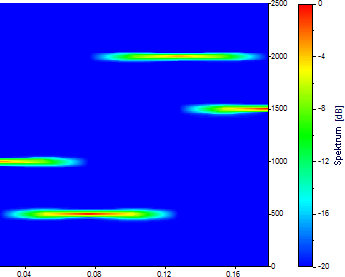
これらの設定により、それぞれの長さが 0.05 秒の7つの時間スナップショットが生成されます。周波数は 129 個あります。周波数 500、1000、1500、2000 の成分は明確に定義されていますが、時間の定義が非常に不十分なため、4つの高調波の連続性は不明瞭になっています。また、スナップショットに割り当てられる時間はそのセグメント内の平均時間であるため、2つの時間境界にスペクトル情報が利用できない領域がかなりあります。
時間的に密度を高める非常に簡単な方法は、「% の重なり」を増やすことです。
「% の重なり」を 90 に変更します。
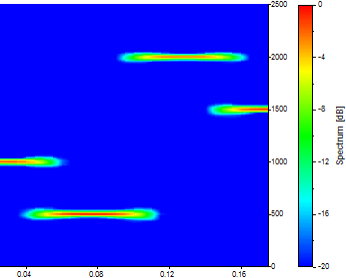
これにより、このスペクトルを構成する時間スナップショットは 31 個になります。周波数は同じく 129 個存在します。これにより時間分解能が若干向上しますが、各スナップショットは依然としてデータの 4 分の 1 の平均です。時間分解能を向上させるには、セグメント長を短くする必要があります。
セグメント長を半分にするには、128 に変更します。「% の重なり」は 90 のままにします。
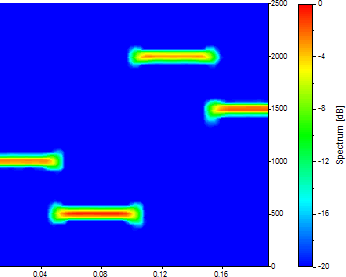
現在、時間セグメントは 75 あり、それぞれはデータの 8 分の 1 の平均になります。周波数は 65 です。時間と周波数のトレードオフが明らかになりました。時間の定義ははるかに明確になりましたが、周波数の解像度は大幅に低下しました。
セグメント長を 64 に変更します。「% の重なり」は 90 のままにします。
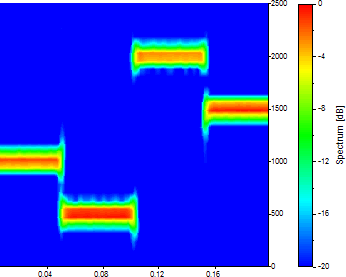
時間セグメントは現在 161 となり、それぞれはデータの 1/16 の平均です。周波数は 33 です。時間の定義はさらに改善されましたが、周波数の解像度は大幅にあいまいになっています。これをさらに進めます。セグメント長を 32 に変更します。「% の重なり」は 90 のままにします。

時間値は 331 になりましたが、スペクトルグリッドには周波数ノードが 17 しかありません。時間スナップショットはデータの 1/32 にわたる平均をあらわしているため、時間の定義は非常に明確です。一方、周波数領域ではピークがほぼ一致しています。
3D サーフェス プロットを使って、可視化をより明確にする方法もあります。
「標準ビュー」をクリックします(「次へ」をクリックしてステップ3の3でオブジェクトのレイアウトに「サーフェス」を選択します)。3D レンダリンググリッドを改善するには、FFT 長を 128 に変更します。
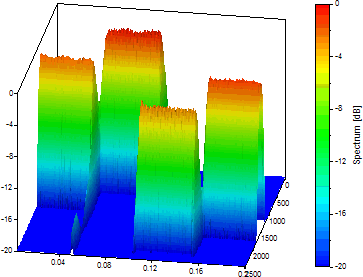
これは、時間の解像度を優先したときの時間と周波数のトレードオフを可視化するのに適した方法です。ここで、周波数を優先する初期設定に戻ります。
セグメント長を 256 に設定します。FFT 長を「セグメント長」に設定し、「% の重なり」を 90 に設定します。
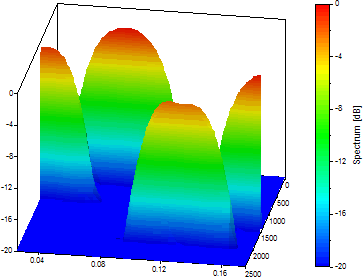
これは、時間の大幅な曖昧さを犠牲にして周波数の解像度を優先したときの時間と周波数のトレードオフを視覚化した優れた例です。
STFT の各種パラメータを最適化することは容易ではありません。STFT 手法では分解能は固定です。スペクトル中には、周波数に関係なくの時間と周波数と同様のトレードオフがどこにでもあります。STFT では注意深い微調整が必要ですが、スペクトルピークの高さからその振幅とパワーを容易に得ることができます。テーパリングウィンドウを使用して振幅に正規化を設定するか、または、矩形ウィンドウで「% の重なり」に高い値を組み合わせて使用します。
スペクトル タイプを「振幅」、ウィンドウのタイプを「矩形 -13dB W=1」 (ウィンドウなし)、セグメント長を 64、FFT 長を 256、「%の重なり」を 90 に設定すると、次のグラフが表示されます。
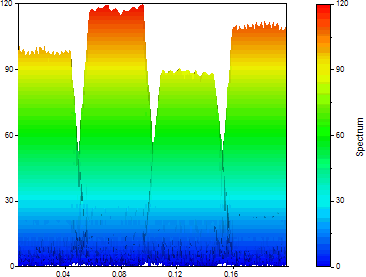
STFT では位相をシフトした複数の正弦関数を基底関数に使用します。正弦関数の持続時間が無限であれば、データストリームを複数のウィンドウセグメントに分ける変換をおこなう必要があります。もし、基底関数自体の持続時間が有限であれば、これらを持続時間が有限のマザーウェーブレットとしてシフトおよび拡大・縮小させ、これとデータストリームとの相関関係からスペクトルを決定できます。
これが連続ウェーブレット変換 (CWT) の本質です。
ウェーブレットの形状は多種多様ですが、ウェーブレットを時間周波数スペクトル解析使用する方が、STFT を最適化するよりも一般的に簡単です。また、多くの場合、マザーウェーブレットの種類と設定の違いは、時間周波数スペクトルの結果に大きな影響を与えません。一般にマザーウェーブレットと調整可能なパラメータの選択は、時間周波数のトレードオフの選択に関連します。
「連続ウェーブレット変換 (CWT)」を選択し、スペクトルタイプに「正規化 db」を選択します。ウェーブレットのタイプを 「Morlet」 に設定し、「調整」 (波数) を 8 に設定します。「畳み込みゼロパッド」を 1024 (1024 データを 2 の次の累乗である 2048 にパッド) に設定し、「周波数の数」を 40 に設定し、開始周波数を 0、終了周波数を 2500 (完全なナイキスト範囲) のままにします。「周波数が Z」にチェックされていること、「最大 dB 範囲」が 20 に設定されていること、「最大 CWT 時間値」が 1024 (1024 データ長に完全に対応するため) であることを確認します。
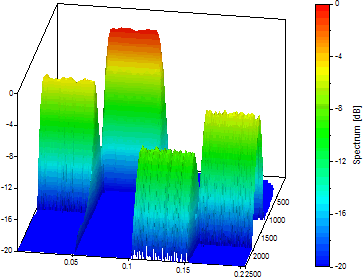
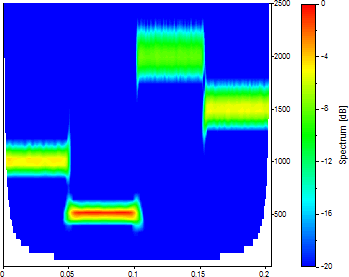
これは、優れた CWT 時間周波数スペクトルです。実際、マザーウェーブレットやその調整可能なパラメータの値に関係なく優れた結果が得られます。時間周波数解析のすべての作業に、波数 8 の Morlet ウェーブレットを使用すれば、データの振動と形状が最も適合し、その振動数が最適な時間周波数解像度になるウェーブレットを選択することで得られる最適化を見逃すことはありません。
この事実を確認するために、FlexPro で提供される極端な例を調べてみましょう。
ウェーブレット解析における時間と周波数のトレードオフを評価するために、等高線図を復元します。「平面図」をクリックします。
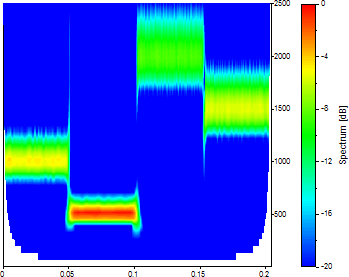
「調整」の波数を 20 に変更します。
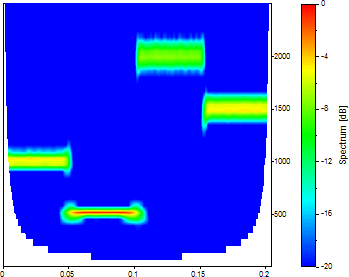
Morlet で調整可能なパラメータ (波数) を 20 にすると、周波数軸上の局在性は向上しますが、時間軸上の局在性は低下します。
「調整」を 50 に変更します。
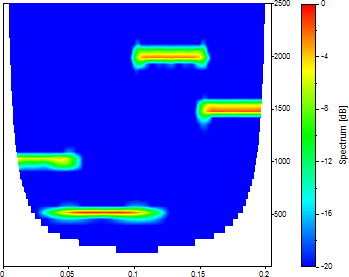
Morlet で調整可能なパラメータ (波数) を 50 にすると、周波数は明確に定義されますが、時間軸上の局在性は低下します。
ウェーブレットのタイプを「Gaussian Derivative」に設定し、調整を 2 に設定します。
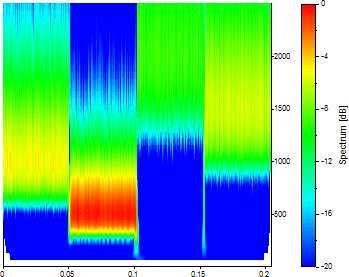
Gaussian Derivative ウェーブレットで調整可能なパラメータを 2 にすると、時間軸上の局在性は最も鮮明になりますが、周波数軸上の局在性は明らかに非常に曖昧になります。
CWT は、多重解像度の時間周波数手法です。前に作成したプロットをよく見ると、周波数の最も低いピークにスペクトルが最大の CWT があり、全4つのシグナル成分中でスミア (にじみ) の度合いが最も低いことがわかります。周波数が最も高いピークは、一貫してスペクトルが最低の大きさを示し、4つの成分の周波数のうち最もスミア (にじみ) の度合いが高くなっています。
この特性は、設計上の考慮事項ではなく、CWT アルゴリズムの副産物です。多重解像度解析には利点と欠点があります。もし、高周波成分が非常に短い時間で断続的である場合は、時間軸上の出現と消失を正確に捉えるために周波数軸の解像度をトレードオフすることが最適な選択となります。もし、低周波成分が長時間持続する場合は、より正確な周波数推定のために時間軸の解像度をトレードオフすることが最適な選択となります。CWT の多重解像度解析が有利になるのはこれらの条件が満たされていることです。
もし、持続性が周波数に依存しない場合や、スペクトルの大きさから振幅とパワーを直接取得することが主要目的である場合、CWT の多重解像度プロパティは欠点となります。
従来のウェーブレット解析に使用されてきた離散ウェーブレット変換 (DWT) とは異なり、連続ウェーブレット変換 (CWT) は任意の周波数セットで評価できます。これらの周波数は冗長性の任意の尺度で重複可能で、線形、対数、または、任意のシーケンスで間隔を空けることができます。評価する周波数ごとに個別の FFT を保存する必要があるため、FlexPro では周波数の総数が 500 に制限されています。この周波数の冗長性により、 CWT は DWT と比べてはるかに高い解像度を提供できます。
ウェーブレットのタイプに Morlet を選択し、波数を 12 に設定します。周波数の数として 100、開始周波数として 400、終了周波数として 1200 を指定します。
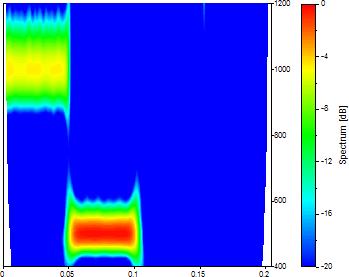
これにより 400 ~ 1200 の周波数帯域に CWT スペクトル解析の完全な解析能力が集中しています。
CWT で使用する FFT は、変換によってスペクトルを生成する従来のフーリエ解析とは異なり、スケーリングと変換を行ったウェーブレットとデータストリームとの高速畳み込みを実行する目的に限り使用されます。CWT の基底関数は、スケーリングとシフトを行うウェーブレットであり、フーリエ解析の正弦関数や余弦関数ではありません。CWT でゼロパディングをおこなう唯一の目的は、高速畳み込みプロシージャーにおいてラップアラウンド効果 (エイリアシング) を回避することです。FFT 長がデータストリームの長さの 2 倍の場合、すべての周波数でラップアラウンドは完全に回避されます。多くの場合、次にくる 2 のべき乗までゼロパディングすれば、知覚できるラップアラウンドを回避すると同時に、可能な限り高速な畳み込みを実現できます。
高速畳み込みに exact-N FFT を使用すると、低周波数におけるラップアラウンドがすぐに明らかになります。このラップアラウンド効果は周波数とともに減少します。これが、最高周波数成分でラップアラウンド効果がない理由です。低周波数成分が無視できるほど小さい場合、または処理される帯域内でデータが周期的である場合は、ゼロパディングを使用する必要はありません。
この影響を避けるためにゼロパディングを使用すると、ラップアラウンドに関連するパワーが破棄されます。その結果、データレコードの端付近のパワーが減少します。パワーが減少する可能性のあるこのゾーンを CWT 用語では円錐状影響圏と言います。円錐状影響圏は、周波数間隔が対数である場合に特に重要です。
Morlet の波数を 100、ゼロパッドを 0、周波数の数を 40、開始周波数を 0、終了周波数を 2500 に設定します。
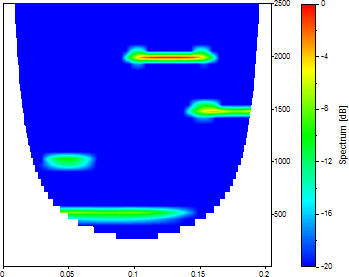
この場合、波数が非常に大きいため、円錐状影響圏ははるかに大きくなります。最低周波数成分は実際には時間スケールの右側に回り込みます。この円錐状影響圏の情報はプロットされないため、FlexPro では表示されません。
Morlet の波数を 12 に設定し、「次へ」をクリックします。ステップ 3 の両方のオプションをオンにし、「完了」をクリックします。
合計4つのオブジェクトが FlexPro プロジェクト データベースに作成されます。
「スペクトル」は解析オブジェクトです。これはスペクトル解析を実行するオブジェクトです。解析オブジェクトはダブルクリックすると開くことができます。
「スペクトル」は、解析ウィザードによって生成された時間周波数スペクトルプロットです。スペクトルオブジェクトが使用されています。
「データ」は、オリジナルの時間領域データのプロットです。
「時間 - 周波数」は、スペクトルとデータのプロットを内容とするドキュメントです。
デジタルシグナル処理に関する優れた入門書:
FlexPro で使用される FFT アルゴリズムについて:
データテーパリングウィンドウに関する情報:
ウェーブレット解析を現実世界のデータに適用する際の微妙な点を理解したい人のために、CWT を徹底的かつ分かりやすく解説した論文:
この参考文献では、エルニーニョ時系列データの解析という観点から CWT について説明しています。著者らは、FORTRAN パブリック ドメイン CWT ウェーブレット解析パッケージ WAVEPACK も公開しています。ドキュメントと WAVEPACK コードは、下記から入手できます。http://paos.colorado.edu/research/wavelets/