 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
このチュートリアルでは、自己回帰パラメトリックモデリングと固有値解析プロシージャに関連する FlexPro のスペクトル解析機能について説明します。これらの高度な手順は、特にデータレコードが非常に短い場合の周波数推定に重要となります。
AR および ARMA スペクトル推定器は、自己回帰 (AR) または自己回帰移動平均 (ARMA) モデルを使用して時間領域データのスペクトルを推定するモデリングプロシージャーです。固有値解析ではノイズ固有モードを使用して、狭帯域のシグナル成分のみを含む直交周波数スペクトルを再構築します。これら 3 つのアルゴリズムはいずれも周波数推定器と言えます。つまり、これらのプロシージャーは、存在する高調波の周波数を非常に高い精度で推定できます。ただし、これらの手順では一般に、各成分のパワーについては、正確に測定することはできません。
これらの手法は計算量が多いため、フーリエ解析では十分な解像度が得られない小規模なデータ セットに最も役立ちます。また、シグナルデータは定常であることが想定されるため、シグナルがほぼ定常である (全体的なスペクトル内容が変化しない) と想定できるデータストリームの小さなセグメントを抽出することに役立つ場合があります。このチュートリアルでは、データ長が短いテストサンプルを使用しますが、これよりはるかに大きなデータセットの一部を使用することも可能です。
このチュートリアルでは、データ長 64 の短いシグナルを使用します。この内容は、フーリエ解析では分解できないほど狭い周波数間隔をもつ3つの正弦波です。
Dim x x = Series(0, 0.0126, 0.0002) Signal(100*Sin(2*PI*x*420+PI/2)+50*Sin(2*PI*x*500+PI)+100*Sin(2*PI*x*580+3*PI/2), x)
サンプリングレートは 5000 Hz で、ナイキスト周波数は 2500 Hz で、検出可能な最大周波数です。この周波数を超える振動情報は、より低い周波数にエイリアシングされます。時間値は、サンプルの増分 0.0002 で 0 から 0.0126 まで変化します。10% のランダムガウスノイズを追加します。これにより、最大ピークに対して約 -30 dB のノイズ フロアが生成されます。
中央の正弦波は、他の2つの正弦波の半分の振幅、つまり 4 分の 1 のパワーになります。これは高ダイナミック レンジのテストではなく、3つのピークすべてが大きなパワーを持つデータセットである点に注意してください。この中央のピークは、他の 2 つのピークより -6 dB しか低くありません。そのため、フーリエ領域で最適化しても、この 4 分の 1 のパワー を持つ中央のピークの分解にはほとんど影響しません。
ファイル > 開く > 参照から下記のパスにあるプロジェクトデータベースを開きます。
または、日本語のフォルダ名で C: > ユーザー > パブリック > パブリックのドキュメント > Weisang > FlexPro > 2021>Examples>Tutorials>Spectral Analysis.fpd に移動します。Tutorials フォルダを開いたら、Frequency Estimators サブフォルダを開いて、Data という名称の 2Dダイアグラムをダブルクリックして開きます。
このシグナルのグラフは以下のとおりです。浮動小数点値が 64 個あります。

ハミングデータテーパーを使用して、片側フーリエ幅 2 の最大サイドローブ減衰を実現します。
グラフウィンドウを閉じて Signal データセットを選択状態にします。
挿入 [解析] > 解析ウィザードをクリックします。
「スペクトル解析」の「フーリエ解析」を選択します。「フーリエスペクトル」アイコンをクリックします。「次へ」をクリックします。
「スペクトルプロシージャ」で「フーリエスペクトル」がチェックされていることを確認してください。解析ウィザードのステップ1で、どの スペクトルプロシージャ が選択されていてもステップ2で修正できます。
「スペクトルタイプ」 には「正規化 dB」を指定します。
これにより、スペクトルの最大ピークが 0 dB に正規化されます。他のすべてのピークは負の値になります。-3 dB のピークは 0 dB ピークの半分のパワーになり、-6 dB のピークは振幅が半分になり、この値が3つのピークの中の中央になることが予想されます。?
ウィンドウタイプに「Cos2 ハミング -43dB W=2」を選択します。
FlexPro のスペクトル解析モジュールでは、すべての固定幅 (調整不可) データ テーパーが、名前、サイドローブ減衰 (dB)、片側フーリエ領域のピーク幅で一覧表示されます。このうち、矩形ウィンドウは、すべてのデータ要素が 1 倍されるため、ウィンドウ処理なしと同じです。

「FFT 長」が「データ長」または 64 に設定されていることを確認します。
「ゼロパッド」情報フィールドには、ゼロパディングが行われなかったことが示されます。
「最大ピークカウント」オプションを選択し、値 3 を入力します。
解析ウィザードには、スペクトル ピーク情報が自動的に生成されます。このオプションを 3 に設定すると、パワーの大きさが上位 3 つのピークが出力されます。最大ピークから下の dB しきい値を設定することもできます。このデータ セットでは、最大ピーク 0 から 65 dB 下のしきい値を簡単に設定できます。
ここで、「ホワイトノイズの許容制限 %」 を「なし」に設定します。
ピークの上にラベルが表示されない場合は、周波数ラベルが表示されるまで「ラベルの切り替え」をクリックします。
「ラベルの切り替え」では、複数の設定のいずれかを選択できます。ラベルの状態を切り替えて、スペクトルの y 成分 (ここでは正規化された dB)、x 成分 (常に周波数)、または、ピーク情報「なし」を表示できます。
解析ウィザードのフーリエ プロットは次のようになります。
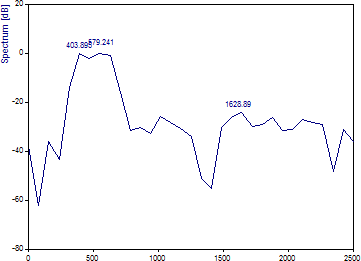
FFT 長を 8192 に設定します。
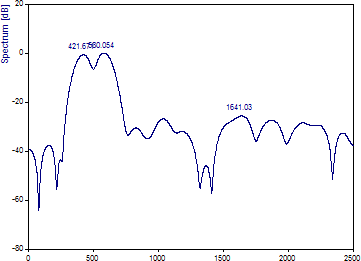
ゼロパディングによって導入された補間により、420 と 580 の最高パワーのピークはより正確に分解されますが、サンプル長が短すぎて、周波数 500 の低振幅正弦波の分解は出力されません。この特定のデータ サンプルのフーリエ解析に必要な解像度をもたらす方法はありません。必要なのは、より長時間サンプリングすることです。この同じデータ ストリームを 2 倍の長さでサンプリングするとどうなるかを見てみましょう。
「キャンセル」をクリックします。 データセット Signal2 を選択状態にします。
もう一度、解析ウィザードを選択します。スペクトル解析の下にある「フーリエ解析」カテゴリを選択します。次に、「フーリエ スペクトル」を選択します。「次へ」をクリックします。スペクトル タイプを「正規化 dB」に、ウィンドウ タイプを「ハミング -43dB W=2」に設定します。FFT の長さを 8192、最大ピークカウントを 3、ホワイト ノイズの許容限界 % を「なし」に設定します。ピークの上にラベルが表示されていない場合は、周波数ラベルが表示されるまで「ラベルの切り替え」をクリックします。
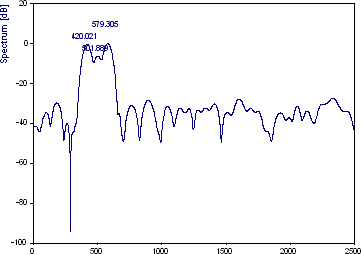
420 Hz 成分は 420.02 として、500 Hz 成分は 501.89 として、580 Hz 成分は 579.30 として検出されます。3 番目のピークはパワーが最大であるため、0 dB です。最初のピークは -0.21 dB、中央のピークは -6.20 dB でした。
このサンプル長では、3 つの成分を分解するのに十分なフーリエ分解能があります。分解能の境界線上にあるにもかかわらず、周波数とパワーの推定値の精度が非常に優れている点に注意してください。この演習の目的は、代替手順に移る前にフーリエ手法を徹底的に調査することのメリットを示すことです。
しかし、より長い時間サンプリングしてもデータの情報量を増やすことができない場合はどうなるでしょうか。データが急速に変化するシグナルから取得されたほぼ静止したスナップショットである場合は、より長いサンプルを使用しても周波数分解能を高めることができない可能性があります。このような場合には、パラメトリック AR および ARMA と固有値解析プロシージャーが必要です。
ここで紹介する周波数推定法は、データ長が短すぎて十分なフーリエ解析の解像度が得られない場合に有効な方法です。
「キャンセル」をクリックします。最初に使用したデータセット Signal を選択状態にします。これには 64 個のデータ要素が含まれます。
もう一度、解析ウィザードを選択します。スペクトル解析の下にあるスペクトル推定カテゴリを選択します。次に、「AR スペクトル推定」を選択します。「次へ」をクリックします。
アルゴリズムに「データマトリクス FB SVD」を選択します。
シグナルとノイズの本質的な分離は、自己相関、Burg、正規方程式 FB、データマトリックス FB の各プロシージャーでは行われません。これらのプロシージャーは歴史的に AR 解析に使用されてきたものであることから、比較分析を目的として FlexPro に用意されているものです。これらのプロシージャーでは、スペクトル分析において危険な偽ピーク、分割ピーク、その他の異常が発生する可能性があります。推奨されるのは、「正規方程式 FB SVD」、および、「データ マトリックス FB SVD」 プロシージャーのみです。
処理時間がとても長い場合は、「正規方程式 FB SVD」プロシージャーが必要になることがあります。これは、非常に長いデータ セットの場合、「データ マトリックス FB SVD 」プロシージャーよりもはるかに高速です。
「スペクトルタイプ」を 「dB」 に設定します。「次数」を 40 に、「シグナルサブスペース」を 6 に設定します。
次数が 40 の場合、係数が 40 個の AR モデルが生成されます。シグナルスペースが 6 の場合、6 つの固有モードのみがシグナルとして扱われます。その他の 34 個の固有モードはノイズとして扱われ、AR 係数の SVD 計算では破棄されます。シグナルとノイズの本質的な分離により、スペクトルに対するノイズの影響が除外されます。
なお、スペクトル成分を追加するごとにシグナルのサブスペースを 2 増やす必要がある点に注意してください。たとえば、3 つのスペクトル成分をマッピングするには、シグナルサブスペースを 2 倍の 6 に設定する必要があります。また、これらの手順では、スペクトル内のピークにラベルを付ける際に、ピークの最大数を指定する必要がないことにも注意してください。非 SVD アルゴリズムの場合、ピーク数は AR 多項式の根によって決定され、SVD プロシージャーの場合はシグナルスペースによって決定されるためです。
「適応スペーシング」オプションにチェックを入れます。
「適応スペーシング」オプションでは、適応型の周波数の全範囲のスペクトルが提供されます。ピークが鋭く、スペクトルの大きさが急速に変化する領域ではポイントが多く取得され、また、スペクトルの振幅がゆっくりと変化する領域ではポイントは少なく取得されます。
ピークの上にラベルが表示されない場合は、周波数ラベルが表示されるまで「ラベルの切り替え」をクリックします。
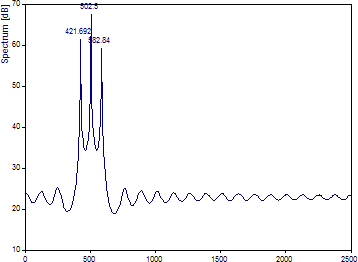
フーリエ解析では中間周波数の高調波を分解することはできませんが、適切に設計された AR スペクトル解析では3つのスペクトル成分が明確に復元されます。非常に鋭いスペクトル ピークは、AR スペクトルの高調波に典型的に見られるものです。
420 Hz 成分は 421.69 として、500 Hz 成分は 502.5 として、580 Hz 成分は 582.84 として推定されます。これと同じ 64 ポイントサンプルのフーリエスペクトルと比べるとかなり印象的ですが、フーリエ解析では長さ128 サンプルではより正確な周波数推定値が生成されていることに注意してください。また、AR ピークの振幅は、パワープロファイルや振幅プロファイルの逆であることにも注意してください。スペクトル内で最も振幅が大きいのは中央の成分であることが示されています。これが、AR 法が主に周波数推定のみに用いられるべき理由です。ここでも、成分の振幅とパワーを推定するには、高調波解析オプションの 2 段階のプロシージャーを使用する必要があります。
ここで、アルゴリズムに「データマトリクス FB」 を選択します。
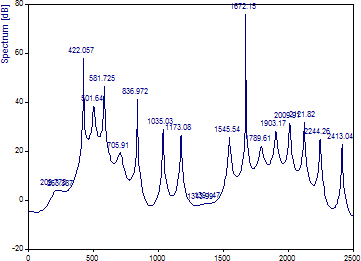
これは、従来の AR スペクトル解析が歴史的にどのような結果を生み出してきたか、そして、なぜ多くの分野で評判が悪かったのかを示す理由です。AR 係数の計算に本質的なシグナルとノイズの分離がない限り、AR モデルは通常、モデル オーダーの半分のピークを生成し、これらの一部が偽であることは珍しくありません。ターゲットとする3つの ピークよりも大きいスペクトル 振幅がノイズ ピークにあることが示されています。
アルゴリズムに「自己相関」法を選択します。
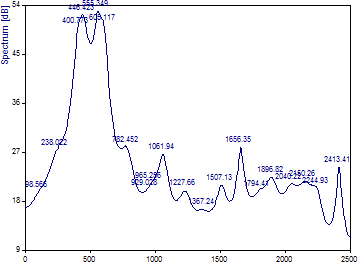
このプロシージャーによる AR フィルターは、常に安定しているため (AR 多項式の複素根は常に単位円の内側または上にある)、他の非 SVD アルゴリズムで発生しやすい誤ったピークは発生しにくくなりますが、この方法では周波数分解能が大幅に劣ります。この AR 方法では中央の成分を分解できていない点に注目してください。
固有解析法は、最も正確な周波数推定法である一般的に考えられています。MUSIC (MUltiple SIgnal Classification) アルゴリズムと固有ベクトル アルゴリズムは、シグナル内の狭帯域成分を正確に推定するために広く使用されています。
スペクトルプロシージャに「固有値 (MUSIC、EV) 」を選択し、アルゴリズムに「MUSIC」を選択します。スペクトル タイプに「 dB」、次数に 40、シグナルサブスペースに 6 が設定されていることを確認します。「適応スペーシング」オプションはそのままにします。
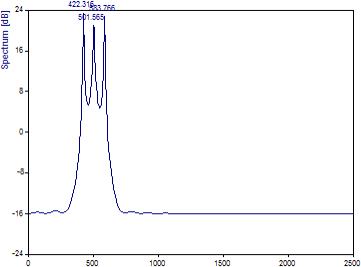
420 Hz 成分は 422.32、500 Hz 成分は 501.56、580 Hz 成分は 583.77 として推定されます。ここでも、同じ 64 ポイント サンプルのフーリエ スペクトルと比べると印象的ですが、フーリエ解析の長さ128 のサンプルではより正確な周波数推定値が生成されます。
さらに、これらの推定値は AR プロシージャほど正確ではありません。ただし、ここでは、スペクトルの中央の成分の振幅が小さいことが示されています。この例では正しいプロファイルですが、固有解析法も同様に周波数推定値としてのみ考慮されます。成分の振幅とパワーを推定するには、やはり、高調波解析オプションの 2 段階のプロシージャーを使用する必要があります。
「EV (固有ベクトル)」アルゴリズムを選択します。」
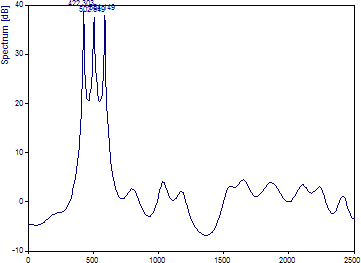
420 Hz 成分は 422.30、500 Hz 成分は 502.55、580 Hz 成分は 584.14 として推定されます。このデータの場合、隠れた周波数を回復するのに、MUSIC プロシージャーがわずかに効果的でした。
これらのプロシージャーでは、シグナルスペクトルがノイズ固有モードを使用して生成されるため、このシグナル内のノイズを十分にマッピングするには、常に多数のノイズ固有モードが必要です。MUSIC アルゴリズムと EV アルゴリズムの違いは、異なるノイズ固有モードの重み付け方法のみです。
ここでは、スペクトル成分の振幅とパワーを2段階の高調波解析を使用して抽出します。
「戻る」をクリックします。「高調波解析」を選択し、「高調波推定」を選択します。「次へ」をクリックします。
アルゴリズムに「AR データマトリクス FB SVD」を選択し、成分の数に「最大カウントによる」を選択します。最大カウントに 3 を設定し、結果のタイプに「高調波成分」を設定します。次数を 32 に設定します。
この2段階プロシージャーでは、次数により低い値を指定する必要があります。モデル次数がデータ長の 1/2 を超えると、異常が発生する可能性があります。この自動化された 2 段階のアルゴリズムでは容易に確認できないこれらの影響を防ぐために、FlexPro は高調波スペクトルのモデル次数をデータ長の 1/2 に制限します。
「ラベルの切り替え」をクリックして、振幅ラベルを表示します。
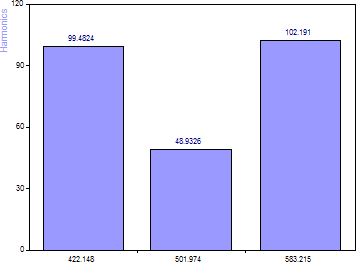
[100, 50, 100] の振幅が数パーセント以内に回復されていることに注意してください。
「次へ」をクリックします。ステップ 3 ですべてのオブジェクトを選択します。「完了」をクリックします。
FlexPro のオブジェクトリストにある高調波推定 (列テーブル) をダブルクリックします。

オリジナルのシグナルで使用した位相は、π/2、π、3π/2 でした。通常、最小の誤差は周波数で発生し、最大の誤差は位相で発生します。ここでは、1.57 の位相は 1.49、3.14 の位相は 2.94、4.71 の位相は 4.58 として推定されています。このテストシグナルに 10% のランダム ノイズが追加されていることを考慮すれば、この結果は非常に良好です。
AR スペクトルアルゴリズムの詳細については、次の参考文献をご覧ください:
また、次の Burg アルゴリズムの情報も興味深いかもしれません:
固有解析スペクトルアルゴリズムの詳細については、次の参考文献を参照してください: