|
| サイトマップ | |
|
 |
| サイトマップ | |
|
このチュートリアルでは、2つのシグナルをスペクトル成分で比較するのに使用する FlexPro のスペクトル解析の機能を説明します。クロススペクトル、クロスピリオドグラム、コヒーレンス関数は2シグナル間の類似点や非類似点を評価する手段を提供します。通常このタイプの解析は同じ源から発生しているシグナルで使用されますが、必ずしもそうである必要はありません。データ長が同じ2つのシグナルであれば評価できます。
このチュートリアルでは、入力シグナルと出力シグナル間のフーリエ伝達関数もカバーしています。
もし、「フーリエ解析」をまだご覧でない場合は、このチュートリアルを最初にご覧いただくことをお勧めします。フーリエ解析のほとんどの原理がカバーされています。このチュートリアルでは、クロスフーリエスペクトル法を使用して異なる2つのシグナルを評価する際に生じる重要な項目のみに絞って説明します。
このチュートリアルでは、長さ 1024 のシグナルを2つ使用します。 1つ目は、ナイキスト帯域でパワーの等しい9つの正弦波からなる基準シグナルです:
2つ目のシグナルは、クロススペクトル解析で振幅、周波数、および、位相を変化させたときの影響を調べるために、その成分を以下のように変更します:
はじめの5つの成分は振幅 100% から 0% に線形で減衰します。続く2つ目の成分はナイキスト帯域の周波数を 0.1% と 1% 上方にシフトします。最後の2つの成分には -π と -π/2 の位相シフトがあります。
サンプリングレートは 5000 Hz です。したがって、ナイキスト周波数は 2500 Hz で、これが検出されうる最大周波数です。時間値はサンプリング増分 0.0002 で、0 から 0.2046 まで変化します。それぞれのシグナルに 10% ランダムのガウスノイズを加えます。これは最大ピークに対して約 -40dB のノイズフロアを発生させます。
ファイル > プロジェクトデータベースを開く コマンドを選択し プロジェクトデータベースに次のパス C:\Users\Public\Documents\Weisang\FlexPro\2021\Examples\Tutorials\Spectral Analysis.fpd を指定するか、日本語フォルダ名で C:>ユーザー>パブリック>パブリックのドキュメント>Weisang>FlexPro>2021>Examples>Tutorials>Spectral Analysis.fpd を指定して開きます。Tutorials フォルダの Cross Spectral Analysis というフォルダーを開き、Data と名付けられた 2D ダイアグラムをダブルクリックして開きます。
これは両方のシグナルをあらわすグラフです。浮動小数点値は 1024 個です。
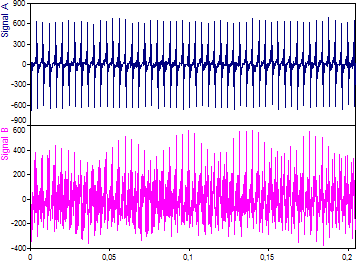
この時間領域から推測できることは、大きな相違点があるだけでなく、大きな類似点もあるということのみです。
ダイアグラムを閉じて、基準シグナルであるデータセット Signal A を選択状態にします。
「挿入」タブの [解析] から 「解析ウィザード」をクリックします。
「スペクトル解析」カテゴリから「フーリエ解析」を選択します。次に「フーリエスペクトル」を選択します。スペクトルプロシージャの中にはその結果が選択した複数のデータセットの順番に依存するものもある点に注意してください。"3.) データセットの割り当て:" リストに表示されている順番が正しいか常に慎重に確認してください。順番が正しくない場合は、そのエントリを選択肢リストの上にある矢印を使って上または下に移動してください。この例では Signal A が最初のエントリとなります。「次へ」をクリックします。
「スペクトルタイプ」に「振幅」を指定します。「ウィンドウタイプ」には「Cos3 最小サイドローブ -71dB W=3」を選択します。(「正規化」に「パワー」を指定します)「FFT長」が「データ長」または「1024」に設定されていることを確認します。「オプション」で 「最大ピークカウント」に値 9 を入力します。次に「ホワイトノイズ許容限界 %」を「なし」に設定します。ピーク上にラベルが表示されていない場合は 「ラベル切り替え」クリックして、振幅ラベルを表示します。
解析ウィザードのフーリエプロットは次のようになります:
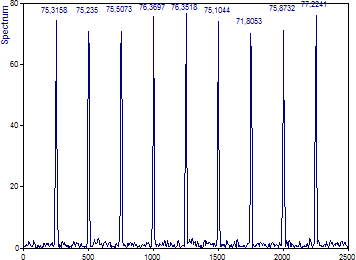
これらのピークは、通常どおり、フーリエチャネルの中心に配置されず、チャネルの中心からの高調波の変位も一定ではありません。変位が最小のとき、振幅は最大になります。また、ウィンドウをかけると一部のスペクトル情報がチャンネルを調整するために拡散することにも注意して下さい。ピークチャネルの振幅が実際の高調波の振幅の約 75% に過ぎないのはこれが理由です。
「キャンセル」をクリックし、データ Signal B に対して同じ手順を繰り返します。
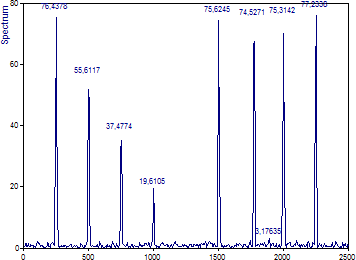
2 番目のスペクトルの唯一の明確な違いは、先頭のスペクトル成分の振幅が減少している点です。6 番目と 7 番目の成分の周波数のシフトは、もう少し微妙です。
「キャンセル」をクリックしてウィザードを閉じます。2つのデータ セット (Signal A と Signal B) を CTRL キーを押しながら選択状態にします。
「挿入」タブの [解析] から 「解析ウィザード」をクリックします。
「スペクトル解析」カテゴリを選択し、「2シグナルのスペクトルプロシージャ」を選択します。次に、「フーリエクロススペクトル」を選択します。「次へ」をクリックします。
個々のフーリエ解析と同じように、「スペクトルタイプ」で「振幅」を選択します。ウィンドウタイプ には「Cos 3 最小サイドローブ -71dB W=3」を選択します。(「正規化」に「パワー」を指定します)「FFT長」が「データ長」または「1024」に設定されていることを確認してください。「オプション」の「最大ピークカウント」に値 9 を入力します。ピーク上にラベルが表示されていない場合は「ラベル切り替え」をクリックして、振幅ラベルを表示します。
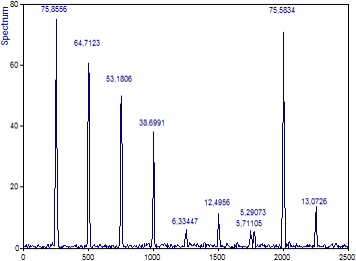
2 番目から 4 番目の成分の場合のように、振幅のみが変化する場合、クロススペクトル振幅は 2 つのスペクトルの間にあります。
5 番目の位置では、一方のシグナルには高調波があり、もう一方のシグナルには高調波がまったくありません。それでも、小さなピークが残っています。これは、この特定の周波数における基準となる高パワーのシグナル成分と2番目のシグナルのノイズ間のクロススペクトルです。なお、特定の周波数にピークが存在するからといって、必ずしも両方のシグナルに意味のある高調波成分があると推測できるわけではありません。この場合、最初のシグナルにのみ重要な高調波成分があります。
6 番目の位置では、2つのピークがナイキスト帯域のわずか 0.1% だけシフトした場合に何が起こるかがわかります。軽微ですが、小さなクロススペクトル特性が依然としてあります。2500 Hz をカバーするスペクトルで、わずか 2.5 Hz のシフトが見られます。
7 番目の位置では、周波数シフトはナイキストの 1% で、この例では 25 Hz です。クロススペクトル特性はこれで2つになります。2つは最初のシグナル成分の中心周波数にあり、もう1つは2番目のシグナル成分の中心周波数にあります。クロススペクトルシグナルがないという意味でこれらはノイズピークです。
8 番目の成分のように位相が π だけシフトすると、正弦と余弦でモデル化した場合と同じ違いになります。振幅のすべてがリカバーされます。ただし、位相シフトが最悪の場合、つまり9番目の成分のように π/2 になると、クロススペクトル振幅の多くが失われます。
個々の重なり合うセグメントを平均化して、周波数分解能を犠牲にして分散の少ないフーリエ推定値を生成するピリオドグラムと同様に、クロスピリオドグラムにも同じ原理を適用できます。
「クロスピリオドグラム」アルゴリズムを選択します。「振幅」が選択され ウィンドウの「タイプ」に「Cos 3 最小 Sidelobe -71dB W=3」が設定されていることを確認してください。「セグメント長」 は 「データ長の 1/4」 または「256」、「FFT長」は「セグメント長」または「256」に設定します。オーバーラップ は 50% に指定します。オプション で「 最大ピークカウント」 に値 9 を入力してください。ピーク上にラベルが表示されていない場合は 「ラベル切り替え」 をクリックして、振幅ラベルを表示させます。
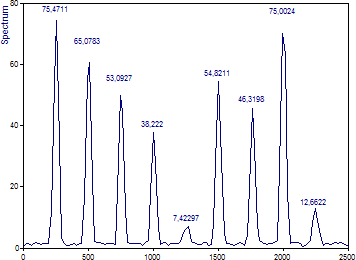
ピーク幅がはるかに広くなるのは、フーリエ分解能が単一セグメントのクロススペクトルの 1/4 しかないためです。この周波数分解能の低下は、この例では重要な要素です。
分散が減少したことはスペクトルがはるかにスムースになっていることから明らかです。最初の成分のクロススペクトル振幅がより正確に決定されます。5 番目の周波数ポジションの高調波とノイズのクロススペクトルは、低パワーのスムースなピークになります。
最も大きな違いは、6 番目と 7 番目の成分にあります。周波数解像度が低下したため、成分間に大きな重複が生じています。クロススペクトル振幅は 2.5 Hz のシフトによって 3 分の 1 未満に減少します。25 Hz のシフトでも、クロススペクトル振幅は周波数が完全に一致した場合の半分未満に減少します。
ここで、クロスピリオドグラムの解像度を向上させる手順を実行します。高ダイナミックレンジのクロスフーリエ解析 (一般的な非常に低パワー成分の検索) は実行しないため、周波数領域の解像度がそれほど低下しないウィンドウを使用します。また、データ長の半分のセグメントを使用して解像度を 2 倍にします。分散を改善するため、または、少なくともより滑らかなスペクトルを生成するために、オーバーラップを増やしてより多くのセグメントを平均化します。
ウィンドウの「タイプ」を「Cos2 ハニング -31dB W=2 」に、セグメント長を「512」に、FFT 長を「セグメント長」または 「512」に設定します。オーバーラップを 「90%」に変更します。
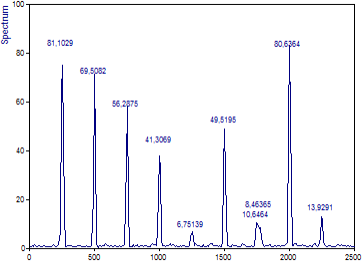
周波数が異なる 6 番目と 7 番目のコンポーネントでは、ピークがはるかに鋭くなり、クロススペクトルピークの大きさがはるかに小さくなっていることに注意してください。滑らかさはいくらか失われましたが、隣接するビンへの波及が少なくなったため、振幅はいくらか高くなっています。
複数のセグメントを使用すると、コヒーレンス スペクトルを生成することができます。コヒーレンスは、特定の周波数でスペクトル成分が類似している場合に 1 になり、シグナルが類似していないか完全に無相関である場合は 0 になります。これは、出力シグナルが非コヒーレントである、つまり、高調波周波数に差があるようなスペクトル領域を探すのに便利な方法です。
スペクトルプロシージャに「コヒーレンス」を選択し、スペクトルタイプに「コヒーレンス」を選択します。クロスピリオドグラムで行った設定はすべてそのままにしておきます。ピークラベルをオフにするには、[ラベルの切り替え] をクリックします。
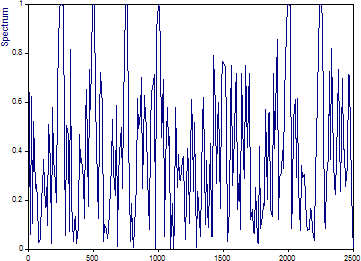
2つのシグナルの最初の成分の振幅は異なりますが、これは MSC (振幅の二乗のコヒーレンス) には影響しません。最初の 4 つの成分のコヒーレンスは 1 に達しているのが分かります。
5 番目の成分は、一方のシグナルには存在し、他のシグナルには存在しないため、ベースラインより上には何も表示されません。
6 番目の成分は、2つのシグナル間で周波数がわずか 2.5 Hz しか違いはありませんが、周波数が 25 Hz も異なる 7 番目の成分よりも高いコヒーレンスを持っています。また、この 7 番目の成分は一貫して低いコヒーレンスを生成することにも注意してください。
MSC も位相に依存しません。8 番目と 9 番目の成分は、位相シフトにかかわらず、コヒーレンス 1 を示します。
セグメントを複数使用する場合は、シグナルノイズ比のスペクトルを生成することができます。これは、スペクトル内の各周波数におけるシグナルノイズ比の推定値はコヒーレンス値を使用して生成されます。
スペクトルタイプに「シグナルノイズ比 dB」を選択します。
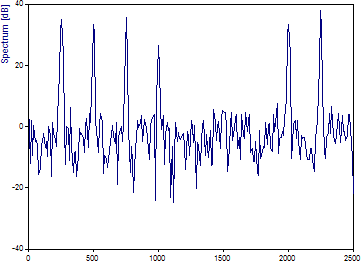
両方のシグナルに約 -40 dB のノイズフロアを生成したことはわかっています。ここでは、このノイズフロアより約 40 dB 上昇するピークを確認できます。コヒーレンスと同様に、振幅と位相を変化させた2つのコンポーネントは、完全な S/N またはそれに近い S/N を示しています。周波数を 2.5 Hz シフトした成分は S/N がわずかに改善されていますが、25 Hz シフトした成分はノイズと区別がつかないように見えます。
フーリエ伝達関数は、システムの伝達特性をあらわす周波数領域のマップです。この例では、2 番目のシグナルには、周波数シフトのある2つのインスタンスを除いて、各周波数で常に同じかそれより少ないエネルギーが含まれていました。
コヒーレンススペクトルや SNR スペクトルとは異なり、伝達関数は単一セグメントで計算できます。そのため、クロススペクトルプロシージャで最初に適用した設定を使用することにします。
「伝達関数」および「 スペクトルタイプ」に「dB」を選択します。ウィンドウのタイプ には「 Cos 3 最小サイドローブ -71dB W=3」 を選択します。「FFT 長」を 「データセット長」 または 「1024」に設定します。「ラベル切り替え」ボタンをクリックしピークラベルを消します。上のダイアグラムをクリックし「カーソルの切り替え」 (ダイアグラムの下のツールボックスの最初のボタン)をクリックします。
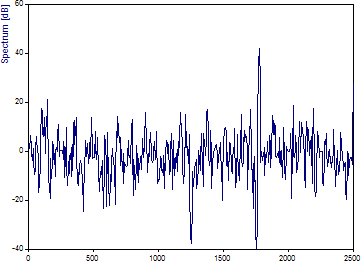
カーソルを最初の成分の位置である 250 Hz に設定します。値は約 0.17 ~ 0.18 dB です。カーソルを 500、750、1000 に設定すると、-2.5 ~ -2.6 dB、-6.0 dB、-11.7 dB が表示されます。
これらは、2 番目のシグナルにおけるこれらの高調波の振幅の 1/4、1/2、および 3/4 の減少に対応します。
なお、伝達関数の1250 Hz には深いヌルがありますが、これは、2 番目のシグナルにピークが全く存在しない点に注意してください。
また、伝達関数の 1750 Hz にも深いヌルがあり、ここでも出力シグナルにはピークがありません。また、伝達関数の 1775 Hz には鋭いピークがあり、ここで出力シグナルには鋭いピークがありますが、入力シグナルには何も存在しません。
現実のアプリケーションでは、上記セクションで使用した種類のシグナルに伝達関数を計算してもあまり意味がないことに注意してください。我々は、Signal B は LTI (線形時不変) システムの応答ではないことが容易にわかります。これは、LTI システムが既存のスペクトル成分の位相と振幅しか変化させないのに対し、Signal B は周波数をシフトしているためです。さらに、LTI システムの全体像を把握し、伝達関数を明確に定義するには、入力シグナルで LTI システムのすべてのモードを引き出す必要があります。このような入力シグナルには、たとえばホワイトノイズがあります。
これを実演するために、サンプルプロジェクトデータベースに追加のデータセット Input Noise とノイズデータにローパスフィルタを適用した Output Noise という名称のオブジェクトを用意しています。Transfer Function オブジェクトは、このローパスフィルターを反映するシグナルの伝達関数を計算するように既に設定されています。同じ名称のダイアグラムは、これを視覚化したものです。使用するローパスフィルターは、フィルタ特性がバターワース、次数が4、カットオフ周波数が 100 Hz です。
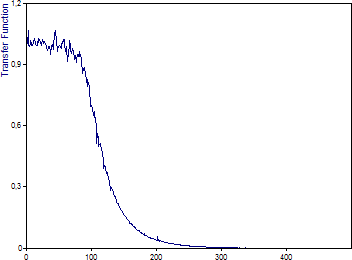
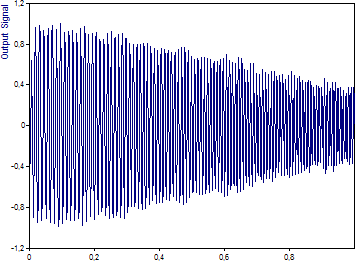
最後の演習として、入力シグナルに伝達関数を適用して、出力シグナルの推定値を求めます。周波数が 75 Hz ~ 125 Hz のチャープ サインである Input Signal オブジェクトを選択します。右クリックして「新規オブジェクトを挿入」をポイントし、「数式」をクリックします。次の数式を入力します: IRFFTn(FFTn('Input Signal') * 'Transfer Function')。 次に、実行をクリックして数式をテストします。1000 ポイントのシグナルが返されるはずです。OK をクリックして数式ウィンドウを閉じます。この数式の名称をもう一度選択状態にし、F2 キーをクリックします。次に、新しい名称 Output Signal と入力します。この数式は、入力シグナルのスペクトルを計算し、それを伝達関数で乗算します。出力シグナルのこの単純な計算が可能なのは、時間領域での畳み込みが周波数領域での乗算に等しいためです。スペクトルを乗算するときは、周波数カウントと周波数間隔が両方のスペクトルで同じになるように注意する必要があります。このチュートリアルをできるだけシンプルにするために、入力ノイズシグナルと入力チャープシグナルの両方のデータ長と等しい単一のセグメントから伝達関数を生成しました。重複するセグメントを平均化した場合、伝達関数はより滑らかになり、長さも短くなります。
周波数が上昇するにつれて振幅が減少する 1000 個の実数値を含むデータ セットが生成されます。カットオフ周波数 100 Hz は、入力のチャープシグナルのちょうど中央で到達します。予想どおり、そこでは出力シグナルの振幅が約 -3 dB 減衰します。