高調波推定チュートリアル

このチュートリアルでは、高調波モデリングと高調波歪み測定に関連する FlexPro のスペクトル解析機能を紹介します。

フーリエ解析

まだフーリエスペクトル解析チュートリアル と スペクトル推定チュートリアル をご覧になっていなければ、先にこれらをご覧になることをお勧めします。FlexPro の高調波推定の最初のステップは、フーリエ解析、ARスペクトル解析、固有値解析によって通常おこなわれる完全に自動化された周波数 (スペクトル) 推定です。

歪みとノイズのある高調波テストシグナル

このチュートリアルでは、長さ 1024 のシグナルを１つ使用します。このシグナルには基本波 (primary harmonic) が１つ、その周波数の整数倍の２次以降の高調波 (secondary harmonics) が４つあります。

• 100.0*sin(2π*x*250+π/4)
• 10.0*sin(2π*x*500+π/2)
• 1.0*sin(2π*x*750+π)
• 0.1*sin(2π*x*1000+3π/2)
• 0.01*sin(2π*x*1250+7π/4)

サンプリングレートは 5000 Hz 、ナイキスト周波数は 2500 KHz で、これが検出可能な最大周波数です。時間値は 0.0002 サンプル間隔で 0 から 0.2046 まで変化します。0.01% のランダムなガウスノイズを追加し、これにより、最大ピークに対して約 -100 dB のノイズ フロアが生成されます。

ファイル > 開く > 参照から下記のパスにあるプロジェクトデータベースを開きます。

または、日本語のフォルダ名で C: > ユーザー > パブリック > パブリックのドキュメント > Weisang > FlexPro > 2021>Examples>Tutorials>Spectral Analysis.fpd に移動します。Tutorials フォルダを開いたら、Harmonic Analysis サブフォルダを開いて、Data という名称の 2Dダイアグラムをダブルクリックして開きます。

これはシグナルのグラフです。 1024 個の浮動小数点値があります。

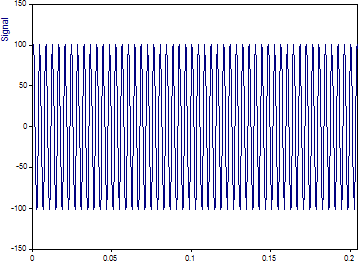
時間領域ではっきり分かるのは基本波のみです。２次以降の高調波は非常に大きな高調波歪みをあらわします。

高調波成分の数は、数えなくてもわかっていますが、まずは、このシグナルのフーリエスペクトルを調べます。

フーリエスペクトル

グラフウィンドウを閉じて、Signal データセットを選択状態にします。

挿入 [解析] > 解析ウィザードをクリックします。

スペクトル解析の中にあるフーリエ解析カテゴリを選択します。次に、フーリエスペクトルを選択します。「次へ」をクリックします。

スペクトルタイプ には「正規化 dB」を選択します。ウィンドウタイプ には「チェビシェフ」を選択し、ウィンドウ調パラメータに 4 を入力します。FFT 長が 16384 に設定されているか確認してください。最大ピークカウント オプションを選択し、5 を入力します。次に 「ホワイトノイズ許容限界 %」 を 「なし」 に設定します。ピーク上にラベルが表示されていない場合は「ラベル切り替え」 ボタンを dB レベルが表示されるまでクリックします。

解析ウィザードのフーリエプロットは次のようになります。

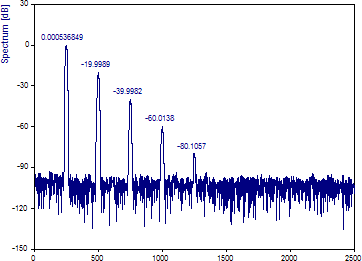
2次以降の高調波がフーリエスペクトルによってはっきりあらわれます。

周波数が表示されるまで「ラベルの切り替え」をクリックします。

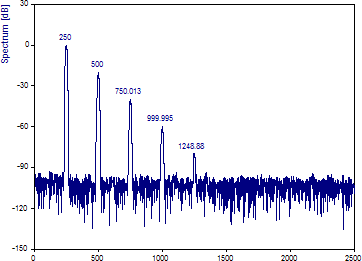
この最適化されたフーリエ スペクトルから、基本波と2次以降の高調波の周波数を正確に見積ることができます。

周波数識別のフーリエ手法

フーリエスペクトルで使用した条件は、フーリエ解析を周波数識別に使用する高調波推定プロシージャで自動的に実装される条件をあらわします。すべてのケースで、「チェビシェフ」データテーパーを使用し、その周波数領域の片側幅は自動的に設定されます。データ長が 256 以下の場合、この幅は 2 に設定されます。データ長が 1024 を超える場合、ウィンドウ幅は 4 に設定されます。これらの値の間で、このウィンドウ調整は -6+1.4427ln(n) で対数的に変化します。これにより、データ長が 512 の場合、周波数領域幅は 3 になります。データ長が 16384 未満の場合は、ゼロパディングを使用して、長さ 16384 の FFT が作成されます。

周波数識別のためにフーリエ解析を使用することに関連して、2つの注意事項があります。 1つ目は、データテーパリング、ゼロパディング、および、ビン補間を使っても、 AR または固有値解析よりも周波数推定の精度が小さくなる場合があることです。これは、データの長 1000 ポイント以下の近くにある場合に特に当てはまります。数百ポイントなど、データ長が非常に小さい場合、周波数識別のフーリエ解析は推奨されません。

同様に重要な問題は、スペクトルピークの大幅な上昇と減衰時にフーリエ解析では鋭いスペクトル特性が生じる場合があることです。この効果を最小限に抑えるためにチェビシェフウィンドウを選択しましたが、特に周波数推定値を改善するために実装されたゼロパディングでは、依然として発生する可能性があります。高調波解析では、ノイズ傾向をモデル化するためのいくつかの高調波が含まれることがあるため、シグナル成分のモデリング精度をさらに向上させるためには、高調波モデルの肩にあるピークが高調波モデルに大幅に登録されないようにすることが重要です。

以下は、上記と同じフーリエスペクトルですが、ウィンドウにブラックマン-ハリス -92dB を使用し、ピークを10個検出しています。

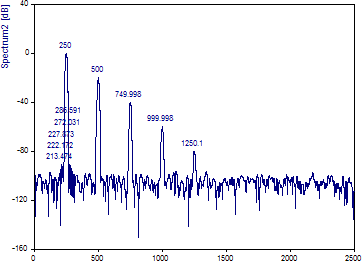
なお、追加された５つのピークはいずれも基本波のピークの肩に生じている点に注意してください。このような場合、追加された高調波をモデルノイズに含めることはできません。代わりに、このモデルでは高調波を５つしか含めないことが重要です。

高調波推定

高調波推定の目的は、狭帯域シヌソイドや減衰正弦波を使用してシグナルをモデル化することです。解析の結果は、振幅、周波数、位相、減衰正弦波の場合は減衰因子によって定義される高調波のセットです。

「戻る」をクリックします。「スペクトル解析」の中の「高調波解析」を選択します。次に、「高調波推定」を選択します。「次へ」をクリックします。「アルゴリズム」には「フーリエ」を、「モデル」には「シヌソイド」を選択します。「成分の数」に「最大カウントによる」を選択して 10 を入力します。「結果のタイプ」に「高調波成分」を選択します。「ラベルの切り替え」ボタンをクリックして振幅を表示させます。

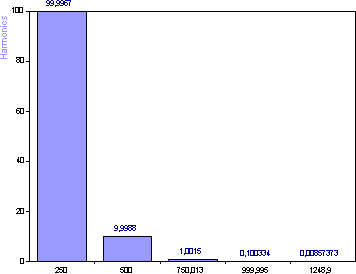
ラベルから振幅を読むことも可能ですが、これは良いグラフ表現ではありません。幅広いダイナミックレンジの振幅を適切に表示するには、対数スケールにする必要があります。

「次へ」をクリックして、ウィザードのステップ3に進みます。一番上のチェックボックスをチェックしてから、「高調波」 という名称の2Dダイアグラムを選択します。対数軸の y にチェックを入れます。 「戻る」をクリックして、ウィザードのステップ２に戻ります。

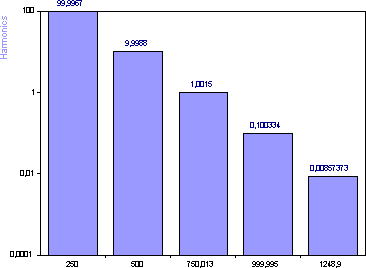
高調波モデリングのアルゴリズムは２つのステップからなります。フーリエステップは、スペクトル成分が存在する周波数を推定するためにのみ使用されます。フーリエスペクトルから得られた振幅やパワー情報は、高調波推定では使用されません。この例では、最も重要な周波数領域のスペクトル成分を持つ10の周波数の決定にフーリエ法を使用しました。ここにあらわされている高調波スペクトルは、時間領域線形最小二乗シヌソイドによる当てはめで作成されます。最初の4つの振幅は非常に正確に決定されます。5番目の高調波は誤差が10％を超えています。残りの高調波は、存在するノイズをモデル化することを目的としていました。ここではそうではありませんが、ホワイトノイズはすべての周波数に均一に分布しているため、高調波のカウントは、シグナルの実際の高調波のカウントに設定する必要があります。

フーリエスペクトルの視覚的結果からシグナルの5つのピークを適切に確認していますが、フーリエ周波数に基づいた高調波フィットではそれほど明確ではありません。シグナルとノイズの間に明確な境界はありません。

アルゴリズムに 「AR データマトリクス FB SVD」を選択します。モデルの「次数」を40に設定します。

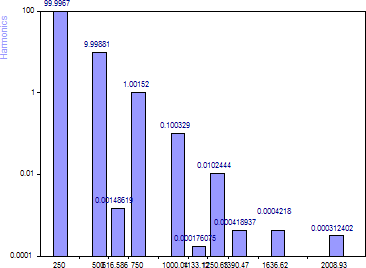
周波数識別に AR SVD アルゴリズムを使用すると、ノイズフロアの上には明らかに5つの成分があらわれます。さらに、周波数がより正確に推定されたため、線形シヌソイドフィットから得られる振幅もより正確になります。また、ランダムノイズの傾向の一部をとらえる際に予想されるように、追加の高調波が周波数全体に一層均一に広がっています。

アルゴリズムに「固有値解析 Root MUSIC」を選択します。

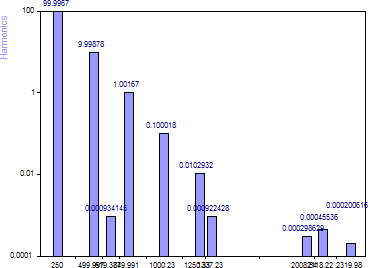
周波数識別に固有値解析 Root MUSIC を使用すると、ノイズフロアの上には明らかに5つの成分があらわれます。線形シヌソイドフィットから得られる振幅の精度は、AR メソッドの精度に非常に近いものです。

AR SVD メソッドでは、シグナルの固有モードを厳密に使用して周波数が推定されます。固有値解析では、ノイズの固有モードを厳密に使用して周波数が推定されます。指定したモデリングによって、どちらか一方がより正確になります。多くの場合、両方をチェックすることをお勧めします。なお 5つのシグナルの周波数は、両方の手順でほぼ正確に一致している点に注意してください。ノイズをモデリングするために追加した５つの高調波の重複ははるかに少なくなります。

高調波成分のパラメータ

ホワイトノイズは無相関になります。つまり、傾向や連続性が無いことを意味します。指定した不連続な周波数におけるノイズの振幅は、隣の周波数の振幅には影響を及ぼすことはありません。ノイズが完全に無相関であれば、追加の高調波を使用してノイズの傾向に当てはめを行ってもメリットはありません。

5つのシグナル成分のみをモデル化するには、最大カウントを5に設定します。

最もパワーの低い高次高調波 (振幅 0.01) は、もはや正確に推定されていないことに注意してください。実際、推定された振幅は、実際の値の 10 分の 1 近くまで低下しています。フィッティングで 10 個の高調波を指定したときには、ノイズのランダムな振動をモデル化するために 5 個の高調波を使用できましたが、現在は 5 個の実際のシグナル成分のみがフィッティングされています。ノイズは、この最もパワーの低い高次高調波のフィッティングに悪影響を及ぼします。

最大カウントを 10 に戻します。「次へ」をクリックします。ステップ 3 で、最初の 2 つの出力オプションを選択し、「完了」 をクリックします。「高調波推定」をダブルクリックします。

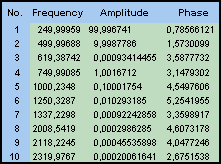
5 つのシグナル成分の周波数、振幅、位相は、非常に正確に推定されています。高調波モデリングでは一般に、分数誤差が最も小さいのは周波数 (frequency)、次に振幅 (Amplitude)、最も高いのが位相 (Phase) の分数誤差になります。振幅誤差はその中間です。指定した成分のパワーが高いほど、その高調波を定義するパラメータの精度は高くなる傾向があります。

高調波歪み

THD（全高調波歪み）は、基本波の振幅に対する高調波周波数のパワーの合計、または、振幅の二乗の平方根との比です。

従来、THD の測定には FFT が使用されていましたが、ウィンドウ処理によってスペクトル成分が隣接するビンに漏れ出したり、ウィンドウ処理されていないフーリエスペクトルを使用するときにスペクトル漏れが発生したりするため、FFT を使用して正確な THD を計算することは非常に困難です。このことは特にノイズを除外して高次の高調波のみを含める場合に該当します。

FlexPro の高調波モデリングでは、真の THD を正確に推定することが可能になります。このテストシグナルの正しい THD は sqrt(10²+1²+0.1²+0.01²) / 100 であることがわかっています。これは 10.05% です。

高調波モデリングに使用したこの設定は、高調波歪みスペクトルにも適しています。

Signal データセットを選択状態にします。

挿入 [解析] > 解析ウィザードをクリックします。

「スペクトル解析」の「高調波解析」カテゴリを選択します。次に、「高調波推定」を選択します。「次へ」をクリックします。

アルゴリズムに「固有値解析 Root MUSIC」、モデルに「シヌソイド」を選択します。成分の数に「最大カウントによる」を選択して 5 を指定します。「結果のタイプ」に「高調波ひずみスペクトル％」を選択します。「ラベル切り替え」ボタンをクリックして歪みの％を表示させます。

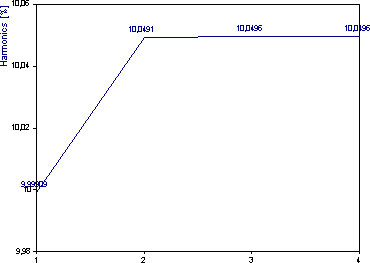
成分の数は x 軸に表示されます。成分 2 では、最初の高次高調波と基本波間の高調波歪みがプロットされます。成分 3 では、最初の高次高調波と 2 番目の高次高調波に関連する高調波歪みがプロットされます。したがって、THD (ノイズなし) は成分 4 の値です。10.0497 という値は、正しいことがわかっている 10.0504 の値に非常に近いです。成分の数を再び 10 に設定してみると、追加のノイズ 成分は THD に対して大きく影響しないことがわかります。

「完了」をクリックして解析ウィザードを閉じます。