 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
本チュートリアルでは、FlexPro のフーリエスペクトル解析の機能について説明します。この例では、広義の定常シグナル (wide sense stationary signals) 中の非常に低パワーの成分の特性を調べ、分散を抑えたスペクトルを推定します。
本チュートリアルでは、ナイキスト帯域でパワーの等しい4つの基準正弦波と、それらの間に配置する3つの低パワーの正弦波からなるシグナルを使用します。低パワーの成分は、基準正弦波との差がそれぞれ -40 dB, -50 dB, -60 dB であるとします。その後、ノイズフロアが約 -75 dB になるようなホワイトノイズを加えます。このテストの目的は、これら3つの低パワー成分の周波数とパワーを正確に見積もることです。2つ目のポイントは、これらの成分の位相情報を回復することです。
4つの基準正弦波と3つの低パワー正弦波を以下のように定義します:
x (時間) 値は、サンプル増分 0.0001 で 0 から 0.1 の範囲で変化します。従って、ナイキスト周波数は 5000 になります (つまり、サンプリング周波数 10000 の半分)。4つの基準正弦波は、このナイキスト帯域に広がります。最初の低パワー正弦波 (-40 dB) の振幅は基準正弦波の 1%、パワーは基準正弦波の 0.01% です。次の低パワー正弦波 (-50 dB) のパワーは基準正弦波の 0.001% です。最後のテスト正弦波 (-60 dB) の振幅は基準正弦波のわずか 0.1%、パワーは 0.0001% です。0.15% のガウスノイズを加えて、約 -75dB のホワイトノイズフロアを作成しました。従って、スペクトル解析をうまく設計できれば -60 dB 成分でも分解できます。
ファイル > 開く > 参照から下記のパスにあるプロジェクトデータベースを開きます。
または、日本語のフォルダ名で C: > ユーザー > パブリック > パブリックのドキュメント > Weisang > FlexPro > 2021>Examples>Tutorials>Spectral Analysis.fpd に移動します。Tutorials フォルダを開いたら、Fourier Spectral Analysis サブフォルダを開いて、Data という名称の 2Dダイアグラムをダブルクリックして開きます。
このシグナルのグラフは以下のとおりです。浮動小数点値が 1001 個あります。
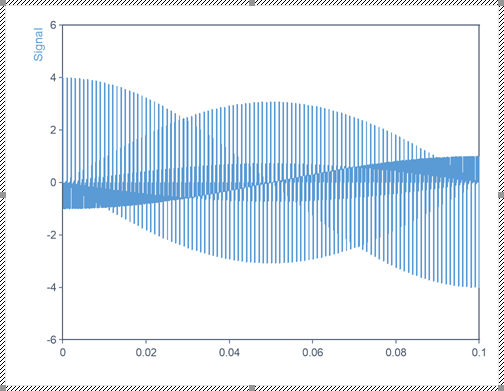
ダイナミックレンジの大きいフーリエスペクトル解析では、ほとんどの場合、データテーパリング窓を使用します。その理由を確認するために、まず、窓関数をかけない基本的な FFT を調べることにします。
ダイアグラムを閉じて、データセット Signal を選択状態にします。
挿入 [解析] > 解析ウィザードをクリックします。
「スペクトル解析」の「フーリエ解析」を選択します。「フーリエスペクトル」アイコンをクリックします。「次へ」をクリックします。
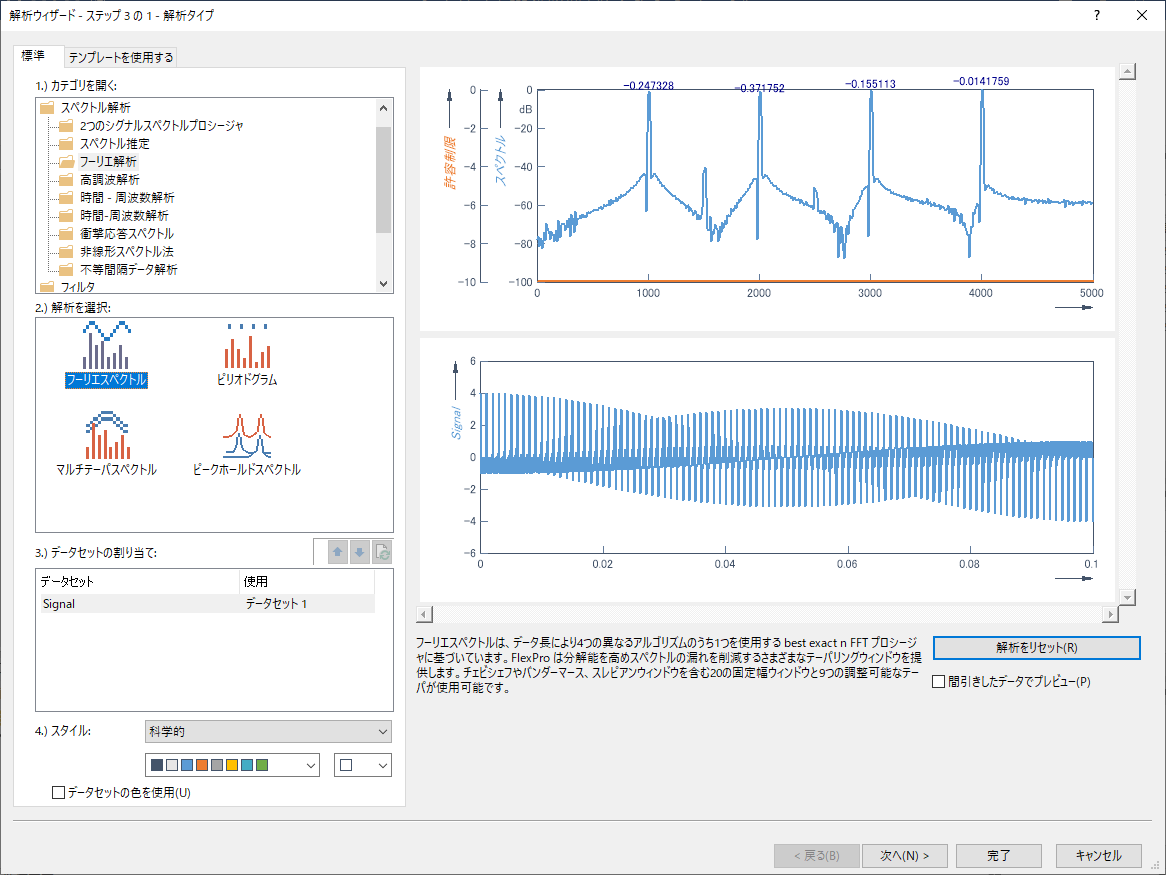
解析ウィザードのステップ2には、最適な解析を実現するために複数のプロシージャを最適化したり比較できるインタラクティブなダイアログが用意されています。それでは、まずはじめに、窓関数をかけないフーリエスペクトルを調べることにしましょう。
なお、「スペクトルプロシージャ」には「フーリエスペクトル」がチェックされている点に注意してください。解析ウィザードのステップ1で「スペクトルプロシージャ」を選択しても、その内容は、ステップ2で変更することができます。
「スペクトルタイプ」に「正規化 dB」を選択します。
これにより、スペクトルの最大ピークが 0 dB に正規化されます。その他のピークは、いずれも負の値をとります。ピークが -3 dB であればそのパワーは 0 dB のピークの半分になり、ピークが -6 dB であればその振幅が半分になります。
「ウィンドウタイプ」に「矩形 -13dB W=1」を選択します。
FlexPro のスペクトル解析モジュールでは、固定幅 (調整不可) の全てのデータテーパーが、それぞれの名称、dB 単位のサイドローブ減衰、片側フーリエ領域のピーク幅でリスト化されています。矩形窓は、すべてのデータ要素に1を掛けるので窓関数をかけないのと同じになります。
「FFT 長」には「データ長」または「1001」が設定されていることを確認してください。
「ゼロパッド」の情報フィールドには、ゼロによる埋め合わせが行われていない 0 が示されています。
「オプション」で「最大ピークカウント」を選択し、その値に 7 を入力します。
解析ウィザードには、スペクトルのピーク情報が自動的に出力されます。このオプションを 7 に設定すると、最大パワーをもつ7つのピークが出力されることになります。なお、「最大ピークの下の dB 閾値」を設定することも可能です。このデータセットでは、閾値として -65 dB を容易に設定できます。
「ホワイトノイズ許容限界%」には「なし」を設定します。
本チュートリアルの後半では、このシグナルに許容限界テストを実施します。
もし、上記の各ピークにラベルが表示されていない場合は、振幅ラベルが表示されるまで「ラベル切り替え」ボタンをクリックしてください。
「ラベル切り替え」では、幾つかの状態を切り替えることができます。ボタンを押すごとにスペクトルの Y 成分 (この場合は「正規化 dB」)、X 成分 (常に周波数) が切り替わります。また、ピーク情報を無しにすることも可能です。
解析ウィザードのフーリエプロットは以下のようになります:
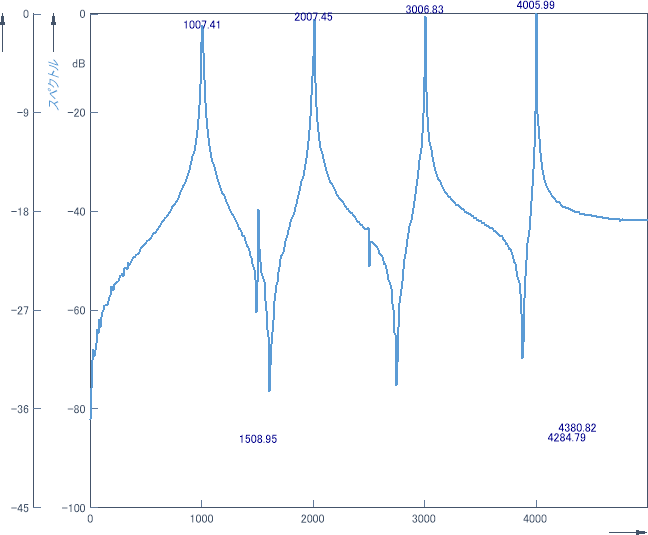
FFT 計算では、可能な限り高速な FFT アルゴリズムを使用してデータを正確に変換します。この事例では、Prime Factor FFT アルゴリズムを使用していますが、これは、1001 件のデータを正確に処理する最も高速な FlexPro の FFT プロシージャーです。出力されるフーリエスペクトルには、4つの基準ピークが即座に検出されます。-40 dB のピークは観察できます。-50 dB のピークはわずかに兆候が認められますが、-60 dB のピークは認められません。FlexPro では、 ビンの補間に3 次スプラインを使用して FFT ピークの周波数を求めていますが、基準周波数 1005、2005、3005、および 4005 は正確には再現されていません。
これら4つの基準は、実質的に形状が異なるピークで構成されている点に注意してください。スペクトルのピークは、周波数が大きくなるほど鋭くなっていますが、これは、スペクトルが隣接するビンに漏れているもので、周波数によるものではありません。高調波はスペクトル周波数のビンの中心に近いほど、FFT の周波数応答は鋭いものになります。
上のプロットを選択して、「カーソルの切り替え」ボタンをクリックします。カーソルを最初のピークに移動します。
最初のピークの実際の周波数は 1005 ですが、FFT のビンである周波数 999 と 1009 の範囲内にあることを確認できます。4番目のピークの実際の周波数は 4005 ですが、周波数4006 の FFT ビンとほぼ一致していると言えます。周波数がちょうどビンの中心になければ、高調波を単一の FFT チャネルで完全にあらわすことはできません。
「カーソルの切り替え」ボタンをもう一度クリックしてカーソル機能を無効にしたら、FFT 長を 8192 に変更してください。
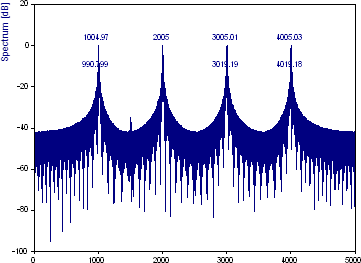
これににより、ゼロパディングを使用して FFT のサイズが増加します。スペクトルの周波数はこのとき約8倍に増加します。このビンによる補間で基準周波数が正確に決定されるようになりますが、ベースラインにある3つの低パワー成分は失われます。ゼロパディングの使用によりデータストリームに不連続性が生じるので、スペクトル漏れは増加します。
「FFT 長」フィールドに 2000 を入力します。更新を行う際は、Tab キーを押して編集フィールドを移動してください。
これにより、正確に 5 Hz 間隔の FFT が生成されます。このとき、7つの正弦波の周波数はいずれも、FFT ビンのちょうど中央になります:
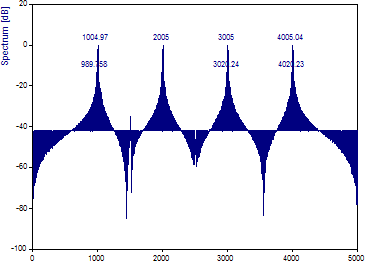
スペクトルのピークはインパルス関数になりましたが、ゼロパディングによるスペクトル漏れは、3つの低パワー成分をマスクするには充分です。データテーパリング窓を使用せずに低パワー成分を分解することはできません。
データテーパリング窓では、データストリームの両端にあるデータ値の大きさがどちらもゼロに減少します。これにより、データストリームの中心にあるデータへの影響が増大しますが、これによりデータの境界にある不連続性は除去されます。データをラップアラウンド形式で見ると、2つの端の接続部分に連続性があることを確認できます。
フーリエ領域にデータテーパリング窓を追加する影響はゼロではありません。データテーパリング窓には全てのスペクトルピークの幅を広げる周波数応答があるため、分解能が低くなります。また、低パワーの高調波もこれにより加わります。データテーパリング窓のメリットは、スペクトル漏れを大幅に軽減できることです。これにより、ゼロパディングによる任意の尺度を利用できるようになります。
FlexPro で窓関数を使用する場合、パワーの正規化がおこなわれます。窓関数をかけたフーリエスペクトルのパワーは、窓関数をかけないものと同じです。一方、パワーが同じに保持されても、スペクトルのピークの高さは、窓関数をかけたことである程度の減衰を示します。データテーパリング窓を使用する場合、正規化された dB スケールから相対的にパワーを判断することは可能ですが、振幅やパワーの絶対値をスペクトルピークの高さから直接読み取ることはできなくなります。
ウィンドウタイプを「Cos4 ブラックマン - ハリス -92dB W=4」に変更し、FFT 長を 8192 に指定します。
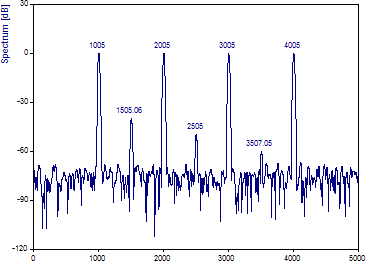
「ラベルの切り替え」をクリックしてラベルにスペクトルの大きさを表示します。
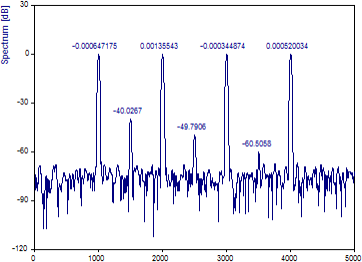
この「ブラックマン - ハリス」窓は、ダイナミックレンジの高いフーリエ解析でよく利用されるもののひとつです。4つの基準ピークの周波数とパワーはいずれも正確にマッピングされています。低パワーの3つのピークについても周波数とパワーの両方の特性があらわれています。
なお、厳密に 0 dB のピークは存在しない点に注意してください。ゼロ dB の正規化が行われるのは実際のスペクトルの値に対してです。レポートされるピークの値は、ビン補間されたものであるため、パワーの最大ピークは 0 dB よりも少し上回るのが一般的です。
適切なデータテーパリング窓を選ぶには訓練が必要です。FlexPro には、プロパティが固定された20種類の窓関数と、パラメータを調整することでプロパティを変更できる9種類の窓関数が用意されています。
選択リストのパラメータ W として表記されたメインローブの幅は、周波数分解能に直接関係します。メインローブの幅が 3 の窓関数の周波数分解能は、窓関数をかけないフーリエスペクトルの 1/3 しかありません。選択リストにはサイドローブ値も表記されています。これは、メインローブより小さいサイドローブの最大ピークで dB 単位の大きさです。このサイドローブ値が大きいほど、高パワー成分の周波数に近接する低パワーのピークを分解できる可能性が高くなります。窓関数を選択するもう一つの要因はロールオフ値です。ロールオフ値が大きいほど、スペクトルの主ピークより遠くにある低パワー成分を分解できる可能性が高くなります。サイドローブの値はスペクトル漏れが生じる全体の尺度で、スペクトル漏れの分散の仕方を指定するのがロールオフ値です。
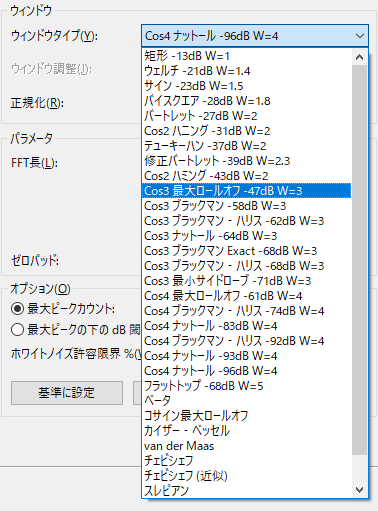
第1のトレードオフは、分解能とダイナミックレンジです。これは、メインローブの幅で決まります。第2のトレードオフは、隣接するピークと間隔の離れたピークの分解能です。これは、サイドローブとロールオフ特性によって決まります。
「チェビシェフ」窓は、指定したサイドローブ水準で最も鋭いスペクトルピークを出力します。パワー水準が異なり間隔が密な成分を分解するのに優れたテーパリング窓のひとつです。「Cos 最大ロールオフ」窓は、周波数領域で最速のコサインベースの減衰を出力します。これにより、スペクトルの主ピークからある程度離れた位置にある非常に低パワーのピークを分解できるようになります。「カイザー - ベッセル」窓は、これら2つの両極端の有効な妥協点となる非常に優れた調整可能な窓関数です。
「フラットトップ」窓は、ユニークな特性を示します。この窓関数のメインローブの最大幅は 5 ですので、スペクトル分解能は比較的低いものになります。ただし、このメインローブの最大幅は、ある周波数ラインから隣接する左右の周波数ラインまでの全帯域でほぼ同じ値になります。従って、メインローブの最大値は、幅が広く平坦なピークになります。この窓関数は、狭帯域のシグナル成分、すなわち、スペクトル内の個々のピークのパワーや振幅を測定するのに適しています。メインローブの最大値が特殊なタイプであることから、ピークが2つの周波数ラインの間にあってもその高さは実際にはその位置とは独立したものになります。
FlexPro では、あるシグナルのピークが統計的に有意であるか否かを確認するためにピークに基づく許容限界が出力されます。この基準はホワイト (正規分布) ノイズです。95% 許容限界は、個別のランダムノイズシグナルが20個あるとすれば、そのうち厳密にランダムな偶然で最大ピークの高さに達するものは1つしかないような水準です。同様に、99.9% 許容限界は、個別のランダムシグナルが 1000 個あるとすれば、そのうち最大ピークの高さに達するものは1つしかないような水準です。
FlexPro の許容限界は、プログラム内の実際のアルゴリズムや調整機能を使用した広範なモンテ・カルロ試験に基づくものです。この事例では、FlexPro の各窓関数毎に個別の許容限界モデルを使用します。調整可能な窓関数では、3D サーフェスモデルを使用します。このアプローチでは、窓関数を使用する際に生じるピークの高さの減衰が組み込まれるため、全ての n (データ数)、全ての窓関数、および、全ての窓関数の調整パラメータについて正確な許容限界が出力されることになります。
「ホワイトノイズ許容限界」を 99.9% に変更します。
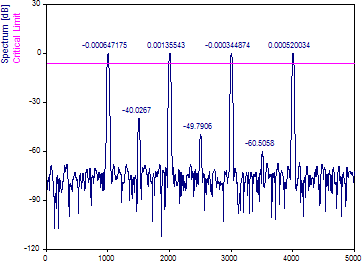
このデータセットでは、 99.9% を超える信頼度で最大ピークが有意であることが示されています。この検定では、最大パワーのスペクトル特性のみがガウスノイズと比較されます。ここから他のピークに関して結論を引き出すことはできません。
他の解析と比較するために、このプロットを「基準」として残しておきましょう。
現在の解析を基準として残すには「基準に設定」をクリックします。
下段のデータプロットが基準に置き換わります。なお、許容限界とピークはこの基準には含まれない点に注意してください。
低分散のスペクトルパワー推定を行う場合の FlexPro のスペクトル手法を紹介します。ここでは、パワー測定の精度を最優先するものとします。
FFT の分散は、データ長を増やしても減少しません。それどころか分散は一定で、分散の平方根 (標準偏差) はそのシグナルに含まれるパワーの平均とほぼ等しくなります。FFT ベースのスペクトル推定の分散を減らすには、アンサンブル平均 (集合平均) 法 (ensemble averaging) と直交テーパ法 (orthogonal taper) を使います。
FlexPro には、分散を減らしたスペクトルを推定するために利用できる2種類のフーリエプロシージャーが用意されています。
最初に紹介するのは「ピリオドグラム」です。定常なデータシリーズの場合、データの全シーケンスのそれぞれの部分は、いずれも同じスペクトル特性になります。この特性から、一連の FFT を合計することで、より分散を軽減したスペクトルを推定できるようになります。この FFT 系列は、指定した重なりの尺度でデータシーケンス全体を移動するスライディング窓 (より小さいサイズのセグメント) 内で作成します。FFT のサイズを小さくすればそれだけ分解能が低下します。最終的に推定するスペクトルの分散を減らすことの代償として分解能が犠牲になります。
「スペクトルプロシージャ」」で、「ピリオドグラム」オプションを選択します。「スペクトルタイプ」には、「正規化 dB」を引き続き使います。「ウィンドウタイプ」に「チェビシェフ」を選択し、「ウィンドウ調整」(片側フーリエ領域の幅) に 4.0 を設定します。必要な場合は、「セグメント長」をデフォルトの「データ長の 1/4」に変更します。FFT 長には 4096 を指定し、「% の重なり」を 90 とします。ピーク上にラベルが表示されていない場合は、「ラベル切り替え」ボタンをクリックして振幅のラベルの表示に切り替えてください。
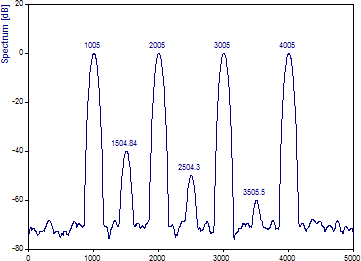
「ラベル切り替え」ボタンをクリックして dB スペクトル密度を表示します。

デフォルトの「セグメント長」 データ長の 1/4 (=250) と、「% の重なり」 90 を使うと、31 に分かれたセグメントを結合して分散の低いスペクトルが生成されます。セグメント長は、データストリーム全体の 1/4 に過ぎないため、その分、周波数領域の分解能は低下します。ピリオドグラムの各ピークの幅が大きく広がるのはこれが理由です。しかし、合計してピリオドグラム全体を作成するフーリエスペクトルは 31 あります。このため、低パワーの3つのピークのパワー特性がより正確に出力されます。
ここでは、全周波数にわたって一定のホワイトノイズフロアが分布していることから「チェビシェフ」窓を使いました。ロールオフ特性が大きい窓関数についてはメリットはありません。もし、レッドノイズ (周波数の増加に応じて減衰するノイズ) が分布している場合であれば、「ベータ」や「Cos 最大ロールオフ」といったロールオフ値が非常に大きい窓関数を使うのが良い選択となります。
セグメントサイズとオーバーラップを最適化する試みは、必ずしも有意義な作業になるとは限りません。一般にセグメントの数を増やしても分散が実質的に減少することはありません。通常「% の重なり」が 50-70 を超えれば、窓関数をかけるか否かにかかわらず分散はほとんど減少しません。
ここで、データテーパを使用すると振幅にどのような影響が及ぶかを観察してみることにしましょう。
「ウィンドウタイプ」を「矩形 -13dB W=1」(窓関数をかけない) 、「正規化」を「なし」、「スペクトルタイプ」を「振幅」に変更します。
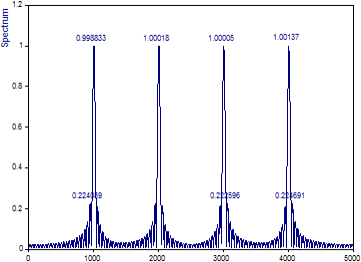
4つの基準正弦波の振幅 (いずれも 1.0) は、「% の重なり」が大きいことから非常に正確に復元されている点に注目してください。
「ウィンドウタイプ」を「Cos2 ハミング -43dB W=2」に変更してみましょう。

ハミング窓は、片側フーリエ幅が2のサイドローブが最小になる余弦級数窓です。ピークの振幅が約 50% に減少している点に注目してください。スペクトルが個別のピークで構成されていれば、その低減は選択した窓関数によってのみ変わりますので、非常に容易に補正できます。
「正規化」を「振幅」に変更します。
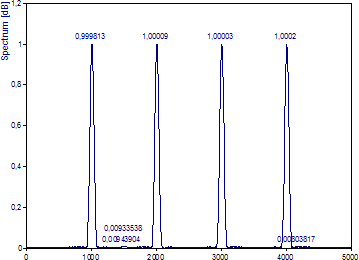
ピークの振幅は、シグナル中の基準振動の振幅と全く同じです。振幅の正規化には、正規化因子に選択した窓関数の利得、すなわち、窓関数を二乗した値の合計をデータ数で割ったものを使用します。この種類の正規化では、スペクトル内のパワー合計と時間シグナルのパワー合計が必ずしも同じになるわけではない点に注意してください。同じにする必要があれば、正規化の種類に「パワー」を選択できます。
「ウィンドウタイプ」を「Cos3 最小サイドローブ -71dB W=3」に変更します。
この窓関数の記述にリストされているサイドローブの減衰 -71dB は、低パワーの3つのピークを回復するのに充分なダイナミックレンジであることを示唆しています。
「スペクトルタイプ」を「正規化 dB」に変更します。
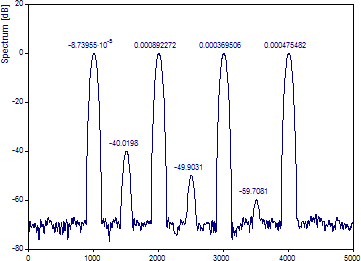
このデータテーパを使って、狭帯域にある3つの低パワー成分が実際に分解されているのが分かります。また、スペクトルのピークも、最初に評価した幅4のチェビシェフテーパに比べて、この幅3の窓の方が鋭くなっています。この事例では重要ではありませんでしたが、スペクトル特性が密集したものである場合は、サイドローブ dB がデータのノイズフロアを下回る窓の使用が必要があることがあります。調整可能な窓関数は連続的であるため、フーリエ幅を任意の小数に設定できる点に注意してください。
「ウィンドウタイプ」を「チェビシェフ」に変更して、片側フーリエ幅の「ウィンドウ調整」を 2.9 に設定してみましょう。
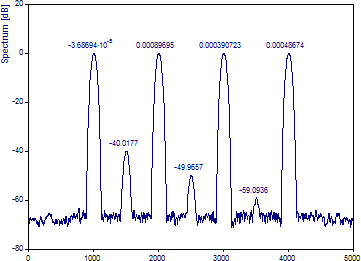
これにより、スペクトルのピーク幅を最小限に抑えた最適に近いデータテーパがあらわされます。これらのピークは、ノイズフロアを上回る最低のパワー成分を分解するための最小幅になっています。ただし、これらは必ずしもピリオドグラムにとって最適な設定であるとは限りません。改善された分散の一部を犠牲にすれば、より鋭いスペクトルにすることができます。
「セグメント長」のドロップダウンリストから 500 を選択します。「% の重なり」は 90 のままです。
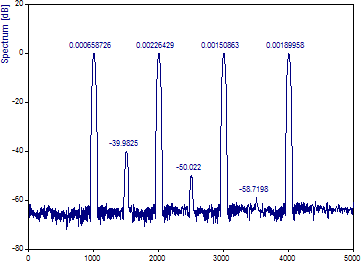
これらの設定を使えば、長さ半分のフーリエスペクトルを11個使用してピリオドグラムが生成されます。
なお、スペクトルのピークがはるかに鋭くなっている点に注意してください。同様にスペクトルのノイズ領域における分散が大きいことと最低パワー成分における回復が非常に弱いことも明白です。
分散を抑えたスペクトルを生成する FlexPro の2つ目のフーリエオプションは、マルチテーパー プロシージャです。マルチテーパー プロシージャでは、一連の直交テーパーをデータに適用し、それぞれのスペクトルを何らかの方法で平均化し複合スペクトルを生成します。それぞれ独立したスペクトルにデータストリームの一部しか使用しない segmented-overlapped アプローチとは異なり、マルチテーパプロシージャは個々のテーパーにデータ全体を使用します。
マルチテーパープロシージャは、さまざまなデータテーパーウィンドウから得られたスペクトルを平均化するのと似ています。この場合、ある程度の冗長性が生じます。それはテーパーウィンドウ間の相関性が高いからです (すべてのピーク形状が非常に共通している) 。マルチテーパースペクトルの生成に使用する直交テーパーは、従来のデータテーパーとは異なり相関性がありません。従来の形状を持つのはデータテーパー ウィンドウの最初のものだけです。
異なるテーパーから得られるスペクトルは、高調波成分で一般に見られる中心ピークを生成しません。最初のテーパーのみが、成分の高調波周波数で中心ピークを生成します。他のテーパーは、周波数がわずかに上下にシフトしたスペクトルピークを生成します。それぞれのスペクトルは、各成分の全体的なスペクトルピークの形状に寄与します。
マルチテーパー解析のメリットは、フーリエ分解能を犠牲にせず、データの両端で情報が失われないことです。確かに境界付近の情報は最初のテーパーでは失われますが、後続のテーパーには含まれ、強調されます。各成分に関連付けられたスペクトルピークの形状により、相対的なパワーを容易に決定できるようになります。デメリットは、各成分に割り当てられたスペクトルピークの形状からは周波数の鮮明な分解能は得られないことです。
マルチテーパープロシージャでは、結果として得られるスペクトルのパワーの正規化が常に実行されます。したがって、「正規化」リストから「なし」と「パワー」を選択しても結果は同じになります。正規化に「振幅」タイプを選択すると、ピリオドグラムと同じように使用して、スペクトル内のピークの振幅の減衰を補正できます。この正規化係数は、「ウィンドウの数」と「ウィンドウの幅」の関数として経験的に決定されます。
スペクトルプロシージャーに「マルチテーパースペクトル」を選択し、スペクトルタイプに 「正規化 dB」を選択します。片側フーリエ幅 (「ウィンドウ調整」) を 3.0 に設定します。DPSS ウィンドウの数には「最大値」または 5 を入力します。FFT 長を 4096 に設定します。「ラベルの切り替え」をクリックしてピーク上に周波数を表示させます。
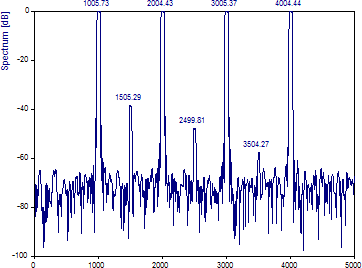
スペクトルピークの形状がマルチテーパースペクトルの特徴のテーブルトップ型である点に注目してください。この形状により、スペクトルの相対的なパワーを視覚的に識別することは容易ですが、各ピークを定義するスペクトルピークの形状の中心周波数を特定するのは困難です。FlexPro では、F 比スペクトルのピーク位置を使用してピークの周波数を割り当てます。F 値は有意性の尺度であり、分散とは直接関係ありません。
「ラベルの切り替え」をクリックして、dB スペクトル密度を表示します。
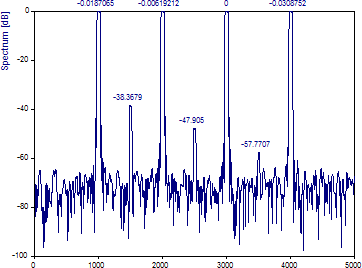
なお、ピリオドグラムとは異なり、直交テーパーのスペクトルを平均化することは、ノイズフロアを滑らかにするわけではない点に注意してください。
マルチテーパーのスペクトルピークの形状には明確なピークがないため、スペクトルの最大値が必ずしも高い精度で決定される訳ではありません。これが、正規化されたスペクトルにおいて3つの低パワーピークのすべてが +2 dB ずれている理由の 1 つです。
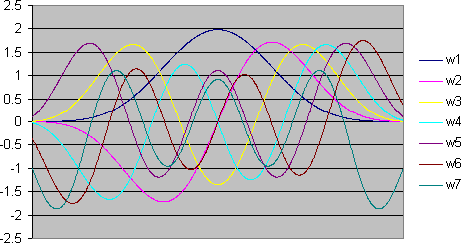
マルチテーパースペクトル解析における注意事項は、サポートされているテーパーの最大数を使用することです。片側フーリエ幅(「ウィンドウ調整」)が 3.0 の場合、FlexPro は最大 5 つのテーパーをサポートします。幅が 4.0 の場合、最大 7 つの DPSS テーパーを使用できます。個々の DPSS テーパーのダイナミックレンジは、シーケンスが進むにつれて減少します。最初の DPSS テーパー (DPSS プロットの w1) は優れたデータ ウィンドウであり、シーケンスの最高のダイナミックレンジを提供します (これは、フーリエおよびピリオドグラム手順の Slepian 調整可能ウィンドウです)。DPSS シーケンスの後続の各テーパーでは、ダイナミックレンジが減少します。広いダイナミック レンジが必要な場合は、シーケンスの最後の 1 つまたは 2 つのテーパーを除外するのが最適です。例えば、フーリエ幅 3 の設定の場合、合計 3 または 4 のテーパーが適切な選択となる可能性があります。フーリエ幅 4 のスペクトルの場合、5 のテーパーが最良の結果をもたらす可能性があります。
「DPSS ウィンドウの数」を 3 に変更してみます。
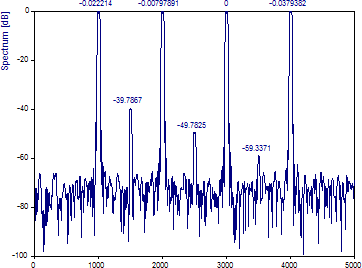
スペクトルのピークがかなり正確になっている点に注目してください。
「DPSS ウィンドウの数」を 5 または最大値に変更します。正規化に「パワー」を設定し、スペクトルタイプを「振幅」に変更します。
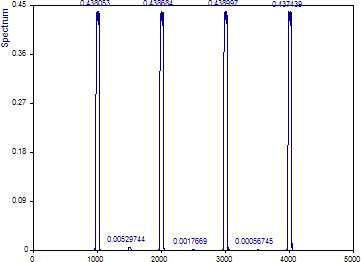
フーリエ幅 3 のデータテーパーを持つピリオドグラムの場合、振幅の減衰は約 24% でした (実際の振幅の 76% がピークチャネルに存在していました)。フーリエ幅 3 のマルチテーパーの場合、減衰は 56% とはるかに大きくなります (マルチテーパースペクトルのピーク形状のプラトーには実際の振幅の 44% しか現れません)。
「DPSS ウィンドウの数」を 3 に変更してみます。
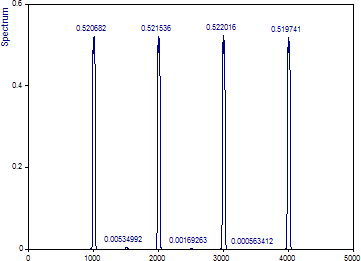
スペクトル減衰は、マルチテーパー解析のフーリエ幅に応じて変化するだけでなく、シーケンスで使用するテーパーの数によっても大きく影響を受けます。最初の 3 つの Slepian テーパーのみを使用する場合、振幅の減衰は約 48% ですが、最大 5 つのテーパーを使用する場合は 56% になります。
正規化のタイプに「振幅」を選択すると、減衰は完全に補正されます。
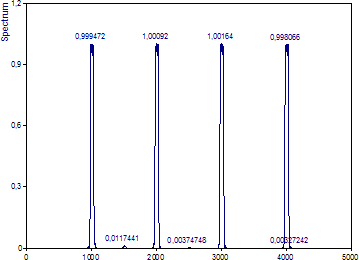
(1) データがシグナルの長さ全体にわたって広義の定常性 (WSS) であることを確認します。サンプル全体でスペクトル情報が変化しないことを確認するには STFT または CWT 解析を使用します。データストリームの両端の情報からうける影響はデータテーパリングによって大幅に減少します。これは、サンプル内の最も早い時間と最も遅い時間のデータが受ける影響を安全に強調しない場合にのみ実行します。
(2)スペクトル漏れを低減しながら高ダイナミックレンジのフーリエ解析を実現するには、通常、データテーパリングによるアプローチを使います。データテーパリングでは、スペクトルの振幅とパワーは減衰するので、これらを直接読み取ることができない点に注意してください。パワーと振幅を正確に測定するには、振幅タイプに正規化を使用します。
(3)データ長が非常に長い場合、解析は周波数領域で高解像度で開始されます。この一部は、ピリオドグラムによる分散の低減と引き換えることができます。
(4) データ長に制限があり、解析の目的が周波数とパワーの両方を正確に推定することである場合、単一のフーリエスペクトルを使用する必要があるかもしれません。スペクトルのピークは可能な限り最大の解像度が保たれますが、ランダムノイズのピークがデータ内に占める割合が高くなるため、それだけ分散が大きくなります。フーリエスペクトルオプションは、特定のシグナルがノイズと異なるかどうかをテストするのに最適な方法でもあります。ピリオドグラムのウィンドウなしの場合に限り利用できるホワイトノイズの許容限界がこのウィンドウ解析で指定できるためです。
(5)同様に、データ長に制限があり、解析の目的が主にパワーを正確に特徴付けることである場合、とりわけ、境界付近の情報も含めデータ内のすべての情報を活用することが不可欠な場合には、マルチテーパースペクトルが最良の選択となる可能性があります。
(6) 3 つの解析法は、いずれも、多くのスペクトル解析問題に適用できます。FlexPro では、3 つのアルゴリズムすべてを 1 つのフーリエ解析オプションにまとめることで、方法の選択が簡単になります。さまざまな手順を並べて比較するには、参照オプションを使用します。場合によっては、3 つの方法すべてを使用することで、最適な解析結果が得られることがあります。
FlexPro の解析ウィザードで自動的に作成される各種オブジェクトを調べるために、フーリエスペクトルを作成します。
「スペクトルプロシージャ」では、「フーリエスペクトル」を選択します。「スペクトルタイプ」では、「正規化 dB」を選択します。「ウィンドウ タイプ」では、「カイザー - ベッセル」を選択し、「ウィンドウ調整」では 3.0 を入力します。FFT 長を 8192 に設定します。「最大ピークカウント」オプションを選択し、7 を入力します。次に、「ホワイトノイズの許容限界 %」 を 99 に設定します。周波数ラベルが表示されるまで、「ラベルの切り替え」をクリックします。「次へ」をクリックします。ステップ 3 で、3 つのオプションすべてをチェックし、「完了」をクリックします。
FlexPro プロジェクトデータベースに8つのオブジェクトが作成されます。
「スペクトル」は解析オブジェクトです。スペクトル解析を実行するオブジェクトがこれになります。このオブジェクトをダブルクリックすると、ウィザードによって作成された解析オブジェクトが開きます。
「許容制限」は、プロットで使用される許容制限を生成するための数式オブジェクトです。
「ピーク」は、プロットに表示するピーク情報を生成するための数式オブジェクトです。
「高調波推定」は、高調波解析レポートを生成する数式オブジェクトです。
「スペクトル」はウィザードによって生成されたフーリエ スペクトル プロットです。使用オブジェクトは、スペクトル、許容制限、ピークです。

「データ」は、オリジナルの時間領域データのプロットです。
「高調波推定」は、最大ピーク数 7 で指定された 7 つの狭帯域コンポーネントのスペクトル情報のテーブルです。テーブルには、周波数、振幅、位相、および、PSD (Time-Integral Amplitude²) が表示されます。「% パワー」はすべての成分の合計が 100% になり、「相対 %」はパワーが最高の成分に 100% を割り当てます。
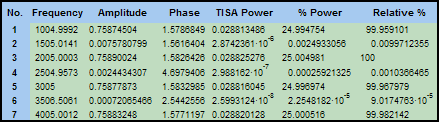
「フーリエ」は、「スペクトル」と「データ」の2つのプロットを内容とする文書です。
ここでは、データが不均等に配置されている場合に使用する FlexPro のフーリエスペクトル解析の機能について説明します。ここでは、不均一にサンプリングされたデータ用に設計されたフーリエプロシージャーに焦点を当てます。
常に均一にサンプリングされたデータで作業する場合は、このチュートリアルの残りの部分をスキップできます。
サンプル プロジェクト データベースの Tutorials フォルダーの Fourier Uneven サブフォルダーを開き、ダブルクリックして Data という 2D ダイアグラムを開きます。
これはこのシグナルのグラフです。浮動小数点値が 1000 個あります。x 値は 0 から 10 の範囲で増加していますが、等間隔ではありません。これは、不等間隔のフーリエ アルゴリズムの最悪のシナリオです。
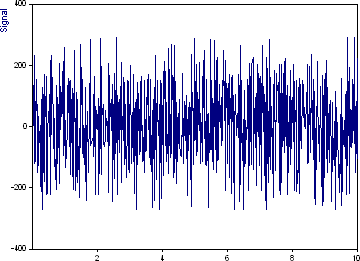
このデータ セットには、周波数 30 (振幅 100、位相 3π/2)、周波数 70 (振幅 100、位相 π)、周波数 120 (振幅 100、位相 π/2) の3つのスペクトル ピークが含まれています。平均ナイキスト周波数は 50.05 です。したがって、平均ナイキスト限界を超えるピークが2つあります。
不均一にサンプリングされたデータと均一にサンプリングされたデータとの重要な違いの 1 つは、平均ナイキスト限界を超える情報は、自動的に低い周波数にエイリアスされないことです。一部のデータはより密に間隔が空いており、はるかに高い「ローカル」なナイキスト周波数をサポートしているため、この平均ナイキスト周波数を超える情報を抽出できます。
同様に、ローカルなナイキスト周波数が全体の平均よりも小さい、間隔の広い点も存在します。したがって、平均ナイキスト範囲にある情報は不完全なものになります。
Lomb-Scargle ピリオドグラムは、データ間隔が均一でないインスタンス用のフーリエスペクトルを生成するアルゴリズムです。
ダイアグラムを閉じて、Signal データセットを選択状態にします。
挿入 [解析] > 解析ウィザードをクリックします。「スペクトル解析」内の「不均等間隔データ解析」を選択し、「不等間隔データフーリエ」を選択します。「次へ」をクリックします。
解析ウィザードのステップ 2 では、はじめに平均ナイキスト周波数と同じ最大周波数を持つウィンドウ化されていないフーリエスペクトルを調べることから始めます。
「スペクトルタイプ」には、「正規化dB」を選択します。「ウィンドウタイプ」には、「矩形 -13dB W=1」 (ウィンドウなし) を選択します。「周波数の数」を 1024 に、「ナイキスト倍数」を 1.0 に設定します。「最大ピークカウント」をチェックし、3 を入力します。ホワイトノイズの許容限界 % を 99 に設定します。
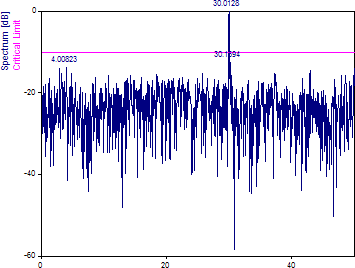
周波数 70.0 と 120.0 のピークは平均ナイキスト値を超えているため、周波数 30.0 のピークのみが見つかります。
最大のピークは 99% の許容制限を超えています。つまり、この最大のスペクトル特性がランダム ノイズによる偶然から生じた可能性は 100 分の 1 未満です。別の言い方をすると、同等の分散を持つ 100 個のホワイト ノイズ データ セットのうち、この大きさのピークを示すものは 1 つもないと予想されます。
また、このアルゴリズムでは周波数 0 値が生成されない点に注意してください。
ナイキスト倍数を 2.0 に変更します。スペクトル特性の密度を同じに保つには、周波数の数を 2048 に増やします。
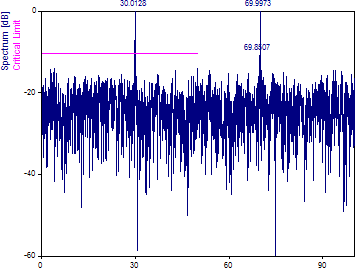
これにより、スペクトルが 30 と 70 の周波数成分が表示される点に注目してください。
ナイキスト倍数を 4.0 に変更します。スペクトル特性の密度を同じに保つには、周波数の数を 4096 に増やします。
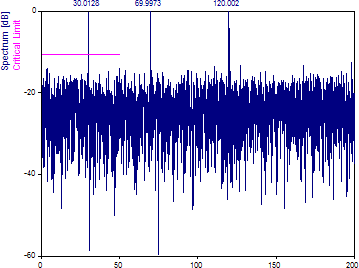
スペクトルを平均ナイキスト限界の 4 倍まで拡張すると、周波数 120 のピークを含むすべてのスペクトル成分が表示されます。
なお、このアルゴリズムでは、内挿が適用される点に注意してください。つまり誤差がない訳ではありません。データ内の正弦波はノイズなしで存在しますが、それでも約 -25 dB のノイズフロアが観測されます。高ダイナミックレンジのフーリエ解析にこのプロシージャーを使用できる範囲は、これにより制限されます。
FlexPro はアルゴリズムを拡張してウィンドウ処理機能を用意しています。この中には、不等間隔にサンプリングされた時間値に適用できるウィンドウがすべて含まれます。チェビシェフ と Slepian (DPSS) ウィンドウは使用できませんが、特定のサイドローブレベルに対して可能な限り最も鋭いスペクトルピークを作成できる特別なチェビシェフ近似ウィンドウを使用できます。
「ウィンドウタイプ」を 「Cos3 最小サイドローブ -71dB W=3」に変更します。
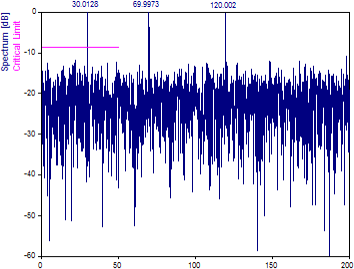
アルゴリズムの内挿誤差により、データのテーパリングではほとんど改善が見られません。
Lomb-Scargle ピリオドグラムには通常、従来型の指数分布に基づく信頼限界 (confidence limit) が含まれます。これは FlexPro では使用されません。代わりに、完全な許容限界 (Critical Limits) を利用できます。等間隔のフーリエプロシージャーと同様に、各データウィンドウには個別の許容限界モデルが使用され、これらは計算コストの高いモンテカルロ試行に基づいています。横軸の値の分布は許容限界に影響を及ぼす可能性があるため、表示される許容限界は近似値として考慮する必要があります。
ウィンドウ タイプを「矩形 -13dB W=1」に変更します。正規化に「パワー」に指定し、「ナイキスト倍数」フィールドを 3 に指定します。スペクトルタイプには「振幅」を選択します。
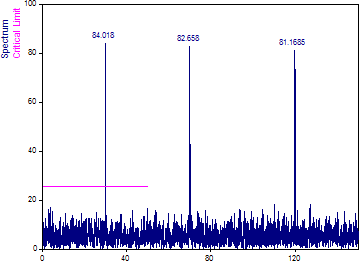
等間隔のフーリエ解析では、ウィンドウ処理を行わないと実際の振幅がスペクトルプロットに現れますが、Lomb-Scargle アルゴリズムでは、スペクトル内にシグナルのパワーを保持する必要がある場合は減衰が発生します。データウィンドウを使用すると、振幅とパワーがさらに減衰します。
この減衰は、正規化を選択することで補正されます。
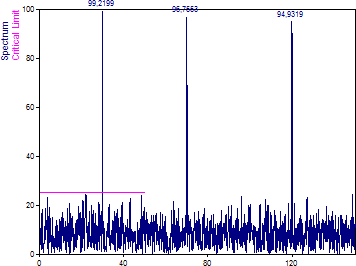
「次へ」をクリックします。ステップ 3 で、3 つのオプションすべてをチェックし、「完了」をクリックします。
FlexPro プロジェクトデータベースに、合計 8 つのオブジェクトが再度作成されます。唯一の違いは、このアルゴリズムでは位相を計算できないため、これが高調波推定オブジェクトで計算されなかったことです。
デジタルシグナル処理の優れた入門書は以下のとおりです:
FlexPro で使用される FFT アルゴリズムについては以下を参照してください:
データテーパリングウィンドウに関する情報は以下を参照してください:
マルチテーパースペクトルに関する情報は以下を参照してください: