1. 計画の評価

このチュートリアルのパート１から引き続き Design-Expert® ソフトウェア上に Longley データを開いている場合は、そのまま次に進んでください。プログラムを一旦終了している場合は、再起動して “Help” -> “Tutorial Data” から “Employment” を選択してください。

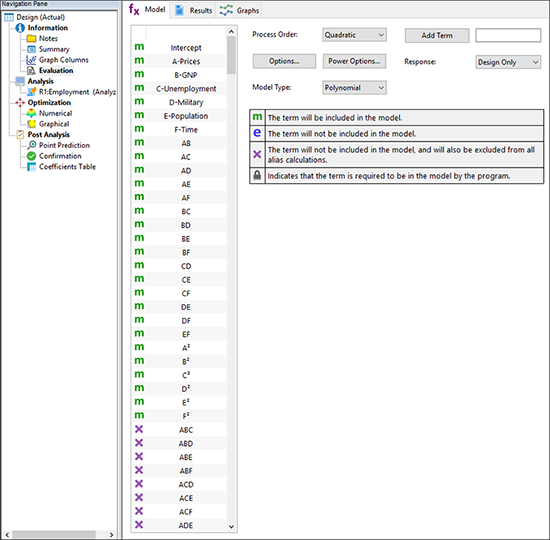
　プログラムの Design ブランチ下の “Evaluation” をクリックしましょう。ソフトウェアのデフォルトでは、2次の多項式モデルが選択されています。以下のスクリーンショットでは、Response フィールドに “Design Only” が、もう1つの応答 Employment と対になるものとして設定されています。言い換えると、応答データが存在するか否かに関わらず、因子行列の全体を評価するということです。もう1つのオプション（応答ごと）は、実験者がデータを欠損してしまった時、この “designed-for” モデルの次数を下げる場合に役立ちます。

計画の評価 (計画のみ)

 

“Results” タブをクリックして、結果を見てみましょう。

二次多項式に関する評価結果

 

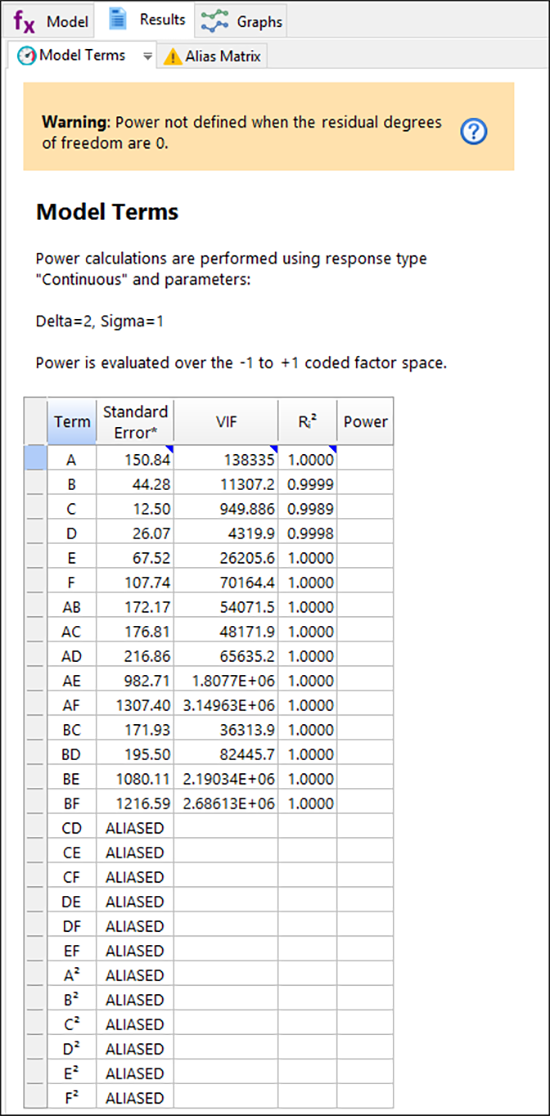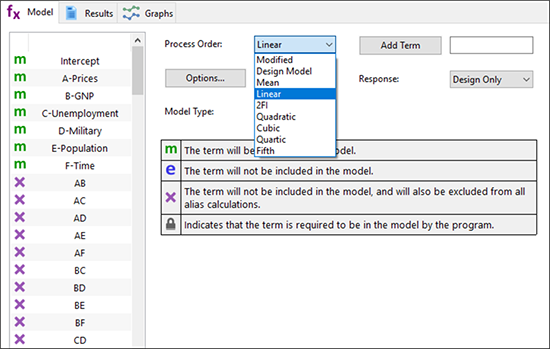
残念ながら、このモデルはエイリアスになります。例えば、効果 A は -24.5 CD などと交絡しています。“Model” に戻り、Order を “Linear” に下げてください。

OrderをLinearにリセット

 

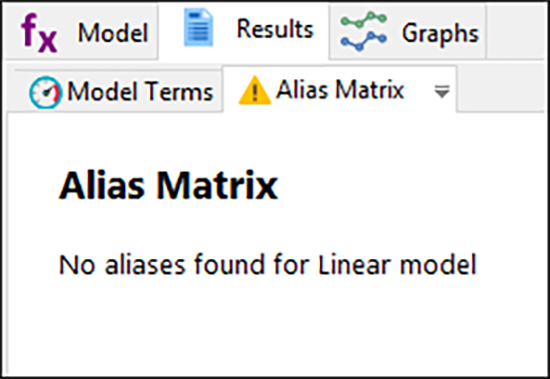
もう一度 “Results” をクリックして、“Alias Matrix” ペインに移動しましょう。“No aliases found…”（エイリアスは見つかりません）と出ました。今度の結果は良好です！

線形モデルに関する評価結果

 

これらを評価するために、“Degrees of Freedom” ペインに移動します。

Degrees of Freedom

 

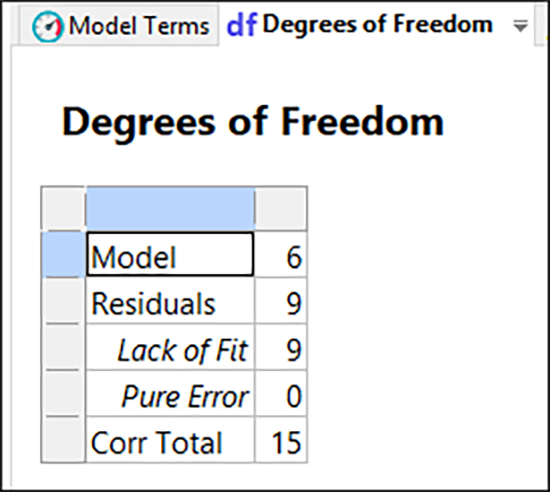ソフトウェアに表示された注釈を見てみましょう（“View” -> “Annotated Evaluation” で有効になります）。この計画は、純誤差の自由度 DF において推奨される値に届いていない点に注目してください。もちろん、これは実際には計画された実験ではなく、偶然に収集されたヒストリカルデータです。

自由度に関する注釈

 

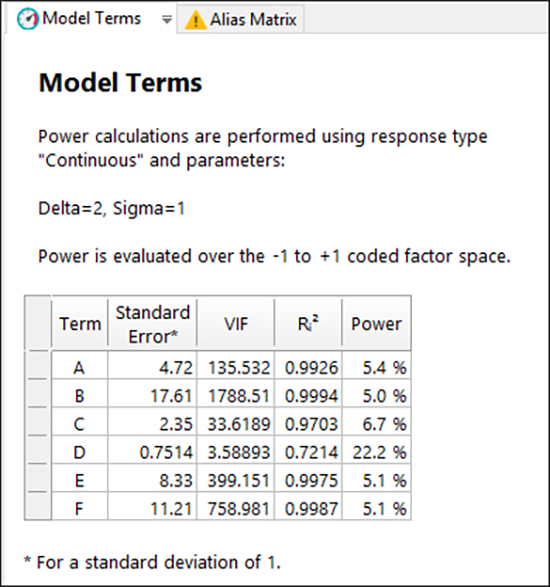
Design-Expert で評価された Model Terms セクションを調べてみましょう。検定の結果、適正な計画であると判断された統計値があるでしょうか？一切ありません！

検出力（Power）を含むモデル項に関する詳細な検定結果

 

次に、Leverage に関するレポートを見てみましょう。これらの統計結果は驚くほど良好です。平均の２倍を超えるものはありません。

　上記以外の統計についても評価することができます。“Model” に戻り、“Options” をクリックして、Matrix Measure と Highlight Correlation Values のチェックマークを（まだ選択していない場合は）オンにしてください。

レポートに表示させる追加オプションのチェックを有効にする

 

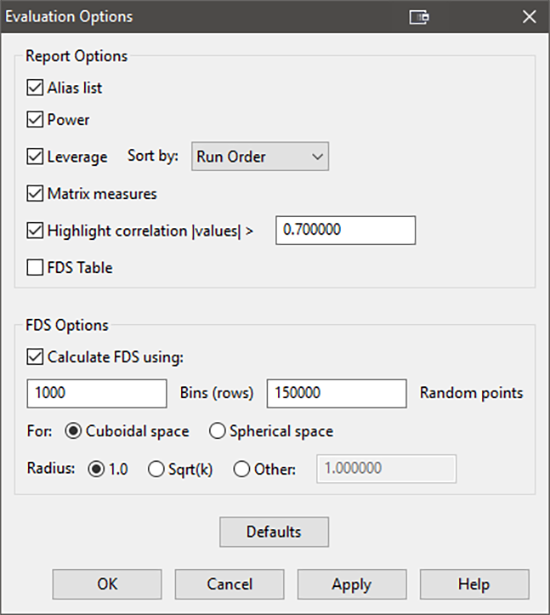“OK” および、“Results” ボタンをクリックしてこの結果を見てみましょう。次に、Matrix ペインを確認し “Matrix Measures” タブに移動して、新たに追加された統計結果を確認することができます。

計画を評価するための行列評価

 

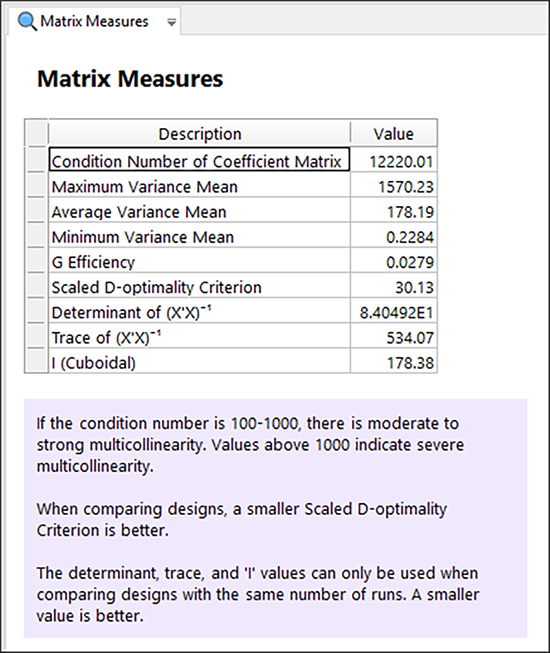ここで示された条件数（12,220）は、計画行列において重度な多重共線性を表すと見なされる水準（1,000 以下）を、大きく上回っている点に注意してください。“Correlation Matrix” ペインと “Pearson’s r” ペインをチェックして、特定の相関を確認することで、その理由が分かります。

※注意：ツールバーの青いレイアウトアイコンをクリックして、様々なペインレイアウトを選択してみてください。また、各ペインのタブをクリックし、様々なセクションにドラッグして、画面を使いやすいようにカスタマイズしてください。

 

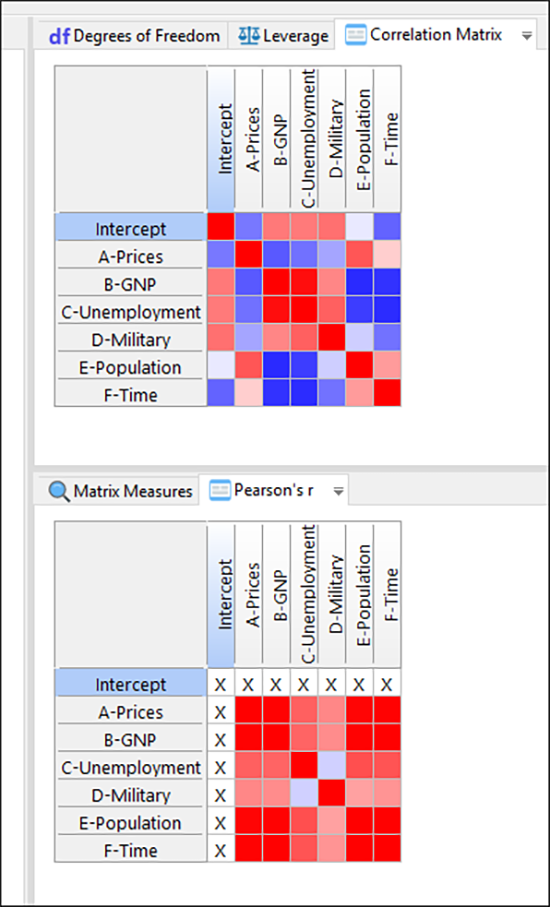
Correlation Matrix では、-1 (完全負相関) から +1 (完全正相関) の範囲で、因子がどのように互いに相関しているのかを示します。これらの相関はグリッド形式で色分けされ、問題のありそうな箇所が一目でわかるように表示されます。ここで、因子を相関させたくないことを忘れないでください。望んでいるのは、それらが応答にどのような影響を与えるかについて独自の推定を得ることです。そのため、グリッド内の白の四角は問題ありません。このグリッドをざっと見るだけで、因子間（濃い青色と赤）に多くの相関が存在していることが分かります。Longley 氏が回帰ソフトウェアで検定するために、このデータセットを選択したのは当然といえます。ピアソンの ｒ 行列グリッドでは、ピアソンの相関係数が表示されています。これは相関の計算方法が異なるだけです。チップス（）アイコンをクリックすると、詳細を確認することができます。

相関行列

 

それでは参考までに、“Graphs” タブをクリックして、ツールバーから “Perturbation” を選択してください。

標準誤差の摂動プロット

 

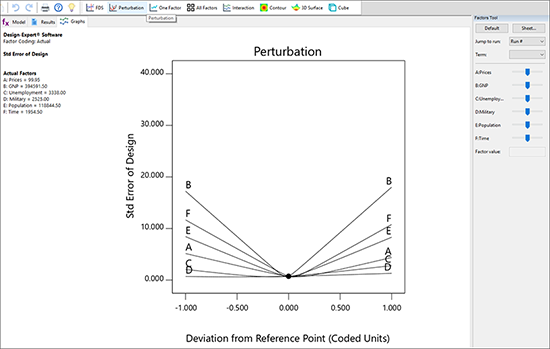因子 B と F が、標準誤差の最も極端な軌跡を示している点に注目してください。続いて、Graphs Toolbar で “3D Surface” を選択してみましょう。Factors Tool にある F:Time を右クリックして、それを “X1 axis” に変更してください。

因子 B と F の標準誤差の 3D 表示

 

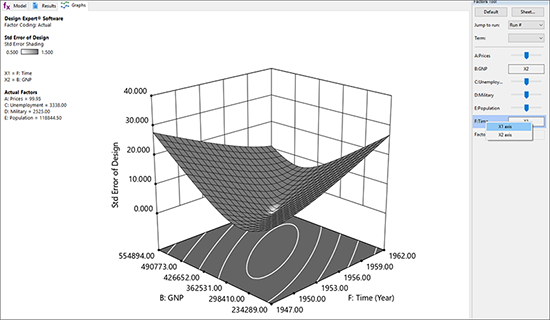これ以上分析しても意味はありません。この「計画」は、適正な実験を判断する全ての検定で、不合格と判定されるのはもはや明らかです。これこそ正に、偶発的状況に置かれたデータが、一般的に抱える非合理性なのです。