Mathematica による SVD ― Singular Value Decomposition [特異値分解]―

1. はじめに

データサイエンスの分野で扱うデータの次元は膨大であり、全ての次元のデータを取扱うにはメモリ、CPU などのハードウェア、計算速度の観点から様々な困難がともないます。そのため、意味のある次元のデータだけを抽出しデータ容量を小さくする必要性が生じます。このようなデータの次元削減に使用される手法の一つに SVD (Singular Value Decomposition [特異値分解]) があります。本記事では、SVD を利用したデータの次元削減の方法について、画像圧縮の実例を含めてご紹介します。

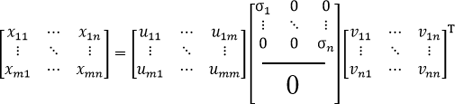
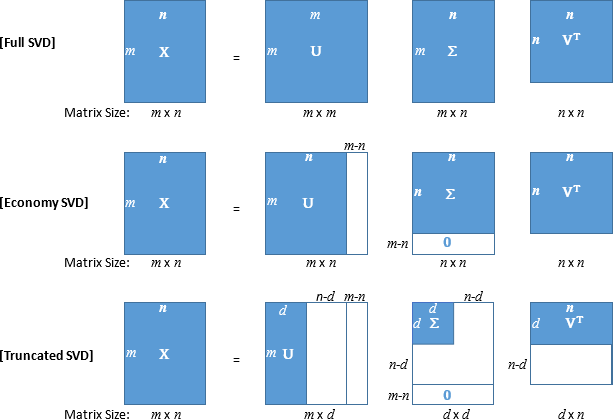
2. SVD (Singular Value Decomposition [特異値分解]) とは

　SVD (Singular Value Decomposition [特異値分解]) はデータサイエンスの分野で基本となる計算手法の一つであり、データの次元削減、つまりデータを圧縮するための手法の一つとなります。ここでは SVD によりデータがどのように分解されるかについて簡単に説明します。例えば、画像などの m × n の行列データ X があるとします。SVD を計算すると次の U、Σ、V の三つの行列に分解することができます。U は m × m の左特異行列、Σ は m × n の特異値行列、V は n × n の右特異行列です。本記事では、m ＞n とします。

[Full SVD]

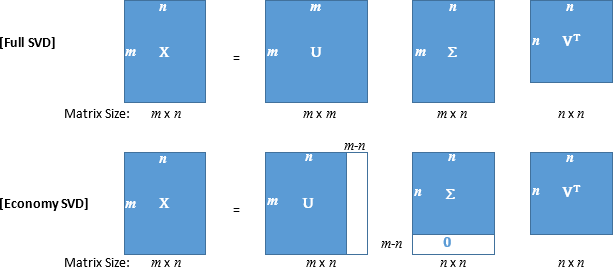
特異値行列の σ は対角行列で σ1 ≧ σ2 ≧ … ≧ σn の関係があります。また、特異値行列は n +1 行以降の成分が ０ となるため、U、Σ の m × n の成分の内、赤枠の部分は省くことができます。上式が Full SVD と呼ばれるのに対し、下式は Economy SVD と呼ばれています。

[Economy SVD]

Economy SVD をさらに展開すると次のようになります。

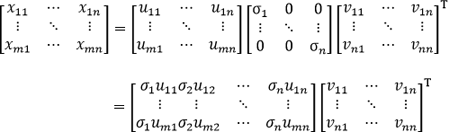
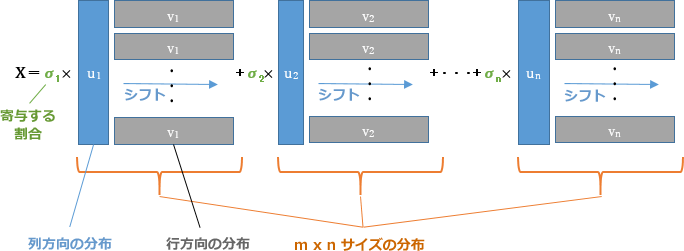
上式は直積であるため更に式を展開すると次のような二項積に σn を掛けたものの総和として表すことができます。

ここで、U、VT を次のように、それぞれ n 列、n 行の成分からなる行列と考えると、

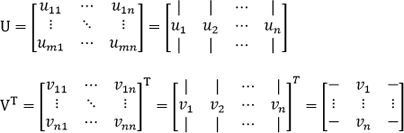
下記のように簡略化して表すことができます。

上式の意味としては、uiviT に関しては列方向の分布である un をシフトさせながら、行方向の分布である vn と掛け合わせることにより、m × n のサイズの領域での un の分布を算出していると考えることができます。また、uiviT に σn を乗ずることから、σn は uiviT が X というデータにどれだけ寄与しているかを表していると考えることができます。

3. SVD による画像データの圧縮

実際に画像データを使用し、SVD によりデータを圧縮 (次元削減) できることをご紹介します。使用する画像データは Mathematica の戦闘機の画像サンプルデータで次のようにして呼び出します。

読み込んだ後の処理は次のようになります。

  1. 読み込んだデータのサイズが 512×512 であるため、512×500 の縦長の行列にします。
  2. SingularValueDecomposition で SVD を行います。MatrixRank[xx] は Economy SVD を計算するためのもので、行列 xx のランクです。このように一つのコマンドで SVD の計算を簡単に行うことができます。
  3. ListPlot で特異値行列の対角成分をプロットします。
  4. Accumulate で対角成分の累積値を計算し、％ で表示させます。
  5. Nearest で累積値が 80％になるインデクスを割り出します。
  6. Show で二つの ListPlot で対角成分の累積値と累積値 80%になる箇所をプロットします。

このようにして得られた結果が次の図になります。左側の図が特異値行列の対角成分 σ をプロットしたもので、右側の図が対角成分の累積分布です。両図ともに横軸は特異値行列のランクとなります。左側の図からは σ の値が急激に減衰していく様子がわかります。また、右側の累積分布からはランク 52 で累積値が 80％ に達していることがわかります。

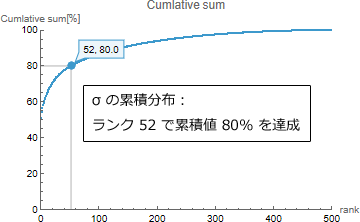つまり、下記の式で、d=52 となることから、データ数 512×52=26624 個の U、データ数 52×52=2704 個の σ、データ数 52×500=26000 個の V の計 55328 個のデータ数で X の 80％ までを近似できることを意味します。X のサイズが 512×500=256000 であることから約 20％ までデータ数を圧縮することができます。

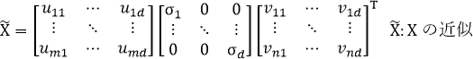
このように、σ の累計を基に近似する SVD を Truncated SVD と呼びます。

実際に d=52 として SVD を計算し、画像を再構築すると次のようになります。

  1. SingularValueDecomposition で SVD を行います。UpTo[52] でランク 52 まで SVD を行います。
  2. 特異値行列の次元を確認します。
  3. 元イメージを表示させます。
  4. 圧縮し次元削減したイメージを表示させます。

左側が元イメージ、右側が圧縮し次元削減したイメージです。データを約 20％ まで減らしても、ほぼ再現ができていることがわかります。

元イメージ 圧縮して次元削減し、再構築したイメージ

4. おわりに

本記事では Mathematica で比較的短いスクリプトで SVD による次元削減を行えることをご紹介しました。今後はさらに応用例をご紹介していきたいと思います。