この時期になるとスタジオ地図・細田守監督作品『サマーウォーズ』(2009) がよく話題に上ります。今年も8月1日に「金曜ロードショー」で放送されました。 劇中では主人公が暗号を解読するシーンが登場しており、この暗号が何の暗号なのかは触れられていませんが、「RSA 暗号」が有力ではないかとされています。
今回はこの RSA 暗号を Mathematica を使って実装し、実際に暗号を解読するところまで試してみたいと思います。
RSA 暗号については以下の通りです。
RSA 暗号(RSAあんごう)とは、桁数が大きい合成数の素因数分解が現実的な時間内で困難であると信じられていることを安全性の根拠とした公開鍵暗号の一つである。暗号とデジタル署名を実現できる方式として最初に公開されたものである。
(引用元:Wikipedia https://ja.wikipedia.org/wiki/RSA%E6%9A%97%E5%8F%B7 )
具体的には次のような手順で暗号化と復号を行います。
平文 m を暗号化: c ≡ me mod n
暗号文 c を復号: m ≡ cd mod n
まずは鍵の生成を行います。
安全性を保つには p, q に大きな素数を選ばなければなりませんが、ここでは動きを見るために小さな素数を選択します。
![]()
素数であることを確かめるには PrimeQ を利用できます。
![]()
また Prime を使って n 番目の素数を求めることもできます。
![]()
続いて n と φ を求めます。
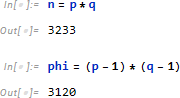
次に e を選びます。よく使われる値は 3 と 65537 のようですが、今回はこれらの値は使わずに 17 と設定しておきます。
![]()
e と φ が互いに素であることは GCD を使って確認できます。
![]()
最後に d を求めます。Mathematica では PowerMod もしくは ModularInverse を使うことで求めることが可能です。
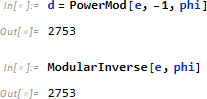
これで公開鍵 n = 3233, e = 17 と秘密鍵 d = 2753 の準備ができました。これを使って暗号化と復号を試します。
公開鍵を使って 1 から 10 の値のリストを暗号化してみます。

1 は変わっていませんが、それ以外の値は大きく変わったことが確認できます。
暗号化した数値のリストを秘密鍵を使って復号してみます。
![]()
正しく復号できることが確認できました。
なお、今回は p, q に小さな素数を使いましたので、FactorInteger を使って公開鍵 n からこの値をすぐに求めることが可能であり、安全性はありません。
![]()
上の例では数値のリストを暗号化しましたが、一般的には文字列を暗号化したい場合が多いと思います。
ToCharacterCode を使うことで文字列を数値 (文字コード) のリストに変換できます。
![]()
この数値に対して暗号化と復号を試してみます。

文字コードから文字列の変換には FromCharacterCode が使えます。
![]()
こちらも正しく復号できることが確認できました。
最近の鍵は 2048 bit 以上、桁数にすると600桁を超える値が使われているそうです。
試しにどれくらいの長さだと素因数を求める難しくなってくるのか簡単なテストを行ってみました。
Prime を使って a 番目の素数 と a + 1 番目の素数を求め、その二つの数を使って n を計算し、その結果を FactorInteger に渡して素数を求める関数を定義して実行してみます。

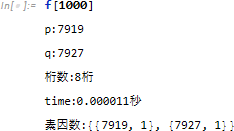
まず、a を 3000 とすると、7912、3001番目の素数は 7927 となり、n は 8 桁の数となることが確認できます。なお、桁数は IntegerLength を使うことで確認できます。そして FactorInteger でその素因数を求めてみると、ほぼ 0 秒で計算できていることが分かります。
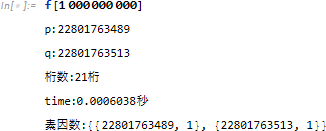
次に a = 1,000,000,000 とすると、桁数は 21 桁になりますが、こちらもすぐに結果が返されることが確認できます。
さらに a の桁数を増やして a = 100,000,000,000,000,000 とすると、実行に少し時間がかかるようになります。
しかし、素因数を求める箇所は 0.05 秒程しかかかかっていませんので、素因数ではなく素数を求めるところに時間がかかっているようです。
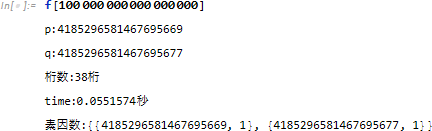
さらに a の桁数を1つ増やしたところ、Prime 関数が値を返さなくなりました。
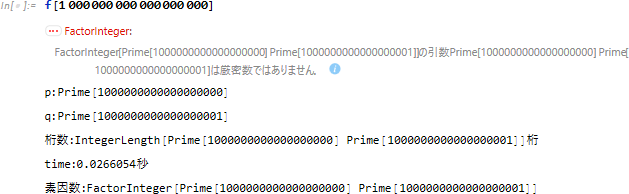
Prime について少し試してしてみたところ、Prime では 21京6300兆番目を超える素数は求められないようです。
![]()
確認できた素数を用いて計算を実行してみると、秘密鍵の桁数は 38 桁で、素因数を求める時間は 0.066 秒でした。この桁数でもすぐに求められ、まだ安全性は無いようです。
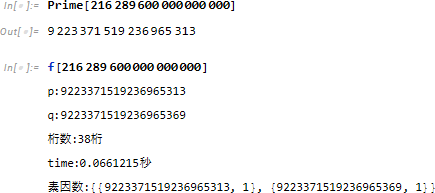
このテストでは素因数分解がどの程度の桁数から難しくなるのかを確認する前に、素数を求めるところで躓くという結果になりました。
ここまで RSA 暗号を定義に沿って実装してみましたが、Mathematica には組込みの関数も用意されています。
まず秘密鍵と公開鍵を生成するための関数に GenerateAsymmetricKeyPair があります。
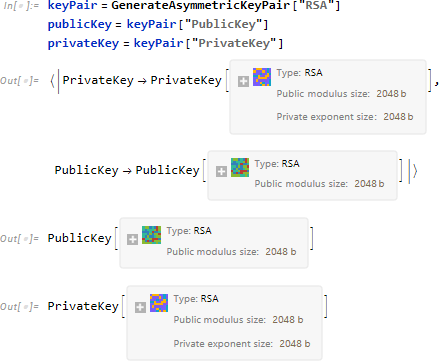
暗号化には Encrypt が使えます。
なお、Encrypt は入力として数値のリストだけでなくメモリ効率の良いバイト配列を使用することができます。 そのため、文字列を数値に変換する際には StringToByteArray が役に立ちます。
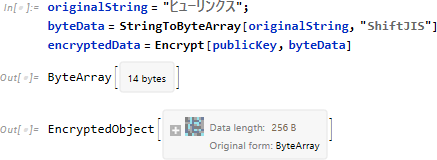
バイト配列に含まれる値を確認するには Normal が利用できます。
![]()
そして復号には Decrypt が、バイト配列から文字列に変換するには ByteArrayToString が使えます。
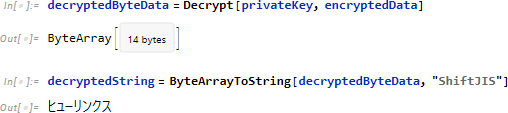
なお、生成された公開鍵の値は "PublicHexString" と指定することで確認が可能です。

これを FromDigits を使って 10進数に変換してみると、600桁を超えていることが確認できます。
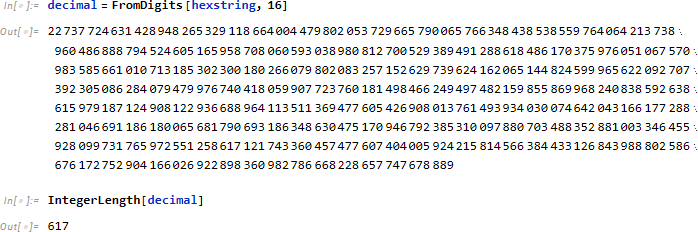
この値から素因数を求めてみようと思いましたが、確認できた範囲では結果は返されませんでした。(もしすぐに結果が返ってきたら、それはそれで問題ですが。)
評価メニュー > 評価を放棄 を選択すると、計算を中断できます。
![]()
今回は RSA 暗号の実装方法と、組込み関数を使って実行する方法を見てきました。
次回『サマーウォーズ』が放送されるときに意識してみると、印象が少し違って見えてくるかもしれません。