Mathematicaは 173 もの確率分布関数をカバーしています。これは一般的な数学の本で言及される確率分布のほぼすべてとなっています。今回はその一部を紹介し、分布から事象確率を推定する問題に取り組んでみたいと思います。
データが与えられたとき

データ分布を満足する確率分布 (この例の場合は正規分布) が見つかると
![]()
これを使い、たとえば事象 x が 1 と 2 の間に起きる確率を推定します。
![]()
(備考:![]() の記号は
の記号は ![]() dist
dist ![]() で入力します。また、
で入力します。また、x ![]()
dist は Distributed[x, dist] で置き換えることができます。)
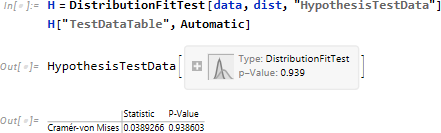
先に進む前に、この例について少し解説を追加します。データ data は一般に観測値等が使われますが、ここでは平均 2.0、標準偏差 1.0 となる正規分布 NormalDistribution からランダムに 500個選んでいます(試行回数=500)。 FindDistribution は与えらたデータを満足する確率分布を推定します。得られた分布パラメータ、今の場合、平均および標準偏差について確認してください。
推定に対し、一般的には適合度を検定します。確率分布に関しては DistributionFitTest を使います。検定関数として CramerVonMisesTest を使い、(5%棄却の) p-値から、分布が「正規分布でない」仮説は棄却されます。つまり「分布は95%の信頼度で正規分布である」ことがわかります。
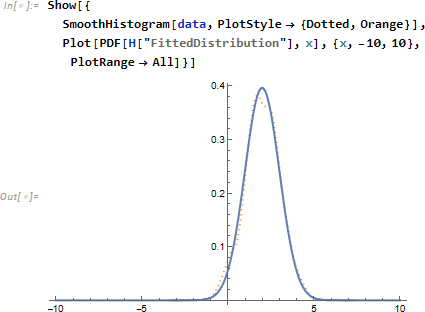
確率分布を PDF (後述) によって確率密度関数化し、視覚的に確認します。
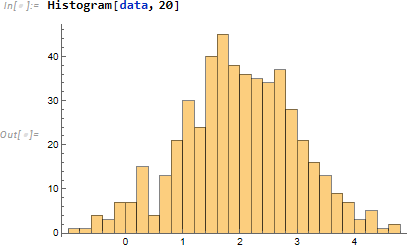
ここであらためて話を振り返ります。データが与えられたとき、まずデータの分布傾向を Histogram を使い、直観的に確認します。
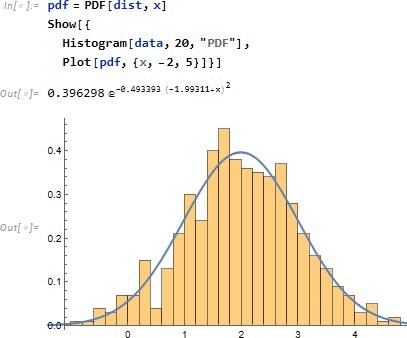
次に分布から PDF (Probability Density Function) を使い、確率密度関数 pdf を求め、ヒストグラムと重ね、両者が重なることを確認します。なお、Histogram の引数 "PDF" はヒストグラムの面積が 1. となるよう正規化します。
ついで、事象、 たとえば「 x が 1以上、2以下となる」が発生する確率を求めます。
![]()
確率は面積 (以下の薄青色部分) に対応し、
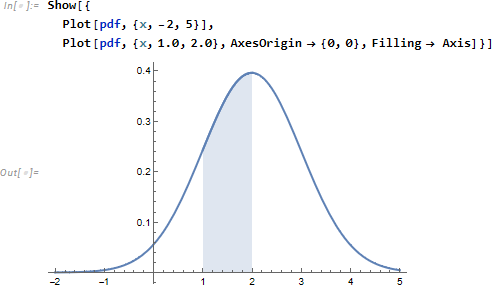
実際に積分によって面積を計算すると、確率値に一致することがわかります。
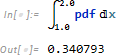
事象範囲を全領域 -∞ から +∞ にすると面積 1. 、つまり全事象の起こる確率 1. に合致します。なお、第2項は誤差です。
さらに PDF のように点推定を前提とした関数に対し、確率の累積を前提とした CDF (Cumulative Distribution Function)
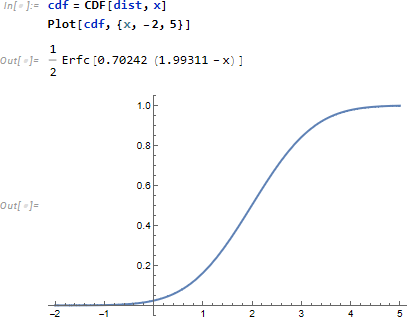
を使い、指定した事象(t=4.)までの確率累積を計算します。
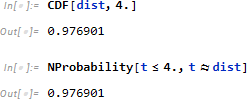
たとえば故障が累積する現場において故障率を CDF によって累積した場合、1 - CDF によって生存数を予測できます。
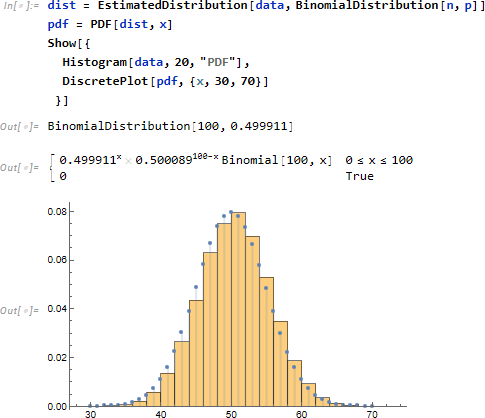
100 回の試行で 1/2 の確率で表が出る二項分布 を想定し、10万回試行した結果を data とします。

ヒストグラムを使い、大まかな分布状態を把握します。
(無限に試行した結果の)期待値は 100/2 の 50 です。
![]()
分布パラメータ n と p を類推し、結果の分布 dist から確率密度関数 pdf を求め、ヒストグラムと重ねる。なお二項分布は離散分布なので、単なる Plot ではなく DiscretePlot を使います。
[例]確率を時間(ここでは秒単位)のパラメータ(Exp[-λ t])で与えられる例を考えます。3重化された機械があり、少なくとも1台が稼働する( x ≥ 1 )確率を次のように定義します。
![]()
仮にパラメータ係数 λ を 10-8 とすると確率 p は次のように減衰します。なお視覚的には1年経過して 98%程度の確率で動作し続けることが見て取れますが(3600*24*365 は秒換算で1年を表す)、
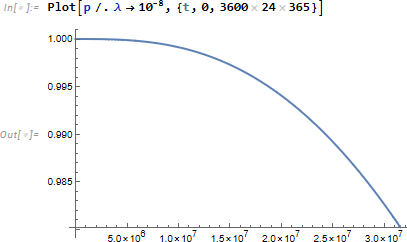
たとえば 99% 未満の確率で動作する年数を理論的に求めてみます。ここで Reduce は不等式 1-(1-ⅇ-tλ)3 ≤ 0.99 を満たす t に関する不等式を返します。結果から、動作年数は約 0.77 年と分かります。
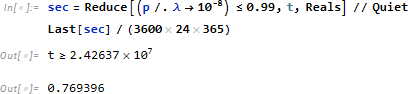
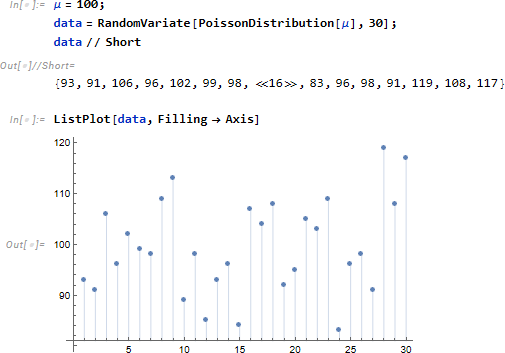
平均 μ で発生する事象はポアソン分布で表せます。ある都市の一日あたりの平均事故件数を μ = 100 とした場合、1ヶ月のシミュレーションデータ data を求めます。
この分布を使い、たとえば、1日90件以上、事故が起きる確率 p を計算します。
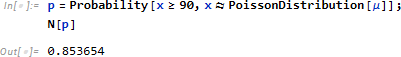
[例]書籍の誤植はポアソン分布にしたがうと仮定します。いま 384 ページの本に 158 箇所の誤植があったとし、これを平均とみなし 、以下の等式によって λ を求めます。
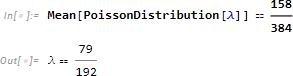
NSolve によって等式から方程式の解 λ → を計算し、
![]()
ページ p あたりの誤植分布 pageErrorDistribution を次のように定義します。
![]()
これを使い、様々な確率を計算してみます。最初は、各ページの誤植が厳密に 0 となる確率です。
![]()
これは次式と等価です。
![]()
1ページあたりの誤植が2箇所未満となる確率
![]()
は CDF を使うことで計算することもできます。
![]()
最後に1ページあたりの誤植が1箇所以上ある確率を計算してみます。一般的には SurvivalFunction を使いますが
![]()
Probability を使い、次のように求めることもできます。
![]()
物体の強度を統計的に記述するための確率分布の1つ。特に時間に関する劣化現象や寿命について統計値を与えます。サンプルデータとして形状パラメータ α = 2、尺度パラメータ β =1000 (時間) を仮定します。試行回数は 1000 とします。
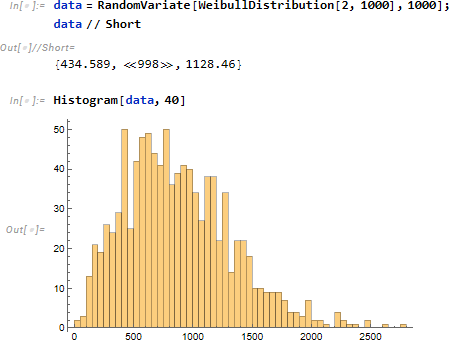
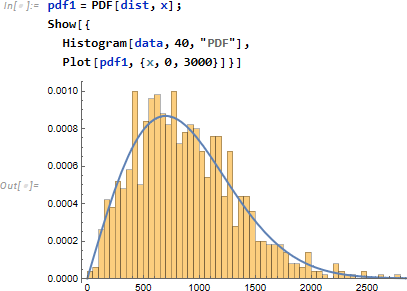
データ data から分布を推定します。予想とは違った分布 Rayleigh が返ってきましたが、
![]()
このデータ例には当てはまりそうです。
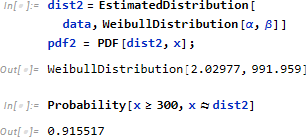
ついで300時間以上、故障しない確率を求めます。
![]()
本来のモデル Weibull 分布 をモデルとして指定し、EstimatedDistribution でパラメータ α, β を推定し、確率を計算します。
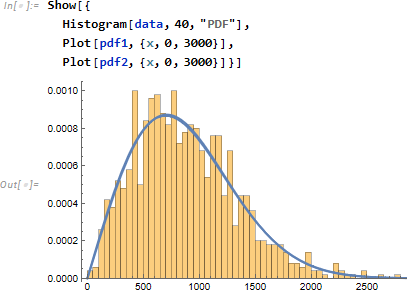
有限の試行回数内では、複数の分布が1つの確率密度関数に重なることがあります。
英単語の語長データ data
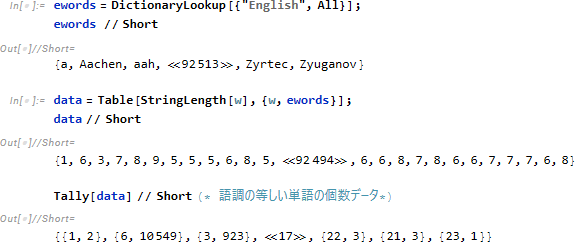
に対し、二項分布 dist を想定し
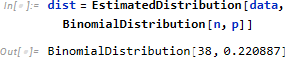
データヒストグラムと確率密度関数を重ねて確かに二項分布になっていることを確認します。
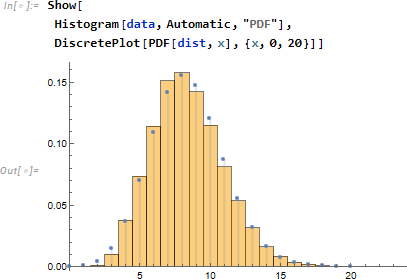
イタリア語でも試してみましょう。
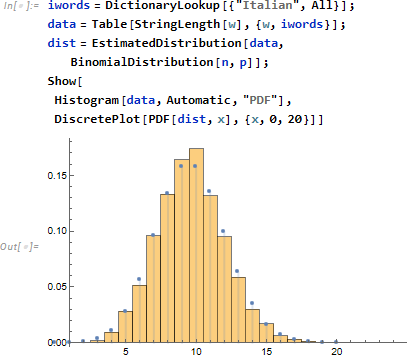
テキストが与えらたとき、言語によらず単語の出現頻度に関し、同一の分布となることを示します。ここではテキストとして「世界人権宣言」(英語版)を例にとり、Tally によって単語出現頻度を求め、頻度のみを data とします。
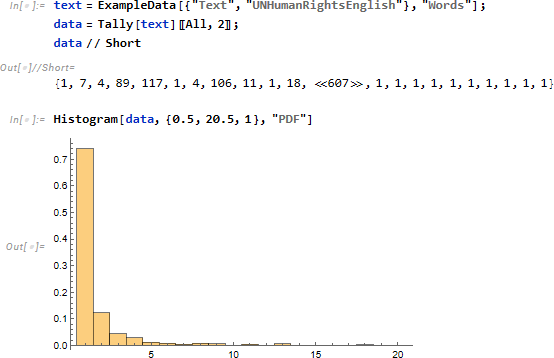
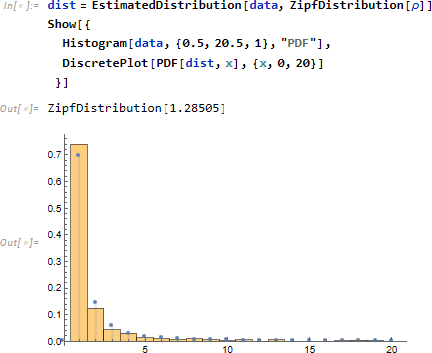
Zipf 分布を仮定し、EstimatedDistribution によって分布パラメータ ρ を推定し、結果 dist を PDF 化し、上記ヒストグラムと重なることを確認します。
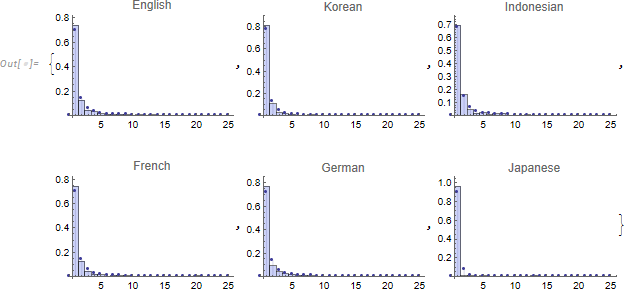
単語の語長と異なり、出現頻度に関して Zipf 法則は様々な言語に当てはまります。なお、言語以外の分野において Zipf 法則が成り立つ様々な例が知られています:Zipf's Law 。
次回は「関係を予測する」という観点からグラフ理論を概説する予定です。