この記事を Notebook で開く先日ヒルベルト変換についてのお問い合わせをいただいたため、Mathematica で実行するにはどうすれば良いかを調べてみました。
本記事では Mathematica を使って
を求めてみます。
なお、計算方法については小野測器様で公開されている資料 (https://www.onosokki.co.jp/HP-WK/eMM_back/emm180.pdf)を参考にしました。
今回は実信号 x[t] をチャープ信号とし、次のように定義します。
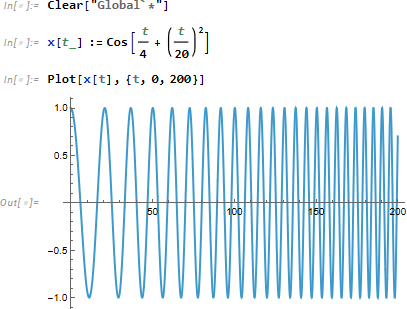
x[t] のヒルベルト変換 
は
*は畳み込み、積分はコーシーの主値積分
によって定義されるため、Convolve を使って畳み込みを求めてみます。
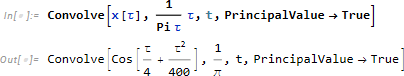
残念ながらこの信号では求めることができませんでした。(他の信号ではこのまま求められるものもありました。) そこで、今度はフーリエ変換を行ってから位相をずらし、逆フーリエ変換を行う方法を試してみます。 まず、X[t] を求めます。
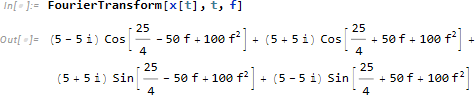
続いて、
を求めます。
(% は一つ前に実行した結果です。計算の順序によっては同じ結果が得られないため注意が必要です。必要であれば任意の変数に代入してください。)
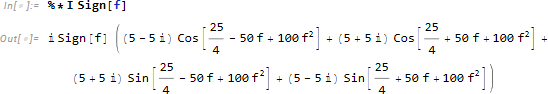
そして、逆フーリエ変換により を求めます。(この信号では実行に少し時間がかかります。)
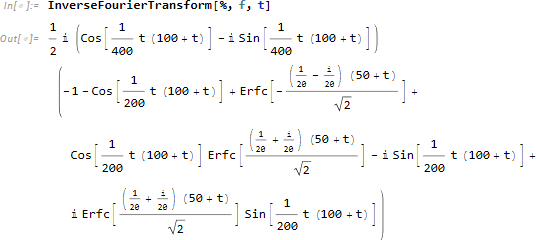
無事に が求まりました。
式が少し長いため、FullSimplify を使って簡略化を試します。
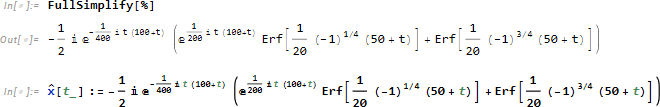
求まった関数をプロットしてみます。
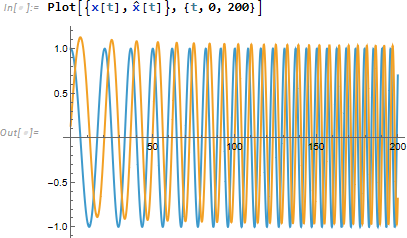
を求めることができましたので、解析信号 z[t] を求めます。
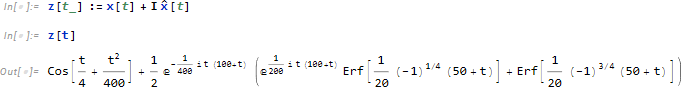
包絡線は z[t] の絶対値として求められるため、Abs を使用します。
関数をプロットしてみます。
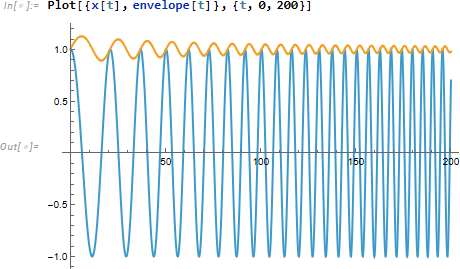
式の形を確認してみます。
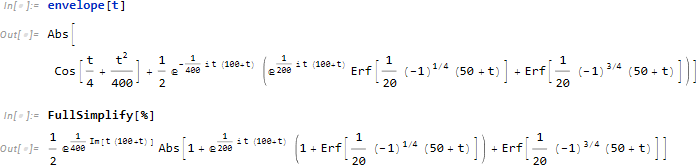
t が実数であると仮定すると、もう少しシンプルな形になります。
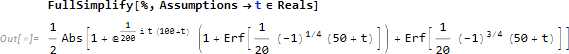
瞬時位相 θ[t] は
の式で求められるため、ArcTan を使って求めます。
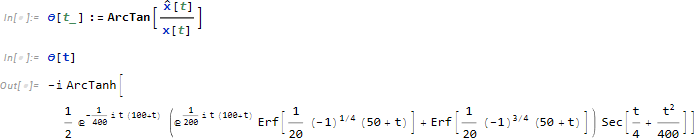
関数をプロットします。
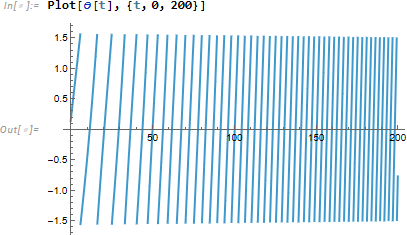
なお、ArcTan を使わずに、Arg を使って z[t]の偏角を求める方法もあります。
ArcTan は -π / 2 から π / 2 の値を返しますが、Arg は -π から π の値を返します。
ただし、こちらの方法では式に Arg が残ってしまいます。
Arg は微分ができないため、次の瞬時周波数を求めることができません。
瞬時周波数 f [t] は
の式によって求められるため、D を使って求めます。
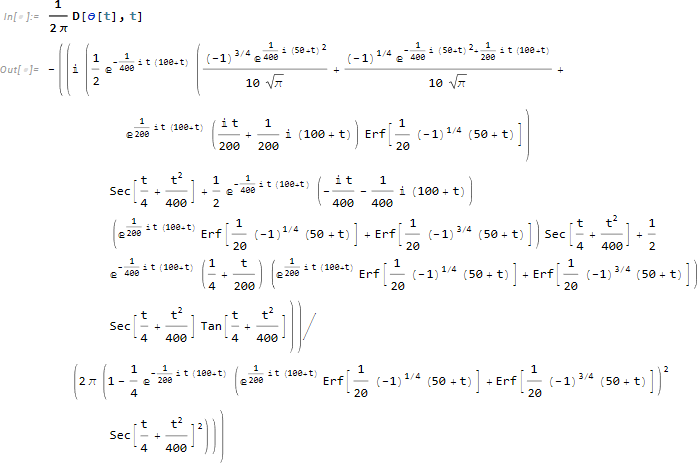
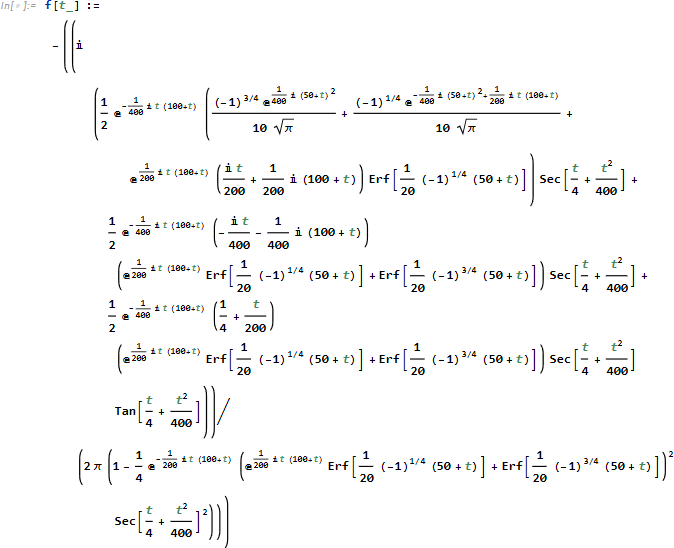
求まった関数をプロットします。
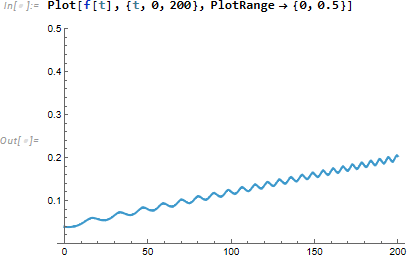
今回はヒルベルト変換を使って実信号を複素時間信号に変換し、包絡線や瞬時周波数を求めてみました。
他のソフトでは、数値データに対してヒルベルト変換を行う例は見つかりましたが、数式に対してヒルベルト変換を行う例は見当たらなかったため、この辺りは Mathematica の強みではないかと思います。
なお、いくつかの信号を試してみましたが、信号によっては途中式がかなり長くなってしまい、計算にかかる時間も長くなるケースがありました。
そのため、場合によっては FullSimplify を使って途中で出力される式を簡約化するなどの工夫が必要になるかもしれません。
