Mathematica でグレブナー基底を使って連立方程式を解いてみる

はじめに

普段 Mathematica で連立方程式を解きたい場合には Solve や NSolve などの関数を使いますが、先日グレブナー基底を使うことでも連立方程式を解くことができることを知りました。そこで今回はグレブナー基底を使って実際に連立方程式を解いてみたいと思います。

Mathematica でグレブナー基底を求める

グレブナー基底がどのようなものか、また、グレブナー基底を使って連立方程式を解く方法の詳細については、知らない人向けに分かりやすく説明しているブログなどをウェブ上で簡単に見つけることができるためここでは省略しますが、グレブナー基底の発想の原点は「多項式同士の除算計算」の一意性にあり、連立多項式を解く際に解が存在するとしたらグレブナー基底は解に至る手順に一意性を保証するそうです。

Mathematica でグレブナー基底を求めるには GroebnerBasis 関数を使用します。

２元１次連立方程式

まずは下記の簡単な２元１次連立方程式を解いてみたいと思います。

この方程式の解は x=1, y=2 です。

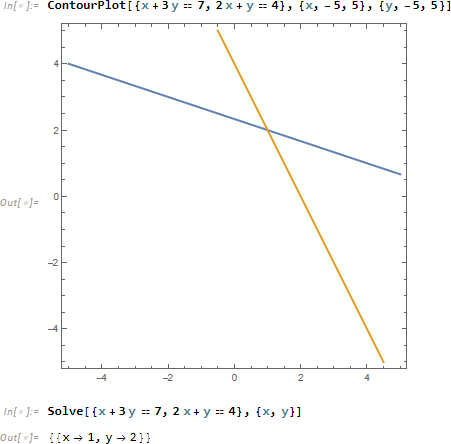
グレブナー基底を求めるために、まずは右辺の値を左辺に移行することにより連立方程式から多項式を求めます。

そして、この多項式を GroebnerBasis 関数に入力して実行します。GroebnerBasis 関数の１つ目の引数は多項式のリスト、２つ目の引数は変数のリストです。

なお、多項式の形にすることは必須ではないようで、連立方程式の形のまま入力しても実行できました。

今回は１次の方程式のため、得られた結果からすぐに y=2, x=1 ということが分かりますが、求まったグレブナー基底に ==0 を付けて、これらの解が求められることを確かめてみます。

２元２次連立方程式

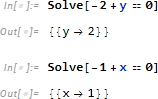
続いて２元２次連立方程式についても同様にグレブナー基底を使って解いてみたいと思います。

この連立方程式の解は４つあります。

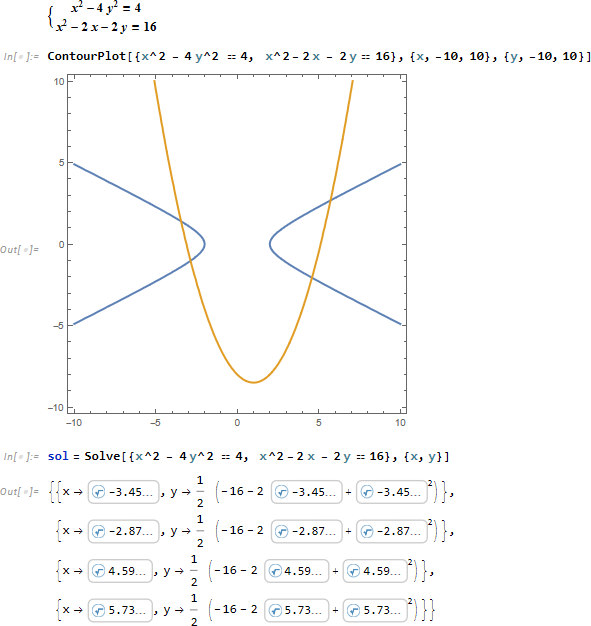
結果は Root の形で返されるため少し分かりづらいです。 おおよその値が知りたい場合には N 関数を使います。

それでは、先ほどと同様に多項式の形にしてからグレブナー基底を求めます。

この連立方程式では２つの基底が求まります。

少し話が脱線しますが、求まったグレブナー基底を ==0 と置いてプロットしてみると、グラフの形はかなり違いますが、解の位置は変わっていないように見えることが分かります。

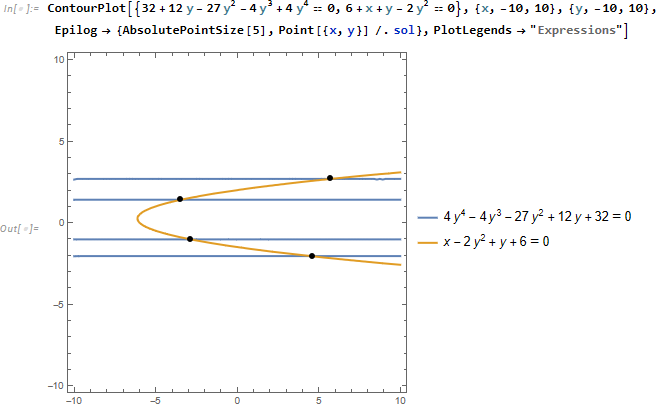
さらに元の方程式と重ねて表示させてみます。

下の例では元の２つの方程式を赤とマゼンタ、求まった２つの基底を青とシアンで描画します。

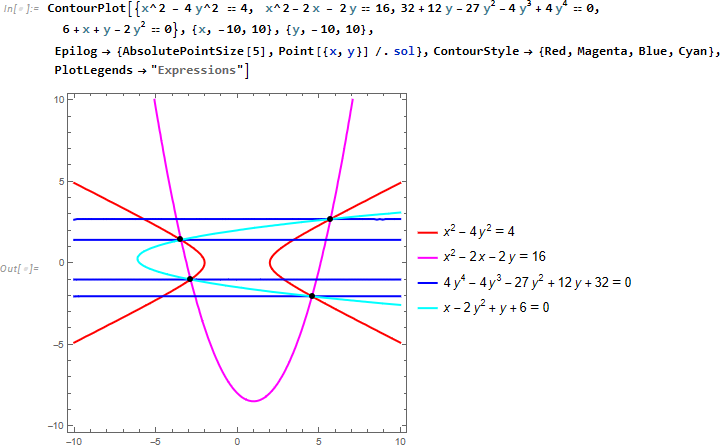
本題に戻り、先ほどと同様に求まったグレブナー基底から方程式の解を求めてみます。

求まった１つ目の基底は y のみに関する４次の多項式のため、この式を ==0 と置いた方程式を解くことで y を求めることができます。

４つの解が求まりましたが Solve の結果と一致する結果が無いように見えます。

しかし、FullSimplify を使って Solve の結果を簡約化すると、順序は異なりますが同じ結果が得られていることを確認できます。

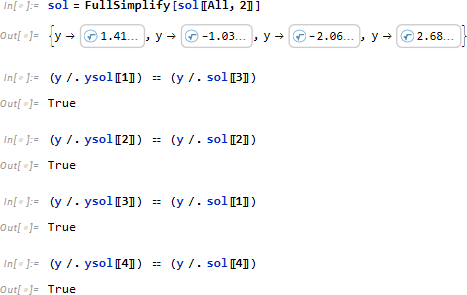
求まった２つ目の基底は x と y に関する式のため、この式を ==0 と置いた方程式に求まった y を代入してから方程式を解くことで、対応する x の値が求められます。試しに得られた１つ目の y を代入してみます。

こちらも最初の Solve で得られた解と一致するものが無いように見えますが、FullSimplify を使って簡約化すると同じ解が得られます。

同様に他の y に対応する x の値を求めてみます。

得られた結果をまとめます。

おわりに

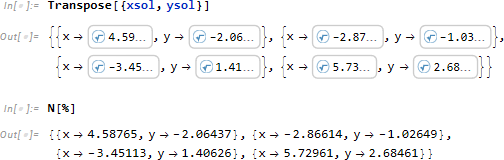
今回は Mathematica でグレブナー基底を使って連立方程式の解を求めてみました。もちろん最初から Solve を使って直接連立方程式の解を求める方が簡単なため、今後の課題としてはグレブナー基底を用いた場合にメリットがあるか (グレブナー基底を使って解くことで早く解が求まる問題があるのか) などを調べてみたいと思います。