Mathematica はグラフ理論に関しては、早い時期から「組み合わせ論とグラフ理論」(1992年) という形でパッケージ化を試み、Ver 8.0 以降はパッケージを徐々に組み込み関数化し、その普及に力を入れてきました。本来であれば、そうした関数群を使い、Mathematica によるグラフ理論入門を試みようと画策したのですが、まずは具体的な応用を例にグラフ理論でよく使う関数を紹介するのにとどめることとしました。
発言順に関し、たとえば A が発言し、B が発言し、ついで A が発言した場合、A と B との間に何らかの近しい関係があると仮定できます。シェイクスピアの戯曲「アントニオとクレオパトラ」を参考に、アントニオを巡る人々とクレオパトラを巡る人々の関係の強さをグラフ理論を使い推定してみます。
発言リストは以下のような Excel データとして用意されています。
Excel データを Mathematica にインポートします。[[1]] は Sheet の1枚目を指します。
戯曲「アントニオとクレパトラ」は 42 シーンからなっています。
![]()
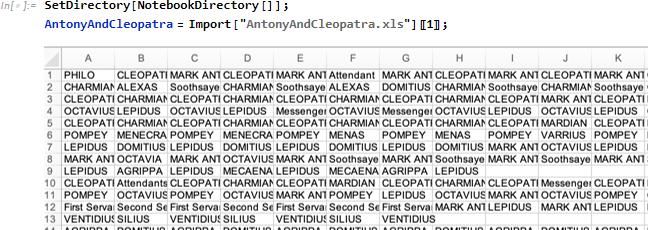
シーン1では、PHILO が最初に発言し、ついで CLEOPATRA が話し、MARK ANTONY が続いてます。

データ AntonyAndCleopatra から発言者がいない「" "」場合を除いたものを戯曲 play とします。
![]()
シーン1を scene1 とします。

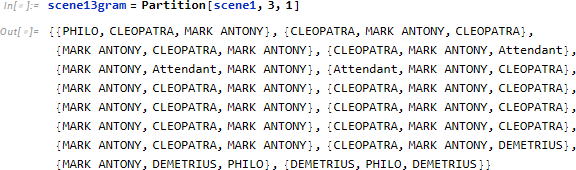
ここで、発言順における関係の強さに関する距離を3と仮定し、n-gram の組を求めることにします。scene1 における発言者リストを 3-gram に分割し、scene13gram とした場合、最初の 3-gram は {PHILO, CLEOPATRA, MARK ANTONY}、二番目の 3-gram は一人ずれて二人目から始まります {CLEOPATRA, MARK ANTONY, CLEOPATRA}。各 gram 内の発言者間には一定の親しさがあると仮定します。
全シーン play に対し (/@)、n-gram を計算し、各 n-gram s に関し、全二項組み合わせ (Permutation) を求め、同一発言者のペア ({a_, a_}) を DeleteCases によって削除し、全体を発言ペアからなる一次元のリスト S3gram を作ります。
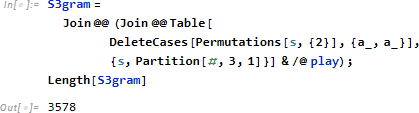
たとえば最初の4ペアを求めると次のようになります。
![]()
つぎに発言者ペアが何回登場するか調べます。ペアの個数が多いほど、直近で会話している回数が多い (互いに近しいと想像できる) ことがわかります。なお、Sort は Tally を求めるために使用しています。
![]()
ここでペアの登場回数の例を挙げると CLEOPATRA と PHILO との間ではわずか2回しか会話が交わされていないのに対し、CLEOPATRA と MARK ANTONY との間では 262回も会話があったことがわかります。
![]()
二項関係は、各項を頂点 vertex とし、関係を辺 edge としてグラフとして表すことができます。本来グラフは頂点リストと辺リストを必要としますが
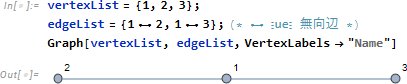
孤立頂点 (どの頂点ともつながっていない) がなければ辺のリストのみからグラフを構成できます。その際、無向辺リストは次の式で作れます。


以上で発言順から推定される関係グラフ g が得られたので、発言の重みを可視化したグラフ (発言力の高さに応じて頂点サイズを大きくする) を作ってみます。まず最初に各頂点 (発言者) に発言回数に応じた重み vertex[v1], vertex[v2] を分配します。

最後に各頂点の大きさ VertexSize を vertex[#] で置き換える作業を行い、辺の描画透明度を Opacity[0.2] と決め、その他オプションすべてを SetProperty によってグラフ g の属性として再設定します 。
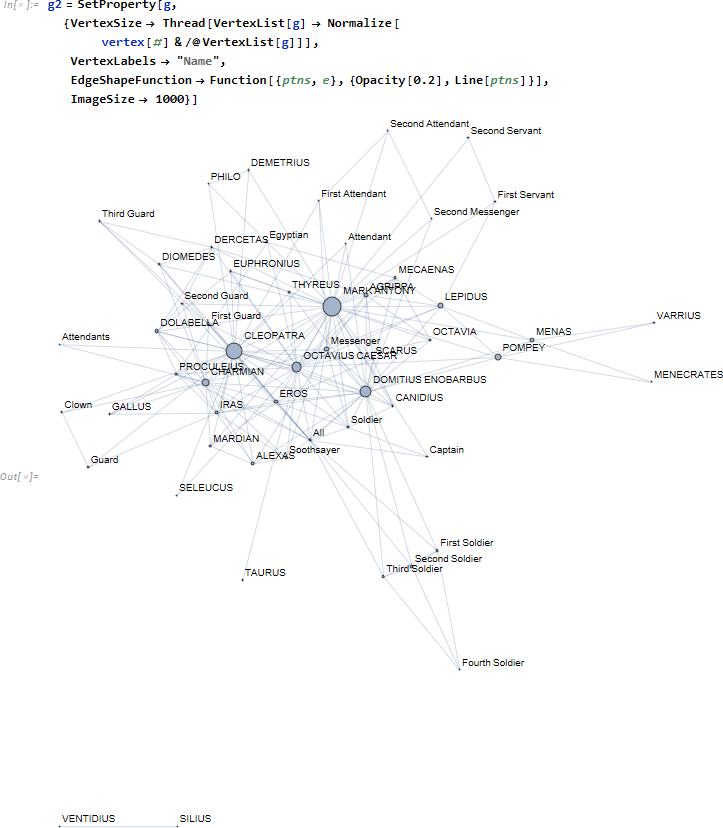
この結果から CLEOPATRA、MARK ANTONY を中心に、DOMITIUS ENOBARBUS (アントニオの友人)、OCTAVIUS CAESAR らが中心人物となっていることがわかります。
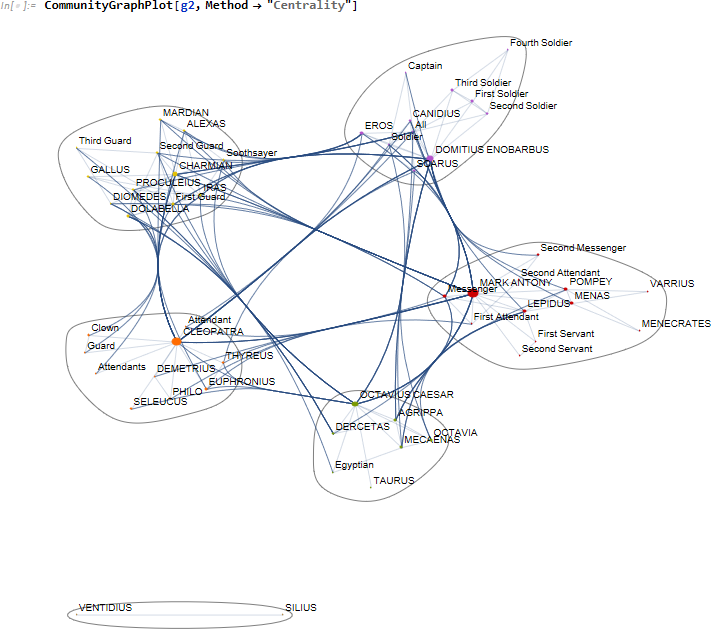
一方、同じグラフをコミュニティという概念で分割することができます。

最後の {SILIUS, VENTIDIUS} を除くと5つのコミュニティに分割されます。
![]()
CommunityGraphPlot を使うと各コミュニティの中心人物がハイライトされます:CLEOPATRA、MARK ANTONY、DOMITIUS ENOBARBUS、OCTAVIUS CAESAR に加え、CHARMAN (巫女) が新しく加わります。
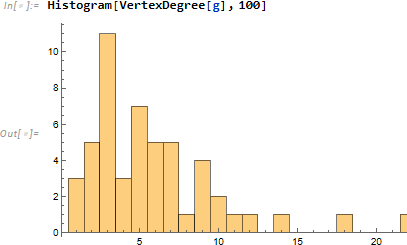
次のヒストグラムは戯曲 play で描かれたコミュニティにおいて、横軸は頂点次数 VertexDegree (つながり) の大きさを、縦軸は当該次数に対応する人数を表します。たとえば多くの人が3人のつながりなのに対し、18人のつながりを持つ人はわずか1人だというのがわかります。
一方、Mathematica が ExampleData に用意するミニインターネットでは
![]()
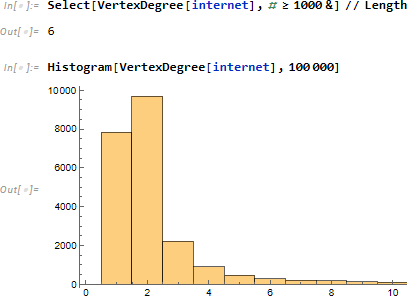
全頂点 22963 個に対し

頂点次数が 1000 以上の頂点はわずか6個しかありません。逆に頂点次数 (他の頂点とのつながり数) が2以下のものがほとんどだとわかります。
Mathematica には様々な中心性メトリックスが提供されていますが、ここでは媒介中心性(情報媒介強度)を使い、

中心性最大の頂点4の隣接グラフを描いてみます。

媒介中心性の値が 100,000 以下となる頂点番号 8179 の近接頂点 2493, 8178, 8180 からなる隣接グラフを描いてみます。

クリークは完全部分グラフで、グラフ頂点同士には一定の相関があると考えられます。たとえば、この例で同期して変動する銘柄、つまり、クリークを構成する銘柄を探します。最初にダウ・ジョーンズ工業株一覧 dji を用意します。

まず、2012年初からの利益 r を得ます。
ついで、情報が欠損しているデータ位置 pos を計算し、利益 r (実値 Values) を再計算し、
![]()
あわせて dji から欠損銘柄を削除します。
![]()
最後に利益をベースに全銘柄の共分散行列 cor を求めます。
![]()
次に、共分散行列 cor に関し、対角行列を 0 にし、選択した θ より高い相関係数を持つ部分に 1 を、低い部分に 0 を代入した隣接行列を用意します。

AdjacencyGraph は頂点リスト dji に対し、隣接行列で 1 が立っている頂点間を辺でつなぎます。
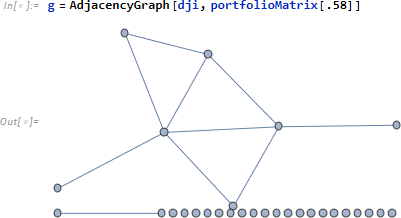
FindClique によって利益に関し同期して動くことが多い3つの銘柄を得ました。
![]()
変動同期に関し、累積利益グラフで確認します。

MorphologicalGraph は対象となる線画の結合部分をエッジ化します。ここでは迷路をエッジ化し、迷路を抜ける最短パスを見つけています。
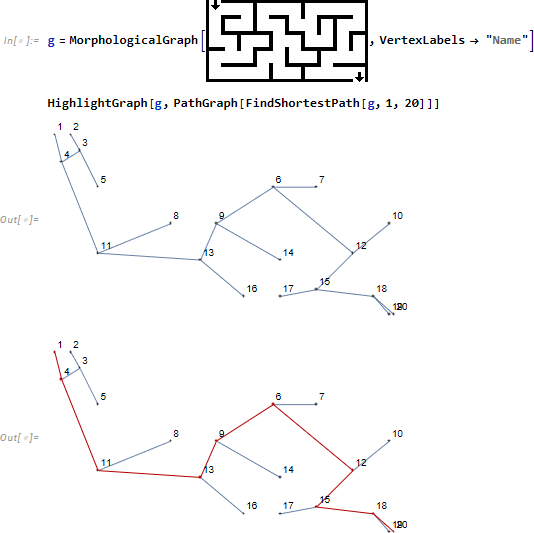
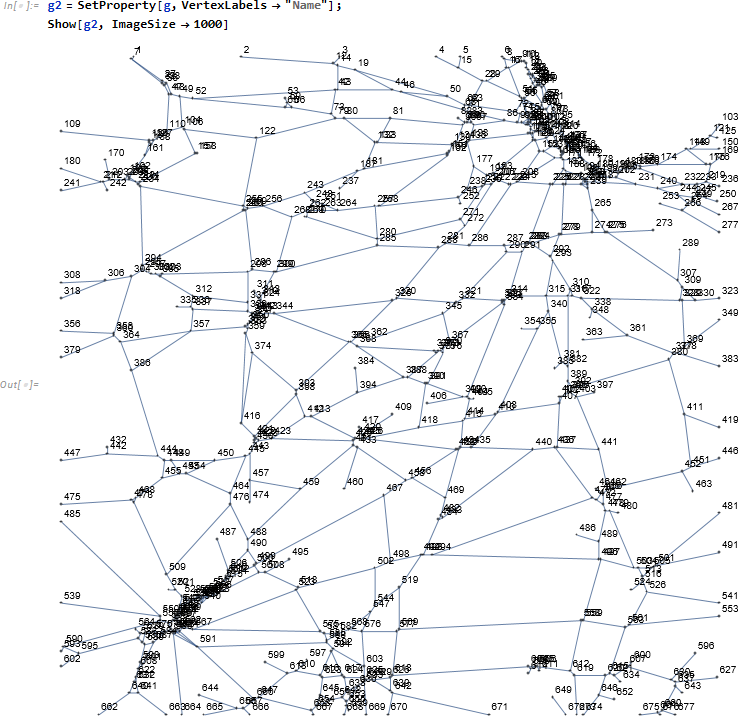
次はもっと複雑な線画ですが、発想は迷路の場合と同じです。

グラフとした場合の座標を確認しています。
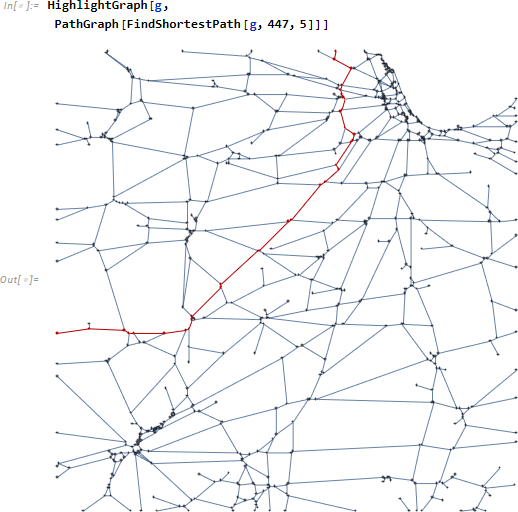
地点447番から地点5番までの最短経路を見つけ、元図にマップします。
Python コミュニティでは グラフ理論を利用した例題に関しては NetworkX が有望です。次回は NetworkX と Mathematica の比較を行う予定です。それとは別に、Mathematicaによるグラフ理論解説を次々回に紹介したいと思います。