Mathematica は非常に強力なプログラミング言語であり、計算の種類に応じた適切な関数セットが用意されていますが、その全部を使いこなせる人は残念ながら多くはありません。ここではその中でも重要な関数 (上記「Mathematica 関数」に列挙) を解説し、中置表記があるものについては紹介します。
本題に入る前に式の評価について確認しておきます。数値だけからなる式の評価は数値自身となります。
![]()
シンボル x からなる式の評価はシンボル自身となります。
![]()
ただし、具体的な値がシンボルに「束縛」されると、評価値は値自身となります。
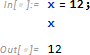
この部分だけみると = は通常のプログラミング言語にある代入と同じようにみえますが、Mathematica はこれを束縛と捉え、その束縛を解く関数 Clear を用意しています。
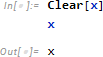
ちなみに関数 Remove は指定されたシンボルを名前空間から削除します。Clear しただけだと束縛は解除されますが、シンボル自身は名前空間に残ります。
![]()
Mathematica では記号 = は割当てと呼ばれ、= の右辺を評価し、その結果を左辺に束縛します。この場合、1行目で評価され r に束縛された「(乱数) 値」が、2行目 Table 内で置き換えられています。この段階で r の値は決しているので、すべて同じ値のリストが返ってきます。

= の代わりに Set を使って r を定義します。
![]()
:= で定義した場合、左辺のシンボルが「実際に使われる」時まで、評価が遅延されます (1行目) 。2行目で r の値を計算するたびに r は RandomInteger[100] と置き換えられ、遅延されていた評価が実行されます。

わかりやすく等価な式で書き直してみます。

あるいは

:= の代わりに SetDelayed を使い r を定義します。
![]()
なお、他言語で使われる「変数」は Mathematica では正式には「シンボル」と呼ばれますが、特に混乱を招かない場合、通常は変数で済ませます。ただし、数式処理システムとしての役割 (値を持たない変数が式に含まれていても計算可能) を強調するとき
![]()
は「シンボル 」 (今の場合、シンボル x) を使います。
関数は f (x )=x+1 のように名前 (ここでは f ) をつけて使うイメージがありますが、関数の本質は引数と本体のみで、Function はこれを実現します。次の例は、仮引数 x 、本体 x^3+1 からなる関数に実引数 2 を渡し、結果 9 を得ます。
![]()
この例は2つの仮引数 x と y からなっています。実引数 2 と 3 を得て、結果 13 を返します。
![]()
関数定義に関数名が不要なように関数引数名も不要で、代わりに「位置」に関する対応づけさえできればいいことがわかります。# はスロットと呼ばれ、関数引数に対応します。次の例では実引数 2 がスロット # に代入され、その3乗+1が計算されます。
![]()
次は 2 が第1スロット、3 が第2スロットに代入されます。
![]()
この形式は Python でも使いますが、Mathematica では新しい書き方です。
![]()
連想形式のデータに対してはキーワードをそのままスロット名として使うことができます。

Mathematica では計算は置き換えを行っているにすぎません。すでにみた例でいえば、r は1回評価され決した値で置き換えられていますが、

次の例では、すべての r がいったん RandomInter[100] で置き換えられ、その評価値が結果に残ります。

以上は exact な値同士で置き換えが起きましたが、同様なことをパターンを介して行うことができます。例で説明します。これは2個の引数 (値は何でもよい) を受取り値1を返す関数 f を定義します。
![]()
引数の数があっているので答え1を返していますが、
![]()
これは引数が1つしかないので、「未評価」として入力がそのまま出力となって返ってきます。
![]()
「_」は blank と呼ばれ、引数パターンとして使われます。パターン「__」 (blank 2個) は1個以上の引数にマッチします。この場合、3引数にマッチし、結果 2 を得ています。
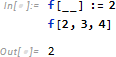
パターン「___」 (blank 3個) は0個以上の引数にマッチします。この例は引数0個の場合です。
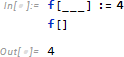
ではマッチした引数を関数本体 (右辺) で使いたいときはどうすればいいでしょう。引数にシンボルを追加します。2 が x にマッチし、3 が y にマッチし、2 + 3 = 5 を計算します。
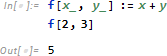
次の例で Sequence は引数列を表し、リスト式の中で組み込んで使うことが多いです。

最後にこんな例はどうでしょう?
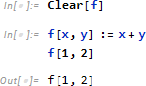
ここで関数 f は (blank _ がないため) 引数に「シンボル」x と y そのもの を期待しています。引数 1 と 2 は x, y にパターンマッチしないので未評価として f[1, 2] を返してます。では、どんな場合に、このパターンにマッチするでしょうか。簡単です。実際にシンボル x と y を渡せばいいわけです。
![]()
Function を使い関数を定義できますが、引数に様々な制約を与えるには Head 形式 (
Function[x, x+1]に対し
f[x_]:= x+1
) で関数を定義する必要があります。
たとえば関数
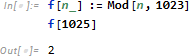
で引数 n が取る値を整数に限定したいとすると Mathematica では次のような書き方ができます。
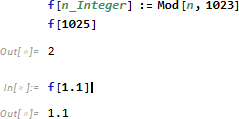
あるいは任意の真偽値を返す関数、たとえば素数判定関数
![]()
を使いたいときは 先頭に ? を付けて使います。

オプション引数について簡単に説明します。
![]()
関数 f が次のように定義されています。
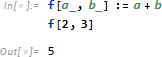
しかし引数 b はたいていの場合、値1をとると分かっているとします。その場合、次のように記述することで関数 f を呼び出す際、b に対応する部分を省略 (オプション) することができます。
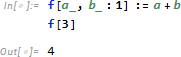
ただし具体的に b の値を指定すれば その値が a + b で使われます。
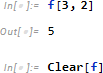
Map はいまやどのプログラミング言語でも一般的になってきましたが Mathematica では ver1.0 のときから導入されています。仕掛けは単純でリストの各要素に同一関数を適用した結果のリストを返します。たとえば、リストの各要素を2倍するには次のように書きます。
![]()
Map の中置形式 /@ を使うと次のように短く書けます。
![]()
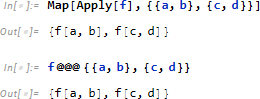
ただし2引数を想定した場合、/@ をそのまま使うことはできず、次のように @@@ (MapApply) 書かなければなりません。
![]()
あるいは
![]()
なぜ Apply を必要とするのでしょう。#1+#2& を関数 f としたとき、Map[f, {{a,b}}] に対し、f{a,b} (エラー!) となるのを、 Apply[f, {a,b}] = f[a,b] によって防ぐためです。
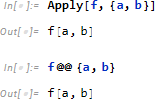
以上を整理し直してみます。
ここで Map 関数を Grid および Partition と組み合わせたこんな例を紹介します。素数を囲む四角は Framed を使い作っています。

/. の左辺に対し、![]() の左辺で指定した変数を
の左辺で指定した変数を ![]() の右辺の値で置き換えます。
の右辺の値で置き換えます。
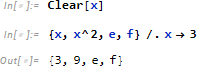
![]() は先に右辺を評価し、その結果で置き換えるのに対し
は先に右辺を評価し、その結果で置き換えるのに対し
![]()
![]() では、
では、![]() の左辺 (今の場合、
の左辺 (今の場合、x) の置き換えが起きるたびに、右辺 (今の場合、RandomReal[]) が評価され、代入されます。
![]()
関数形式 f[...] に対し、引数が1個以上のもの「すべて」を "OK" で置き換えます。
![]()
引数が0個以上 (3個の下線 ___ で表す) のものすべてを "OK" で置き換えます。
![]()
与えられたリストに対し、負の要素を w で置き換える状況を考えてみます。この例は次のように読みます:{6, -7, 3, 2, -1, -2} の要素を x で置き換えます。ただし、この状況では x が何を指すのか不明です。続けて /; 以降をみると具体的に x が指定 (0未満) されています。ついで、そんな x を w で置き換える指示を Rule -> によって出しています。
![]()
与えられた整数ペアに対し、共に素数だけのペアのリストを返します。
![]()
![]()
関数 f を変数リスト varList と値リスト valueList に適用し、串刺し f[x, 1], f[y, 9], f[z, 11] からなるリストを作ります。
![]()
たとえば関数として Rule を適用した場合はこうなります。
![]()
同じことを中置形式で作ります。
![]()
MapThread
![]()
は基本、Thread と同じです。
![]()
ただし次の例のように Thread 対象をリストの深さで選ぶ場合には MapThread を利用します。
![]()
与えられたリストから整数要素のみを集めたリストを作ります。
![]()
整数以外 (実数) のリストを返します。
![]()
リストを要素とするリストからペアだけを集め、当該ペアの要素の和からなるリストを返します。
![]()
{1,2,4,7,6,2} の各要素 # に対し、2より大きいものを集めリストで返します。
![]()
{{1,2},{2,4},{99,5},{3,1}} の各要素、たとえば {1,2} に対し1番目が2番目より大きいものだけを集めます。
![]()
整数リスト A に対し

素数だけを取り出したリストを計算します。 (AppendTo は副作用として第1引数に第2引数が追加される。)

同じことを、 Sow で条件に合致する対象を囲い込み、一番外側の Reap で回収します。ここで # は A の各要素に対応します。

Reap / Sow は表現が簡潔というだけでなく、AppendTo による明示的なメモリ領域操作を使わず、システム内に確保されたバッファ領域を使うため、処理時間も短くなります。
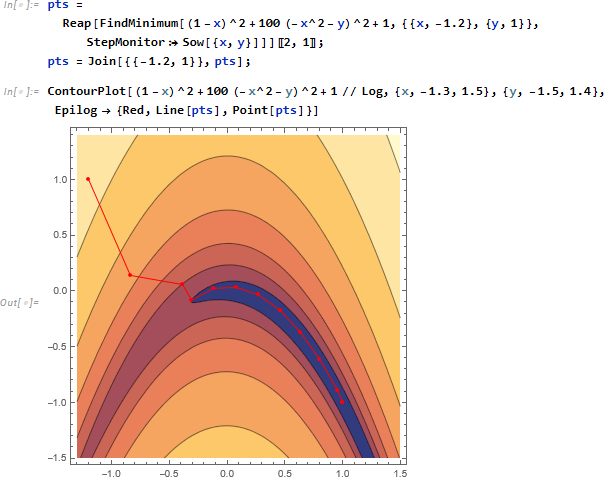
次は関数 FindMinimum のヘルプから引用する例ですが、FindMinimum が行う近似計算の途中解を Sow で集め、最終的に Reap で回収した内容を pts に代入し、元式に対応する等高線プロット上に pts の軌跡を描画します。
たとえば次のような例、x の初期値 0 に対し、1 を1万回加える、を考えます。
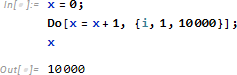
これに対し Nest 関数を使ったものを紹介します。Nest 関数は NestList 計算の最後の値となります。次の例は初期値 0 に対し、関数 plus[#,1]& を3回自己適応します。つまり、# には最初 0 が入り、その結果 plus[0,1] が再度 # に入り、plus[plus[0,1],1] となります。これを3回繰り返します。
![]()
上記 Do 形式の式を Nest 形式で書き直してみました。
![]()
Nest 形式は単にコードが短くなるというだけでなく、計算速度も上がります。理由はスロット # にあります。次の最初の例では変数 x への明示的な参照が100万回起きます。
![]()
一方、スロット # には明示的なメモリは割り当てられることはなく、この例では約10倍の高速化が図られています。
![]()
あまり使い道はありませんが、Nest を使うと、こんなトリッキーな例も作れます。
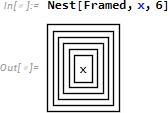
連分数をつくってみます。
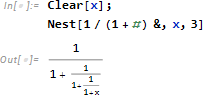
最後は、このような形状をもった図形
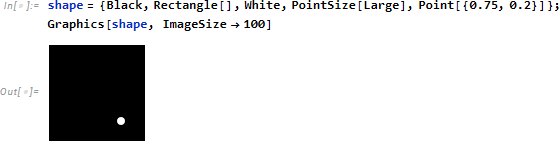
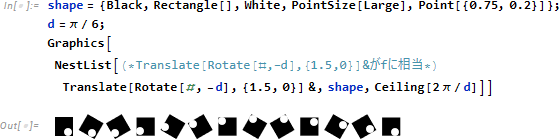
を、NestList

を使い、回転移動させます。Rotate によって回転させながら、Translate によって位置移動を行っています。
FixedPoint 関数は Nest と類似します。違いは自己適用において事前の値と現在の値が等しくなると自動的に繰り返し適用を終了する点にあります。次の例は自己適用計算を15回繰り返しています。ただし、後半は同じ値 2 が続いています。
![]()
これに対し、FixedPoint を使い、終了までの回数を 1000 として動かしましたが、同じ値が2回続いた (最小不動点に到達した) ため計算は終了します。
![]()
次の例はニュートン法によって ![]() の値を求めてます。なお出発点は 1.0 とします。
の値を求めてます。なお出発点は 1.0 とします。
![]()
階乗計算について考えてみます。
![]()
Do を使い計算し、同じ結果を得ます。
![]()
同じことを Fold を使って実現します。ここで #1 は n に、#2 は k に対応します。

なお、Fold も Do を使った計算より高速になります。
次の例では 1010より後で最初に来る素数を見つけます。Break はそれ自身を囲む最小単位のループから脱出するのに対し、Throw は任意の深さから Catch までジャンプし脱出します。かつ、Break が単に繰り返しを中断するのみなのに対し、Throw は値を持ち帰って処理を中断します。

長年 Mathematica を使ってきて、これだけ知っていれば Mathematica 通と呼ばれる関数たちを紹介しました。それでももしかしたら取りこぼしがあるかもしれません。普段お使いの中で、この不明な記号や関数があれば、ぜひこちらまでご連絡いただければ幸いです。ある程度、溜まった段階で、「Mathematicaらしい関数」第2段を出したいと思います。