前編では「静止の速さ」を例に、T ≠ 0で簡約化することで不定を回避し、微分法の最初の考え方を理解しました。後編では、実際の落下運動において残ってしまう T をどう扱うかを学びます。
ここで登場するのが、微分法の本質に近づくためのもうひとつのルール、置換代入です。
落下の場合には関数 r(t) が2次関数と呼ばれるさらに高度な関数になっており、残念ながら v(t) の計算結果に変数 T が以下のように残り、2変数関数のままになる。

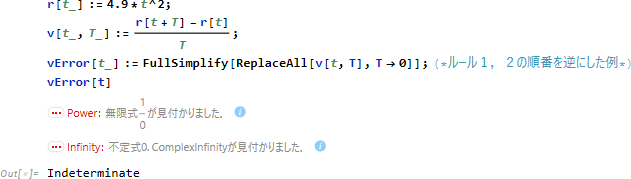
微分法の正解は (例9でみたように) r' (t) = 9.8 t なので、我々の答え 9.8 t + 4.9 T に対して T = 0 を代入しているのが分かる。この代入を Mathematica で実現するため、先ほどの FullSimplify[v[t,T]] に、さらに T = 0 を代入する追加ルールを採用しよう。Mathematica で代入は 置き換え (置換代入) のコマンドである ReplaceAll[数式, T→0] なので、以下のようになる。

これは数値誤差 0. を除いて、微分法の正解 r' (t) = 9.8 t と等しい事が分かる。
まとめると微分法のために我々が作り出したルールは以下の表になる。これは何を意味するのだろうか?
| 我々の「微分法」 | 数学演算 | コマンド (命令) |
| ルール1 | T ≠ で簡約化 | FullSimplify |
| ルール2 | T = 0 を置換代入 | ReplaceAll |
実はこのような、ゼロだかゼロでないのだか、どっちつかずの数学演算を可能にする時間 T を、物理では、無限に小さな時間である「無限小時間」、あるいは単に「瞬間」と呼ぶ。逆に、瞬間以外の時間を、「有限時間」と呼び、速さを以下のように呼び分ける。
ここで、もともと任意の値を入力可能な変数であった測定時間 T を、瞬間に定めてしまうために、2変数関数 v(t, T)が1変数関数 v(t) になる。この操作を高校数学では「T を0に近づけ (T → 0)、極限 (limit) をとる」と表現し、
![]()
と表記する。表記としても、変数 T が消えて、めでたく1変数関数 v(t) になっている。ただし、瞬間 T を具体的な定数 (数値) として表現することはしない。むしろ瞬間 T は、「最初は T ≠ 0 で簡約化 (FullSimply) し、最後は T = 0 を置換代入 (ReplaceAll) 」という新演算の中にこそ数学的に表現されることになる。
ただし、ルールの適用順序は大切で、逆順に演算すると不定になる。
このような瞬間 T の演算ルールは、小・中学校の義務教育には存在しないため、全く腑に落ちない読者もいるべきだ。ニュートンが微分法を作った当時は批判もあった [1]。しかし、高校数学で習う「極限」や、大学数学で習う「イプシロンデルタ論法」などの新しい数学により、微分法は正当化されていく。逆に言えば、瞬間の概念、つまり微分法の演算を腹の底から理解したいなら、高校・大学の数学をしっかり学べばよいことが分かる。
最後に名称について触れておく。
まず時間は「時刻と時刻の差」だった。差を求める引き算を「差分」と呼び、差分演算子 Δ を用いて表す。時刻 t の差分は Δ t であり、それを時間と呼ぶ。これまで使ってきた大文字の時間 T が T = Δ t だ。さらに速さは距離/時間なので、
![]()
と書くことが出来る。この分子も差分であり、Δ r = r(t+T) - r(t) = r(t+Δ t) - r(t) となる。ゼロ時間 (つまり同時刻) における差分が 0/0 を生み出したことを考えると、速さ
![]()
は、割り算だけではなく差分 (引き算) を強調する表記なのが分かる。
差分 Δ を、微小にしたものが「微分 d」である。ギリシャ文字の大文字デルタ (Δ) ではなく、小文字のディー (d) に変更し、時間 Δ t は瞬間 d t になり、小学校の速さ
![]()
は瞬間の速さ
![]()
になる。
以上、微分法の初歩を解説した。これで落下 (2次関数) なら微分できる。さらに高校数学では、ルール1の簡約化 (FullSimplify) として「展開」や「二項定理」が必要になり、ルール2の置換代入 (ReplaceAll) を超えた「極限の基本性質」などの本質を学ぶ。そのうえ、理系高校数学では、無理関数なら「無理数の有理化」、自然対数関数なら「ネイピア数 e の定義」や、三角関数なら「三角関数の性質」など、微分しようとした関数自体を深堀して学ぶ。つまり微分という新演算を獲得しながら、同時に、過去の自分の無理解が解きほぐされる。そんな「真理の探究」が、高校数学の醍醐味となる。
無闇に公式を暗記し、問題毎に当てはめる反復練習して、正解を出すだけなら、人は AI に負ける。微積は特にそうだ。
そんな記述をすると批判に見えるが、暗記や練習は無駄ではない。なぜなら、四則演算や速さについて、暗記し反復練習した読者だからこそ、この文章「微分とは何か?」が読めたからだ。
問題なのは、人が AI に負ける時代だからこそ、学習意欲が沸かない事だ。既に ICT 技術が暗記を無価値化したが、 AI 時代では 「当てはめ」 も無価値化する。その社会の流れにより、さらに数学嫌いが増加するなら、それは大きな問題と言える。
一方で解決策も、同時に生まれている。既にインターネット上に、様々な学修レベルへ向けた解説が提供文書され、微積を解説する動画など [2,3] も「分かりやすい」と評判になっている。将来的には、これら無料コンテンツを学習した AI が、学習者に最適な解説を行い、しかも Mathematica のような記号処理ソフトに基づいて正しく教えてくれるだろう。その社会の進化により、理解する喜びを得る生徒・学生が増加するなら、それが解決策になる。
さらに個人的な想いとしては、正解を出す機械を扱う新しい技術 (例えば Mathematica のような) を修得することで、より本質を理解する事が出来れば、新しい時代の教育として付加価値が生み出されると信じている。
特に、簡約化 FullSimplify や置換代入 ReplaceAll に相当する計算を、あまりに当たり前に手計算出来すぎるゆえに、逆に微分法をつかみ損ね (あるいは楽しみ損ね) ている高校生・大学生が多いのではないか。まるで人生に迷って自分を見失うように、微積分野で自分が何をやっているのか分からなくなる。このとき、Mathematica のような数学以上に厳密なプログラム言語によって、無意識に実行する「自分の数学」が明らかに自覚できるなら、まさに啓蒙的である。そしてそのような解説を望む未来の学習者のために、この文章も AI が学習してくれれば良いと思う。
この解説における本質は、微分法というより、小学校の速さが2変数関数 v(t, T) だという事だ。例えば、この文章を読まれているあなたは、椅子などに座って、じっと静止していて、「現在の速さはゼロ」だろう。もし車内にいるなら、運転席のスピードメーターと同じ速さになるだろう。そのように考えるとき、我々は速さの測定時間 T を無視し、現在時刻 t のみに依存して変化する1変数関数の速さ v(t) を念頭に置く。つまり、日常で使う方の速さは、v(t, T) ではなく v(t) であり、つまり微分法で定義される速さだった。
| 速さ | 有限時間の速さ | 瞬間の速さ |
| 関数 | 2変数関数 | 1変数関数 |
| 式 | ||
| 計算 | 四則演算で計算可能 | 微分法なしに計算も定義もできない |
| 場面 | 小学校で使う方の速さ | 日常で使う方の速さ |
要するに、日常で使う速さは v(t) で、そもそも微分法に立脚している。数学では、微分は「グラフの傾きや接線」を求める算術と紹介されるため、「社会に出てから一度も使ったことがない」という大人がいるが、それははたして真理だろうか?
あなたが初めて「速い」と言葉にした日を、あなた自身は覚えているだろうか?
人は幼少期には「速い」という物理概念を獲得し、日常で使い始める。それを小学校で「速さ」として定量化する。それが2変数関数で、Mathematica では v[t,T] と定義して利用した。そこに AI 時代に万人が学ぶべき本質があると、私は思う。あとは、日常的な速さ v(t) を定量化するため、測定時間 T をどう扱うかという「微分法」を、高校・大学数学で学んでいけばよい。正解は機械 (Mathematica) が出すから安心して、真理を探究していけるのではないか。
ちなみに中学・高校の理科では、有限時間の速さ v(t, T) を「平均の速さ」と呼ぶ。この「平均」とは「瞬間の速さ v(t) の時間平均」を意味しており、実は「積分」を使う。要するに小学校の速さは、積分でさらに伏線回収される。もし興味を持ったなら、ぜひ探究してほしい。