Mathematica を使うと、与えられたデータ列に対し、データを生成した背景 (モデル式) を推定できます。このとき、データのみからモデル全体を推定する場合と、データに対しモデルを明示し、モデルパラメータのみを推定する場合の2タイプがあります。FindFormula はデータのみからモデル式を生成してくれる強力な関数ですが、高い確度は期待できません。また、モデルを線形結合に限定すると LinearModelFit はデータのみからモデル式を推定してくれます。モデル式が非線形の場合は NonLinearModelFit 関数を使い、データのみならずモデル式を明示します。あと NonLinearModelFit とほぼ同じですが、正則化によって精度調整できる FindFit という多機能 Fit 関数を紹介します。なお、Mathematica において最初に提供された Fit 関数については今回は紹介しませんが、Fit の概要を理解するのに役立ちますので、ぜひ、参照されることをお勧めします。
FindFormula は与えられたデータ列({x, y} のリスト)に対し、プロット近似する関数を見つけ、返します。次の例はデータ列 {1, 5}, {2, 4}, {3, 3}, {4, 2} に対し、プロット式 6-x を推定します。つまり、x=1 から 4 までは 6-x でプロット値を推定できることを表します。
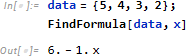
これに対し、次の例では FindFormula を実行するたびに異なる区間に分割されます。毎回異なる理由は、推定初期値がランダムに設定されるからです。また、区間に分割される理由は、情報が少ない (x=1, 2, 3 までは線形だが、x=4, 5 の情報がなく、唐突に x=6 の値が現れ、かつ、これで情報が尽きている) ためです。それでも FindFormula は推定解を生成します。なお、FindFormula は3次元以上のデータには使用できません。
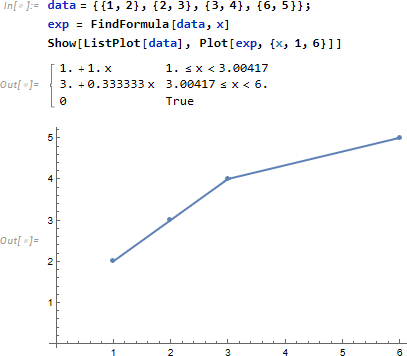
次は、x=-10 から 10 までの範囲に対し Log[2 + 3x^2] を y 値とし、さらにノイズ (0 から 0.5 までの一様乱数) を加えた複雑なデータを用意します (SeedRandom[1234] は生成される乱数列を固定するため)。
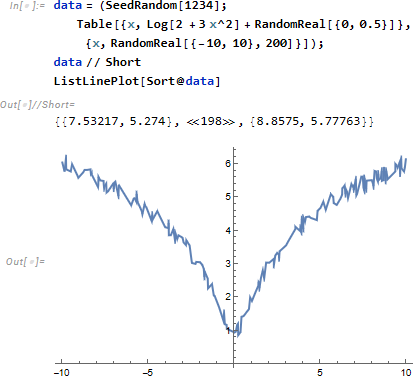
こんな複雑なデータに対しても FindFormula はプロット式を推定してくれます。
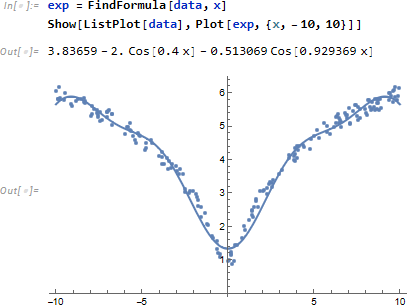
ただし評価のたびに異なる推定式を返してきます。
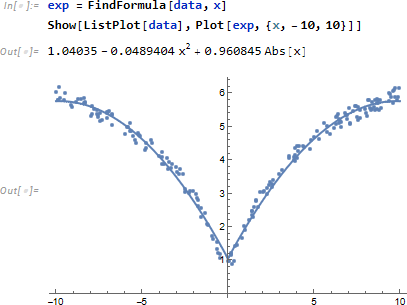
いま見てきたように FindFormula は与えられたデータに対し、複数のプロット式を推定します。次の結果は許される関数をすべて使い (TargetFunction->All)、すべて (All) の評価基準 Score/Error/Complexity を表示してます (なお、この結果は Mathematica の DataSet の形式になっています)。
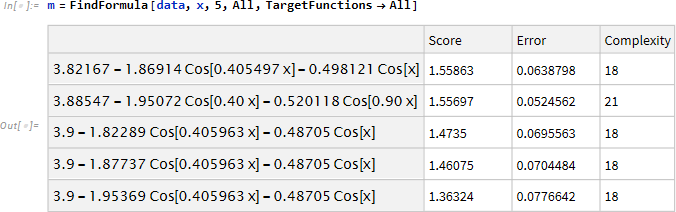
ここではエラー (誤差) がもっとも小さくなる対象を選択し、

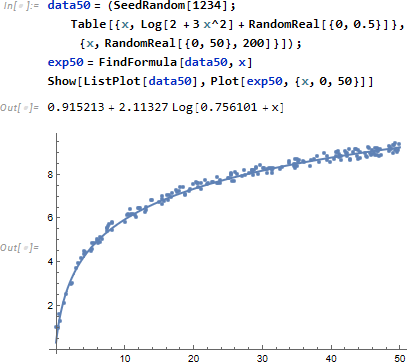
当該式を取り出し、exp とします。
![]()
式 exp を実際のデータプロットを重ねてみます。良さそうに見えます。
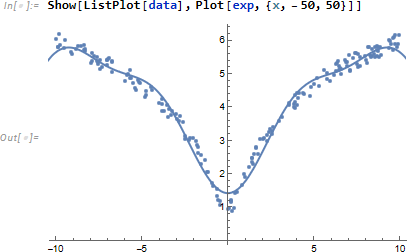
良さそうに見えますが、データ範囲を {-10, 10} から {-50, 50} に広げると、推定式がアンダーフィッティングしてることがわかります。
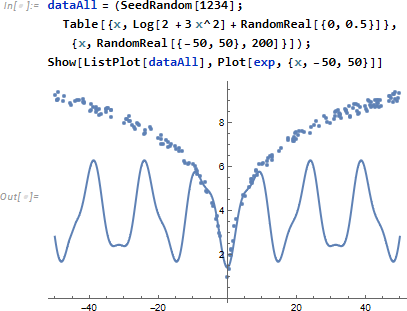
(原データは x=0 で特異点を持っていませんが)データ範囲をあえて x >= 0 に限定するとデータ生成に使用した Log を含む式を得ます。
FindFormula は線形、非線形を問わずデータに Fit する式を推測してくれましたが、データの次元数は2に限定されます。一方、線形 Fit に限定すれば LinearModelFit は多次元データに関し、プロット式の推定を可能とします。たとえば4次 (3次のデータとその線形結合 4i + 2j + 3k) なる仮想のデータを用意し、

i, j, k の係数を推定すると、4, 2, 3 の近い値となる、つまり一定の範囲で推定がうまくいっていることがわかります。

最適 Fit の式を取り出します。
![]()
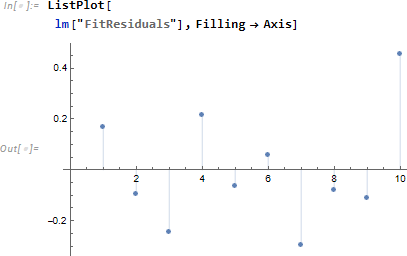
ただし Fit 残差 residulas 適用範囲の可否を実際の応用において判断する必要があります。
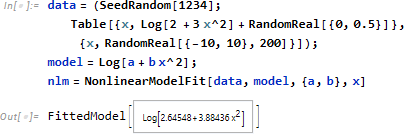
NonLinearModelFit は LinearModelFit と異なり、Fit 式を推定するためのモデルを指定する必要があります。冒頭で使用したデータを再度取り上げ、model (Log[a + b x^c]) に3つのパラメータ a, b, c を指定したところ、解に複素数が含まれるというエラーとともに失敗しました。そこでまずは c=2 を固定してみると、なんとか解 (a, b の値を推定) を得ることができました。
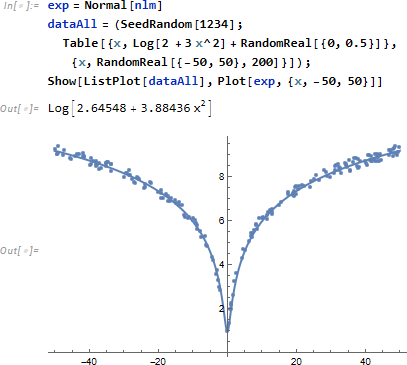
得られた結果を使い、今度は {-50, 50} の範囲まで拡張し Fit したところ、FindFormula で起きたようなアンダーフィッテイングは回避されることがわかります。
FindFit は非線形 Fit に関しては基本、NonLinearModelFit と同じですが、正則化オプション NormFunction を持つ点で異なります。正則化を行うことで、Fit 残差を縮めます、かつ使い方によっては NonLinearModelFit で生じたエラーを回避できる場合があります。ちなみにここでは推定パラメータに a, b のみならず c も指定しています。(正則化関数の詳細については NormFunciton を参照ください)

ここから先は様々なモデルへの対応例を紹介します。最初はモデル式が区間で与えられた場合です。
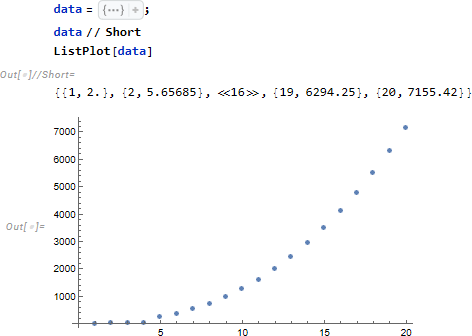
プロット点を眺めると x=5 前後で推定式の形が異なっていると見て取れるので、モデルを以下のように区間で分けて設定し、FindFit によってパラメータ推定を行います。
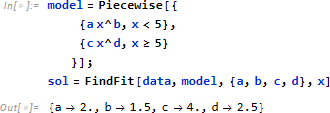
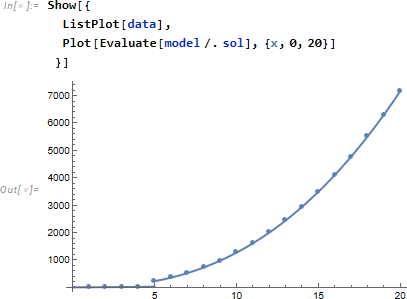
当然のことですが、x=5 においてジャンプが起きるので、あとは運用での判断に委ねられます。
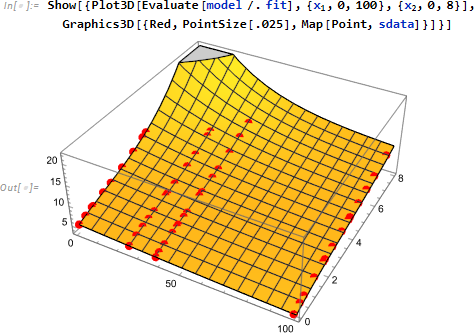
Mathematica が提供する潤滑剤粘度データ (第1引数=温度、第2引数=圧力、第3引数=粘度)

に対し、既知のモデル
![]()
を設定し、モデルパラメータを予測してみます。なお、モデルの条件付を向上させるために圧力データのみを 1000分の1 に調整します。
![]()
FindFit を使い、スケールされたデータに最もフィットするパラメータ θi を求めます。
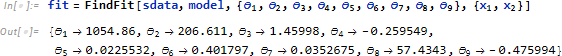
最後にフィットしたプロットをスケールされた実験データとともに示します。
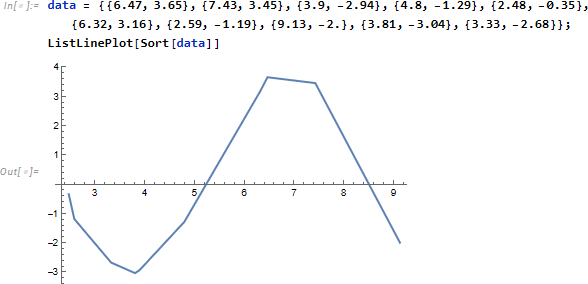
このデータセットに関し、2次の微分方程式
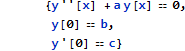
を想定し、パラメータ a, b, c を推定する事を考えます。他の場合と異なり、微分方程式自身を中核に据え、パラメータを引数とする関数として model を定義します。そして Fit 計算時、x を変化させながら微分方程式を解く (NDSolve)ことを繰り返し、データ系列にフィットする a, b, c を推定します。したがって model 引数 a, b, c が数値に限定するよう ?NumberQ を付けているのは意味があります。
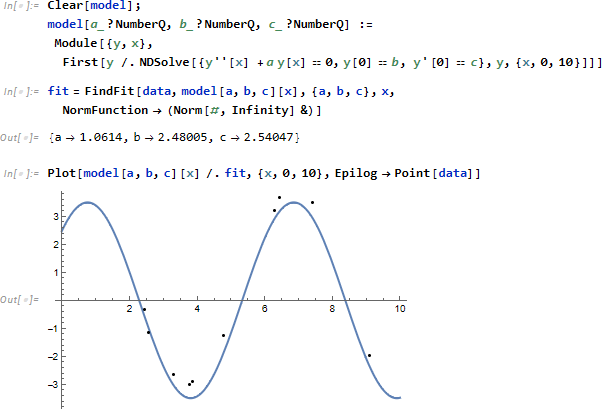
なお、上記計算は Module 部分を 8150 回計算するのに対し、一度計算したものを取っておくタブレーションという技術 (model[a, b, c] = ....) を使うと Module 部分の計算を約10分の1 (652回) に減らすことができます。
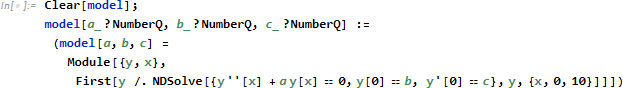
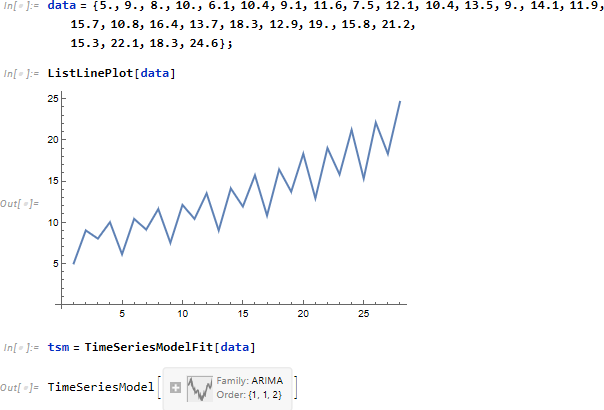
与えられたデータが時系列を形成することがわかっている場合は、TimeSeriesModelFit 関数が使えます。
ここでは ARIMA プロセスモデルを仮定しています。なお、プロセスモデルの詳細に関しては TimeSeriesProcesses を参照ください。
![]()
時刻 35 時点の推定値。
![]()
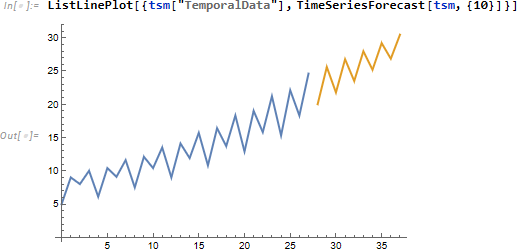
現行データから 10 手先までの予測値。
次回は、与えられたデータに関し、確率密度分布を想定し、確率密度関数を推定する話を紹介する予定です。