Mathematica にコンパイル機能があることは昔からよく知られていますが、いま一つ使い方がわからず、あまり利用されていません。本稿では具体的な例 https://reference.wolfram.com/language/ref/Compile.html.ja 内[おもしろい例題]を参考に、コンパイルすると高速化 (この例の場合は約30倍に高速化) されることを示します。
コンパイラを知らない人はいないと思いますが、コンパイルの基本がメモリ参照を CPU 内メモリ (普通はレジスタ) に切り替えると理解している方は少ないかもしれません。メモリアクセス速度を低い順に並べると
ファイル << メインメモリ < CPUレジスタ
となります。Mathematica は通常、インタプリタとして機能し、変数が登場するたびにメインメモリへのアクセスが発生します。これに対し、コンパイラは変数を CPU レジスタに割り付けるために、参照速度が上がります。
なおコンパイルにおいて当該データが何バイト使用するか事前に知る必要があり、Mathematica のコンパイル関数 Compile では引数に必ず型を加えます。たとえば、{x,_Real} 「引数 xの型は実数」はその例です。
したがってコンパイルの対象変数は実行時、整数や実数等の数値でなければなりません。ただし、それらの変数が Sin 等の組み込み関数の引数あるいはリスト構造の一部であっても、コンパイルの効果はあります。
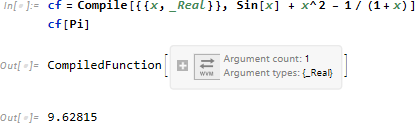
式 Sin[x] + x^2 - 1/(1+x) を本体に持つ関数 cf を定義します。
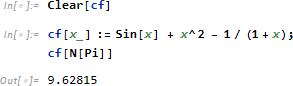
この関数の本体部分をコンパイルするには引数部分 {{x,_Real}} (二重括弧は複数の引数を想定) を含め、本体を Compile で囲みます。結果の CompileFunciton が代入された変数 cf は通常の関数名として使用できます:8cf[Pi] 。なお、引数が数値を仮定しているため、シンボル Pi を N によって強制的に数値化する必要はありません。
ここでコンパイルの効果をみるために、かなり不自然な関数 (同じ計算を100万回
繰り返す) を定義します。現在、Mathematica の Do 関数はかなり最適化されていますが、それでもコンパイルするのとしないとでは約10倍の速度差が出ることがわかります。

以下の各小節に「原コード」と「コンパイル化コード」を挙げますが、その前に関数引数部分に関し、コンパイル化前と後の比較を行います。なお With は一時的な値を設定するのに使用し、Block のように内部の変数を局所化しません。つまり With 内で関数は大域的に定義されます。
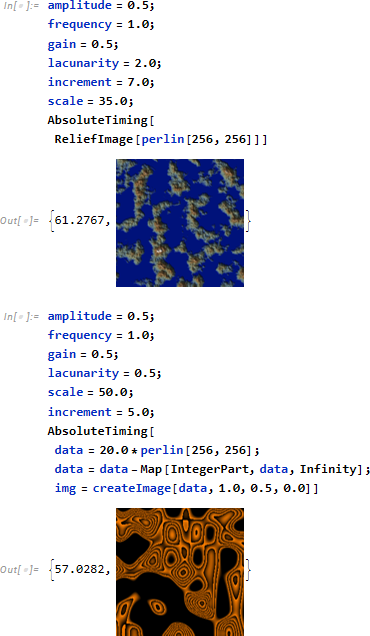
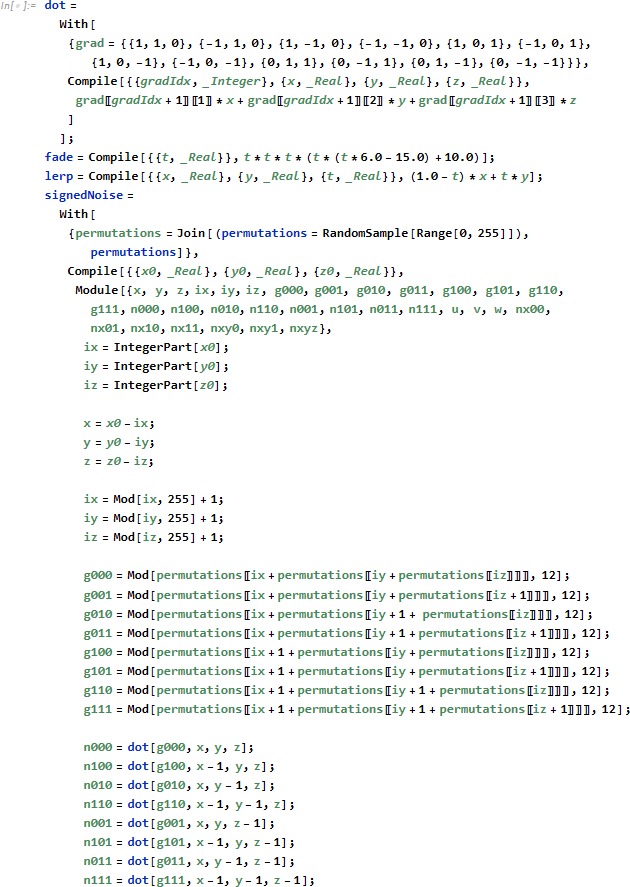
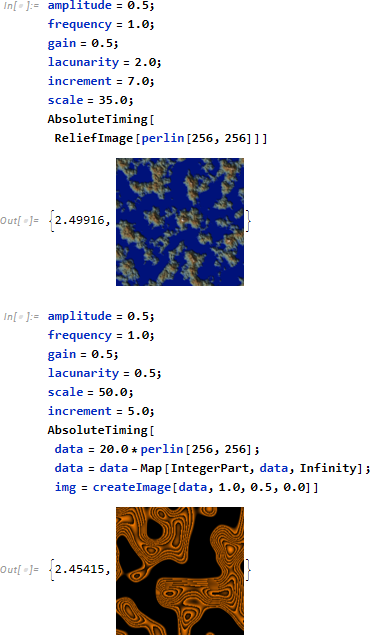
![]()
![]()



比較4.比較5.ではコンパイラオプション
![]()
が指定されています。
CompilationTarget はデフォルトでは C コードを想定します。ただし signedNoise のように計算よりリスト処理が中心の場合、Mathematica の仮想マシン用コード WVM を指定し、高速化します。
InlineExternalDefinitions を指定した場合、signedNoise 内で使用される外部関数 (たとえば dot 等) がインライン展開され、コンパイルされます。これによりコンパイルコードは長くなりますが、関数呼び出しが減る分、処理時間は高速化されます。