https://doi.org/10.3888/tmj.23-4
| Mathematica には、グラフ理論の研究を行うための多くの組込み関数があります。以前は、これらの関数にアクセスするために Combinatorica パッケージをロードする必要がありました。今ではほとんどが Mathematica の内部で利用できます。この記事では、いくつかのユーザー定義関数を紹介することにより、Mathematica を使用したグラフの頂点のカラーリングに関する問題を研究します。 |
頂点のカラーリングのみを考慮するので、色付きグラフは常に頂点が色付けされたグラフを意味します。
-カラーリンググラフは、頂点を 個の互いに素な部分集合に分割したものです。２色のカラーリングから始めます。カラーを赤と青にします。もし、２つの頂点が辺で接続されている場合、２つの頂点は neighbors です。同じ色の2つの頂点は friends と言い、反対の色の2つの頂点は strangers と言います。色付きの頂点の neighbors の半分以上が
の friends である場合、それは friendly neighborhood にあると言い、そうでなければ、 は unfriendly neighborhood にあると言います。もし、グラフのすべての頂点が同じ色であるなら、すべての頂点は friendly neighborhood にあります。すべての頂点が unfriendly neighborhood にあるような２色カラーリングはありますか？これから説明するように、この質問に対する驚くべき答えはイエスです。
グラフの２色カラーリングは、もし各頂点が unfriendly neighborhood にある場合、つまり、neighbors の少なくとも半分がそれ自体とは異なる色になっているなら、unfriendly です。すべての有限グラフが unfriendly なカラーリングを持つことは定理です。（状況は無限のグラフの場合はもっと複雑です［１、２］）。証明は巧妙です。しかし、それほど長くはありません。そして次にそれを示します。色付きグラフの mixing number を、頂点の色が異なる辺の数と定義します。続けて”反転”つまり、friendly neighborhoods の頂点の色を変更します。頂点を反転すると、他の頂点の neighborhood ステータスが変わることがあります。しかし、反転するたびに、グラフの mixing number が増加します。mixing number はグラフ内の辺の数によって制限されるため、この反転プロセスは、やがて反転可能な頂点がなくなる、つまり、friendly neighborhoods にある頂点がなくなる必要があります。
簡単な例から始めます。最初に、７つの頂点を持つ完全グラフを検討します。
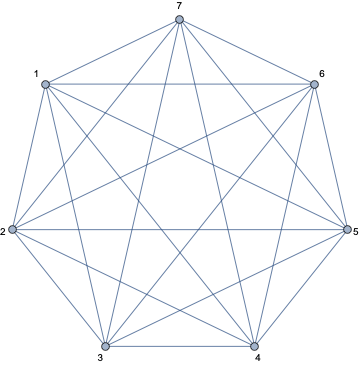
頂点を赤または青に色付けします。４つの青と３つの赤の頂点で始めると仮定します。
これが色を示す方法です。
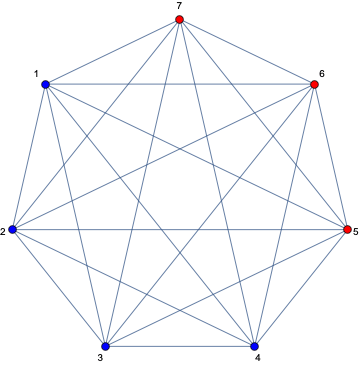
mixing number を計算するために、最初に辺の集合を生成します。
次に、辺の頂点の色が異なるかどうかを判断する
を導入します。
次に、 は頂点の色が異なる辺を取り出します。
最後に 
を 
に適用します。
これがの mixing number です。
の他の２色カラーリングを考慮することで、このカラーリングがグラフの最大 mixing number を持つことが容易にわかります。したがって、このカラーリングは unfriendly でなければなりません。一つの色が４つと他の色が３つの場合は、
の mixing number を与えるように、一つの色が５個、他の色が２個の場合は
の mixing number を与えます。もちろん、直接検査してもカラーリングが unfriendly であることがわかります。
関数を使用して、20個の頂点と100個の辺を持つグラフ
を作成します。生成された辺のリストは次の通りです。
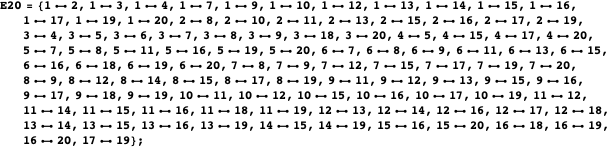
任意に、最初の10個の頂点を赤に、残りの10個を青に色付けします。
グラフのイメージと色付けは次の通りです。
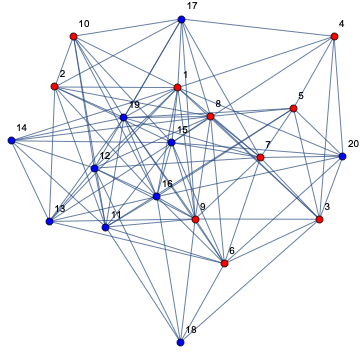
関数は、頂点の色を変更します。
例えば、これは頂点１を反転します。
グラフ内の頂点
の neighbors の集合、つまり、辺を共有するそれらの頂点を取得する必要があります。Mathematica に組み込まれている
関数には頂点自体が含まれているため、それを削除します。
にある頂点３の neighbors の例です。
次に、異なる色付けをされた頂点の辺を取得します。
そのリストの長さが辺
と色分割
の mixing number です。
が friendly neighborhood にある、つまり、は
にあるほとんどの neighbors と同じ色を持っている場合は、頂点をグラフのセキュアな頂点と呼びます。
関数
は、内のが色分割
でセキュアな頂点であるかどうかを判断します。
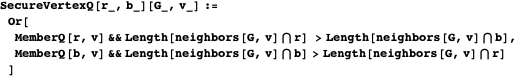
例えば、これらは
のセキュアな頂点です。
対応する関数
を定義します。
セキュアな頂点
のリスト内にある最初の要素を選択し、色をセットします。
の色を反転します。それはfriendly neighborhoodにあり、もしくは同等なので、セキュアな頂点です。
生成された色分割を使用してこの手順を繰り返し、セキュアな頂点がなくなったらやめることができます。次のセクションで、プロセスを最後まで実行し、最終的な色分割を出力する関数
を記述します。
次の短いプログラムは、色分割
で始まる２色グラフの unfriendly なカラーリングを生成します。
これはunfriendlyな色分割です。
これはunfriendlyなグラフのカラーリングです。
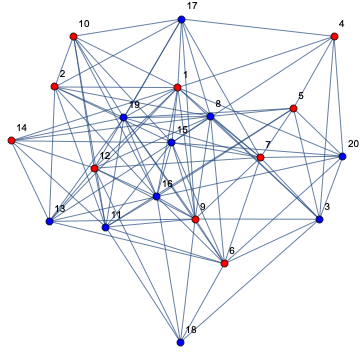
すべての頂点が同じ色の状態から始めることもできます。赤の場合、
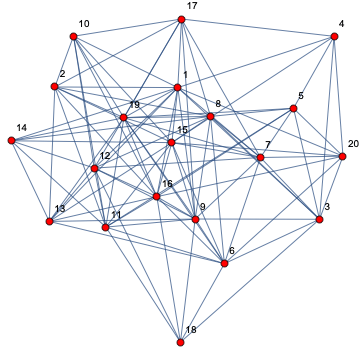
プログラムを実行し、新しい色分割を使用します。
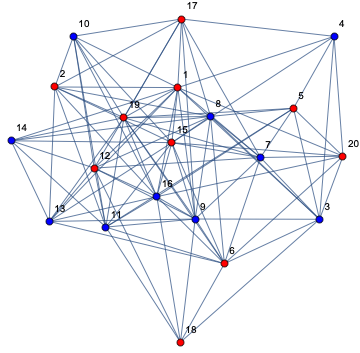
最大カット問題とは、グラフ
の頂点
を２つの集合
と
を２色でカラーリングすることと等しいです。最大カット問題はNP-hard［３、４］で知られています。それは、この最大値を見つける方法は、P＝NPでない限り、多項式時間で実行されないことを意味し、ほとんどの数学者はその可能性は低いと考えています。
最大カット問題のコンテキストでは、私たちの手順 
は局所探索法として知られており、グラフ［３］内の辺の数の少なくとも半分のカットを常に生成することを簡単に示すことができます。
私たちは、有限グラフのunfriendlyな２色を見つける方法を示しましたが、これはより多くの色に簡単に拡張することができます。頂点のカラーリングを頂点のリストの分割として扱い、これをグラフの不可欠で動的な部分と見なすことは、他のカラーリング問題を調査するのに役立つはずと我々は感じております。
最後に、この仕事を30年以上前に私と一緒にこの問題に取り組んだ Bill Emerson に捧げます（未発表の論文［１］の参考文献3参照）。Bili は非常に才能のある数学者であり、良き友人でした。 彼を知っているすべての人が彼を懐かしんでいます。
George Beck氏には論文中のプログラミングを改善していただき感謝します。Lenore Cowen教授には最大カット問題との関連性を指摘していただいたことに感謝します。
| [1] | R. Aharoni, E.C. Milner and K. Prikry, “Unfriendly Partitions of a Graph,” Journal of Combinatorial Theory, Series B, 50(1), 1990 pp. 1–10. https://doi.org/10.1016/0095-8956(90)90092-E. |
| [2] | S. Shelah and E. C. Milner, “Graphs with No Unfriendly Partitions,” A Tribute to Paul Erdős (A. Baker, B. Bollobás and A. Hajnal, eds.), Cambridge, UK: Cambridge University Press, 1990 pp. 373–384. |
| [3] | D. Panigrahi, “COMPSCI 638: Graph Algorithms, Lecture 22.” (Sep 10, 2021) https://courses.cs.duke.edu//fall19/compsci638/fall19_notes/lecture22.pdf. |
| [4] | M. R. Garey, D. S. Johnson and L. Stockmeyer, “Some Simplified NP-Complete Problems,” in Proceedings of the Sixth Annual ACM Symposium on Theory of Computing, New York: ACM, Seattle, WA, 1974 pp. 47–63. https://dl.acm.org/doi/10.1145/800119.803884. |
| R. Cowen, “Mixing Numbers and Unfriendly Colorings of Graphs,” The Mathematica Journal, 2021.doi.org/10.3888/tmj.23–4. | |
Robert Cowenは、ニューヨーク市立大学クイーンズ校の名誉教授です。彼の主な研究対象は論理と組合せ論です。彼は長年、Mathematicaを使って数学の研究をする方法を学生に楽しみながら指導しています。
Robert Cowen