| 本アーティクルは The Mathematica Journal (volume 18, 2016) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 18, 2016) and the copyright holder is Wolfram Research, Inc." |
の部分群に働く効率的なアルゴリズムについて説明します。
説明する操作は、join と meet、 共役テスト (congruence testing)、合同閉包 (congruence closure)、部分群テスト (subgroup testing)、カスプ列挙 (cusp enumeration)、スーパー群格子 (supergroup lattice)、生成元 (generators)、剰余類列挙 (coset enumeration)、生成元のリストから群を構築することです。
メビウス変換として知られる
 |
(1) |
の形式の一次分数変換の集合は、いくつかの興味深い特性をもっています。まず、この関数の成分は、次のように同じ形式のままです。
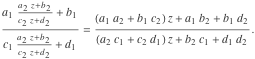
成分中にあらわれる係数は二つの行列 
と 
の積になっているため、行列 
で形式 (1) の変換を表現するのに便利です。
行列とその行列をゼロ以外の任意のスカラー倍したものは、同じメビウス変換を表すので、一般性を失うことなく行列式が 1 である行列のみを検討することができます。
行列式が 1 である二つの行列式の積もまた 1 であるため、その行列（もしくはメビウス変換）は群を形成し、その群の操作は行列乗算（もしくは成分）です。
もし、さらに (1) の係数 a, b, c, d を整数であると制限した場合、その結果の群は 
として知られます。
もし行列 が に存在するなら、
もまた に存在し、同じメビウス変換を表します。
そこで、各行列とその負の行列を同一とする であるようなモジュラー群として知られる について考えます。
モジュラー群のすべての変換は対応する行列 
と 
と、二つの基本的な変換の組み合わせ
として得られることを示すことができます。 この事実を述べる別の方法は、 を S と T から生成することです。
例えば、行列 
は積 TSTTST として得られます。
モジュラー関数の存在によりモジュラー群は重要です。モジュラー関数はモジュラー群の作用下でシンプルな変換法則を持つ関数です。プロトタイプモジュラー関数はモジュラー判別関数であり、 Im z>0 に対して、
で定義されます。
この積はすべての有理数でゼロを持つため、実軸は Δ(z) の領域 
の自然境界になります。 解析の方法を使って、モジュラー群のすべての行列 に対して、
 |
(2) |
を示すことができます。 変換式(2) について二つの観測が順番に行われます。まず、
について、z の変換された値が依然として正の虚部を持つことが分かり、それはまだ Δ(z) の領域にあります。
次に、上半平面 全体にわたる z の Δ(z) の値は、青色で影がつけられている領域で制限されるような z の Δ(z) の値に関係があります。
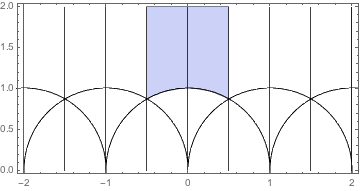
この領域は、 の基本領域として知られています。 これは変換 S と T が 内の任意の点をこの領域に持ってくるために使用することができ、 のメビウス変換によって、その内部の二つの点が異なることがないためです。 変換 T は左端と右端をペアにし、変換 S は i から e2π i/6 の弧と i から e2π i/3 の弧をペアにします。
モジュラー関数の理論では、どの変換が与えられた関数を変化させないかを知りたいときがあります。 例えば、
は、 のすべての要素の下で分子 Δ(5z) は変換式を持っていないため、 の変換によって変化することはありません。
しかし、もし が にあり、 c が 5 で割り切れるのであれば、
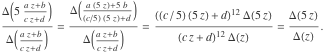
です。したがって
によって与えられる の部分群になります。
パッケージ ModularSubgroups.m は、そのようなモジュラー群の部分群で動く計算問題を扱います。 しかし、Γ0(5) の場合と同様に、 の特定の部分群のみがそのエントリの合同条件によって識別されます。 このような部分群は合同部分群と呼ばれ、後で詳しく論じます。この理由により、部分群を表現するのにより良い方法が必要です。この鍵は行列 S と O=T S にあります。 S と T は を生成するので、S と O もまた生成元です。 しかしながら、 は {I,S} と {I,O,O O} の自由積であることを示すことができます。すなわち、 のすべての行列は、ワードの中に連続する二つの S と連続する三つの O が現れない限り、 S と O のワードとして一意に書くことができます。この最後の条件は関係 S2=O3=±I のために必要で、 
(単位行列) は空のワードとして考えるべきです。
左剰余類 
が 
として定義され、 が左剰余類 の直和
として書けるのであれば、モジュラー群 の部分群 Γ は（ で）有限のインデックスを持つと言われます。この方法で、 は Γ のいくつかの"コピー"に分割され、 の中にフィットする Γ のコピーの数は、インデックス μ と呼ばれます。もし Γ が左剰余類 g1Γ,…,gμΓ (顕著な剰余類 g1Γ=Γ ) とインデックス μ であるような の有限インデックス部分群であれば、行列 S と O は左辺の乗算を行う際に、左剰余類を置換します。つまり、方程式
を持ち、ここで S と O は集合 {1,2,…,μ} のいくつかの置換、つまり対称群 Symμ の要素として見なされるべきです。
置換としての行列 S と O のこの識別は、 の任意の部分群を表すために使用される Γ の置換表現を生じさせます。具体的には、部分群 Γ は次によって識別されます。 (1) インデックス μ ; (2) 置換 S∈Symμ ; (3) 置換 O∈Symμ 。 置換 S と O は任意ではありません。 与えられた S,O∈Symμ がいくつかの群 Γ の表現として現れる必要十分条件は次の二つです。
を持っていることに起因します。
が剰余類 giΓ を剰余類 gjΓ へ送るので、左剰余類上の の動きを剰余類の全てと一緒に"接続"するため生じます。この二つの条件が満たされる場合、群 Γ は Γ={words w in S and O|w(1)=1} として識別されます。ここで条件 w(1)=1 は、 S と O をそれらの対応する置換に変換することによって w を置換として考えた後に評価される必要があります。
二つの置換 S と O による Γ の表現は、自明でない剰余類 g2Γ,…,gμΓ の任意の順序付けを必要とするので、S1 を S2 に、 O1 を O2 に同時に変換する Symμ の置換のインデックス 2,…,μ の再ラベリングがある場合、二つの異なる表現 (μ,S1,O1) と (μ,S2,O2) は正確に同じ群を表します。
例えば、二つの表現
は同じ群を表し、再ラベリング {2 → 2,3 → 4,4 → 3} は、 Γ1 を Γ2 に変換します。
有限インデックスの部分群 Γ に加えられた別の重要な組み合わせオブジェクトは、 [1] で説明されているように、Γ のためのファレイシンボルです。 このシンボルは基本領域のためのエッジペアリング行列と同様に、Γ のための基本領域を直接エンコードします。同じように、それは Γ のための独立した生成元をエンコードします。 しかし、二つの異なるファレイシンボルによる Γ の二つの表現の等価性は検出するのが簡単ではないため、記述された置換表現が Γ の基礎となる表現のために選ばれました。
いくつかの自然数 N に対して、
となるようなレベル N の主合同部分群を含む場合、 の部分群 Γ は合同部分群と呼ばれます。 この場合、Γ を要素が N を法として合同であることを満たす行列として記述することができます。 例えば、合同部分群の二つの集合は Γ0(N) と Γ1(N) であり、これらは次のように定義されます。
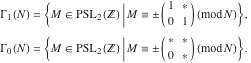
最近 [2] で Hsu は 
に対する表現に基づいて、与えられた の部分群が合同部分群であるかを判定するためのシンプルなテストを行いました。 このアルゴリズムを実装し、Γ を含む最小の合同部分群である部分群 Γ の合同閉包を計算するために一般化します。
Γ のシュライア剰余類グラフは、パッケージ内のアルゴリズムのいくつかにとって根本的に重要です。 部分群 Γ がインデックス μ と置換 S と O とともに与えられると、シュライア剰余類グラフは μ 個の頂点 1,…,μ と 2μ でラベル付けされた辺
を持つ接続グラフです。
このようなグラフは folded であるという特性を持っています。 もしすべての頂点が最大で 1つの与えられた向きとラベルの辺を持つならば、グラフは folded であると言います。もし、同じ向きとラベルの辺が二つ以上ある頂点があるならば、グラフは unfolded であると言います。 シュライア剰余類グラフの一つの特性は、モジュラー群の部分群 Γ が S と O のすべてのワード w で構成されており、頂点1 から始まるとき、ワード w に続くパスは、頂点1で終了しなければならないということです。例えば、次のシュライア剰余類グラフを持つ部分群 Γ を考えます。
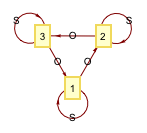
ワード w=O S O O 、対応する行列
は、
によって与えられる w によってパスがトレースされるため、Γ に存在します（左剰余類を扱っているので、w は右から左に読む必要があります）。 グラフは folded であるため、S と O のワードによって与えられるパスをトレースするプロセスは決定論的です。 このシュライア剰余類グラフに対応する群 Γ は合同部分群であることが分かり、その合同の定義は Example 1 に示されています。
これらの例はすべて Mathematica 10 でテストされています。
パッケージをロードできるようにディレクトリを設定し、Need を評価します。
モジュラー群の部分群はコンテナ mGroup[μ,S,O] に保持され、組み込みシンボルとの競合を避けるために、これらの群で動作する関数の名前は小文字の "m" で始まります。 パッケージの行列 mS, mO, mT, mR は次のように設定されます。
これはシュライア剰余類グラフのセクションの群 Γ です。置換は 
と 
となるようにリストされます。ここで S と O は mGroup コンテナの最後の二つの引数です。
この群はレベル 3 の合同部分群であることが分かり、以下の行列の１つに対して法 3 に関して合同であるような行列で構成されています。
したがって、例えば、群 Γ には、次の記述があります。
Tn と S によって生成された群は、n=±1,±2 に対してのみ有限インデックスです。
同様に、 Tn と O によって生成された群も n=±1,±2 に対してのみ有限インデックスです。
インデックス7 の合同部分群の二つの共役類があり、ここでは生成元を使ってそれらを定義します。 群 Γ のプリントされた形式は：
は で Γ のインデックスです。 
のジーナスです。
は Γ のカスプの数で, すなわち 
のサイズです。
は 
で Γ の位数2 の固定された点の数です。
は で Γ の位数3 の固定された点の数です。 これらの数は 
と関連しています。
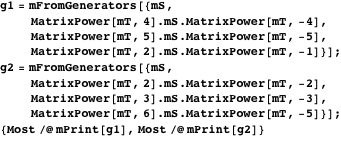
それらは共役ではありません。
これら二つの群の交点はインデックス 28 を持ち、これら二つの群によって生成された群は完全なモジュラー群になります。
基本領域は mDomain で取得できます。
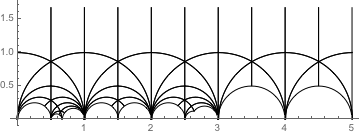
この基本領域の辺のペアは Farey シンボルで与えられます。同じ整数ラベル n を持つ二つの有理数間の辺 
は一緒にペアになっていて、ラベル ● か ○ のエッジはそれ自身とペアになっています。
mGenerators によって返される行列は、このようにして辺をペアにする行列です。
部分群 Γ の合同閉包は、Γ を含む最小合同部分群です。最初に、前の例のインデックス7 の合同部分群とインデックス9 の合同でない部分群から始めます。
その合同閉包はシータ部分群です。
群の合同閉包を同じレベルの主合同部分群と結びつけることで計算することもできますが、パッケージはより効率的な方法を使用します。群 Γ(N)、 Γ1(N)、と Γ0(N) の中のメンバーシップは、それぞれ mΓ[N]、mΓ1[N] と mΓ0[N] でテストすることができます。関数 mFromMember は、与えられたグループのメンバーシップ関数の内部的な表現を構築します。
g 自身は合同であるので、以下の特性を持ちます。
次に、[2] の Example 1.1 で与えられる群の合同閉包を計算します。 これは完全なモジュラー群であることが分かります。
まず、レベル5 の主合同部分群を取得します。これはインデックス60 を持っています。
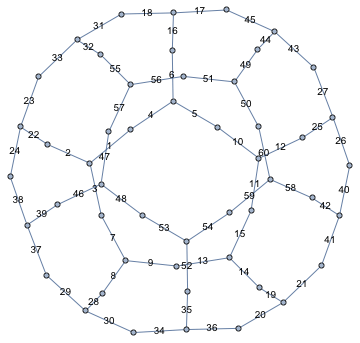
生成元はこの置換表現から素早く計算することができ、生成元のリストから群を効率的に再構成することもできます。
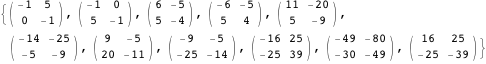
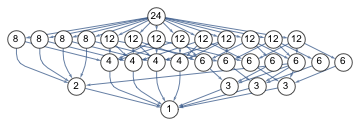
レベル4の主合同部分群のスーパー群格子をグラフ化します。
関数 mSupergroups はスーパー群格子を作るために使われます。( の) それぞれの群のインデックスが格子内に表示され、実際の群はツールチップとして表示されます。
4 を法とする合同条件で記述できる行列を持つ のすべての部分群が、この格子のどこかに現れます。
Γ がモジュラー群の部分群である場合、 Γ のすべての行列は 
(∞ を含む有理数の集合) 上で動作し、 を同値類に分割します。 ２つの有理数 x1 と x2 は、もし x1 から x2 へ送る Γ の要素がある場合、 Γ の下で同値であると言います。Γ の作用下で の同値類の集合は Γ のカスプとして知られ、モジュラー群内で Γ が有限インデックスを持つ場合、有限な多くのカスプが存在します。 Γ に対するカスプの幅は、x の スタビライザーの中の x の Γ スタビライザーのインデックスであるとして定義されます。
g と h を次の部分群とします。
次は h の同値なカスプのリストとその幅です。
ここでは、ランダムなカスプのリストを 4つのうちの 1つに減らします。リスト内のそれぞれのカスプの頻度は、その幅に比例する必要があります。
g と h の交点を計算することができます。
もちろん、パッケージの実装の方がより効率的です。
もし an がインデックス n のモジュラー群の部分群の総数を表すなら、
を 
とすると、
と、
であることを示すことができます。
べき級数 
の収束半径はゼロであるので、この微分方程式は形式的に f(x) の係数に対する漸化式として扱わなければなりません。 詳細は [3] の Section 1 を参照してください。
Caranica [4, Table 3.1] はインデックス9 の非合同部分群の共役類を計算しました。しかし、この表は 11 の共役類があると間違った主張をしています。 実際、インデックス 9 と 12 の共役類の非合同部分群は 108個あります。 Vidal [5] は与えられたインデックスの（合同もしくは非合同）部分群の共役類の数の生成関数の式を与えています。
12
幸いにも、主張された群の Farey シンボルは Caranica によって提供されているため、エラーの原因をリカバーすることができます。 まず、表に実際に非合同部分群の共役類が 11 あることを確認します。
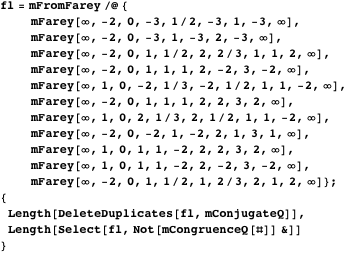
{11,11}
これは表から欠落している群です。
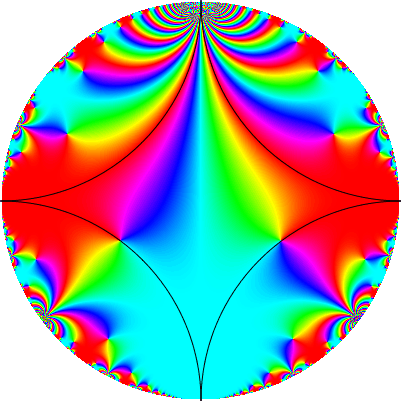
Mathematica の組み込み関数 KleinInvariantJ は の下で不変であり、 の基本領域中で、各複素数の値を正確に一度取ります。 この関数のプロットと基本領域の概要を示します。
z によってパラメータ化された上半平面は、 w=i (z-i)/(z+i) により、w=x+i y によってパラメータ化された単位円にマッピングされます。
w 円のある点にプロットされたカラーの色相は複素数 f(z) の引数であり、 z は w に対応する上半平面の点です。
同様に、組み込み関数 DedekindEta を使用して、インデックス3 の の合同部分群である Γ0(2) の関数 f(z) を構築することができます。この関数と Γ0(2) の基本領域のプロットを次に示します。
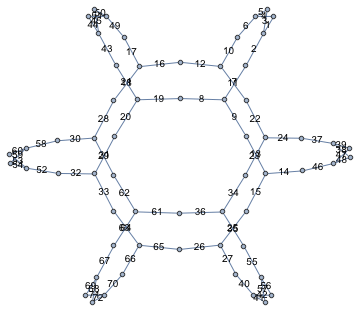
Γ(2) の場合も同様です。これは z 半平面に Γ(2) の基本領域をプロットします。
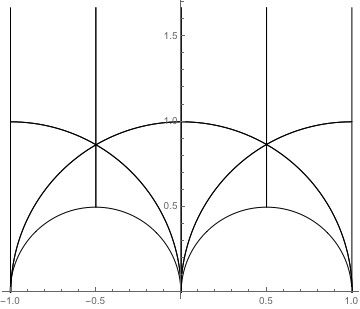
w 円では、このような領域は菱形になります。 
上の単葉関数は Γ(2) の生成元の下で不変です。言い換えると、
であり、このような関数は組み込み関数 ModularLambda によって与えられます。
この場合、 f(z) のゼロはこの菱形上で色が合体する場所で起こります。前の例では、 f(z) のゼロは w 円の境界上に存在するため見えません。
モジュラー群の部分群に対する多くの操作は、グラフの操作に依存します。ここで使用されているアルゴリズムのいくつかは、unfoldedグラフに遭遇します。グラフを foldedグラフに変換する Stallings の折り畳みプロセスの実装に、[6] で説明されている効率的な折り畳みアルゴリズムを使います。
導入で説明したように、置換 S と O によって記述された群 Γ をシュライア剰余類グラフに変換することは簡単です。 この手順を逆にするために、 O でラベル付けされた各辺は、同じ始点と終点を持つか、３サイクルの一部である必要があります。 同様に、 S でラベル付けされた各辺は、ループか、２サイクルで発生する必要があります。ここで使用されるグラフは全てこの特性を持っています。 しかし、生成元のリストから群を作成すると、いくつかの頂点が次数4 を持たない foldedグラフが発生することがあります。 このようなグラフは、有限インデックスの Γ の部分群に対応していません。次のグラフで折り畳み手順を説明します。
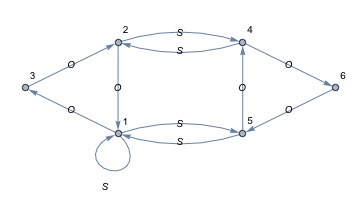
このようなグラフは、 S2=O3=1 の関係を含む自明なサイクルを除いて、グラフ中の唯一のサイクルであるため、二つのワード S と O S O S によって生成される Γ の部分群を表します。 同じ方向とラベルを持つ同じ頂点に二つの辺 v ↔ u と v ↔ w が存在するときはいつでも、グラフを unfolded にし、そのグラフによって表される部分群を変更することなく、辺 v ↔ w は削除され、頂点 w は u とマージすることができます。 グラフの折り畳み手順の進行は左から右へ、上から下へ示され、削除されるべき辺はグラフ間に示されます。
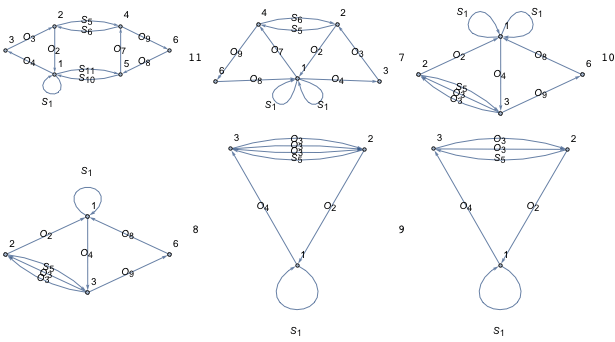
最後に折り畳まれたグラフによって表される の部分群はインデックス3 を持ち、
置換 S=(1)(23) と O=(132) によって決定されます。これはシータ部分群としても知られています。
S と O S O S O S によって生成された群の折り畳み手順を通して、 で有限のインデックスを持たないことを確認します。最初のグラフを次に示します。
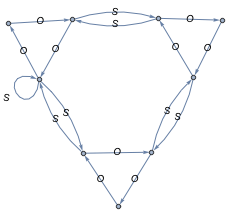
（置換 S と O の観点から）群 Γ の標準的な表現の概念を持つことは有用です。これにより、二つの群は S と O が同一である場合にのみ同じです。これは剰余類 Γ を最初に訪れること（置換のインデックス1 によって表される）によって達成することができます。剰余類 gi Γ を訪れたら、剰余類 Ogi Γ （これはまだ訪れていないと仮定します）を再帰的に訪れ、この旅が剰余類 gi Γ に戻ってきたら剰余類 Sgi Γ （これもまだ訪問していないと仮定します）を訪れます。自明でない剰余類のインデックス 2,…,μ のための標準ラベルは、その剰余類が訪問された順番によって決定されます。
行列 m が群 Γ のメンバーシップかをテストする場合、 m-1 を S と O のワードとして書き、r=1 を設定し、m-1(r)=1 であるかをチェックします。 具体的には、左の列のエントリが非負である与えられた行列 m∈ に対して、m の左側から行列
を左の列にゼロが入るまでかけます。変数 r は現在の剰余類を保持しているので、例えば、m を S O O で乗算する度に、r を S(O(O(r))) に更新する必要があります。
群の行列のメンバーシップ関数が与えられると、剰余類によって群剰余類を構築します。 で Γ が少なくともインデックスを三つ持っていると仮定します。 もし O∈Γ であるなら、4つの剰余類 L={Γ, S Γ, O S Γ, O O S Γ} で始めます。そうでなければ、三つの剰余類 L={Γ, O Γ, O O Γ} で始めます。 一度に１つもしくは３つの剰余類を L に加えることにより続行します。gi Γ∈L である場合：
これらの条件を満たす剰余類 gi Γ が存在しない場合、 Γ のすべての剰余類を発見しました。 この手順を素朴に実装すると最悪の場合の実行時間は O(μ3) になります。ここで μ は結果の群のインデックスです。 最悪の場合の実行時間は、どの剰余類を実際にチェックする必要があるかを追跡することにより、O(μ2) に減らすことができます。
インデックス μ の部分群 Γ に対する O(μ) 操作の剰余類表現、生成元、Farey シンボルを計算します。 これは次のように動作します。 G をインデックス μ の部分群に対応するグラフとします。 まず、i とラベル付けされた剰余類が頂点1 から頂点iまでの固有の経路の結果として与えられるようにグラフをツリーにカットします。 カットが行われるか、固定された点に遭遇すると、対応する行列が生成元のリストに追加されます。 最後に剰余類と生成元が計算されカットが記録された後、Fareyシンボルをツリーの時計回りの走査によって計算します。
与えられた部分群 Γ のカスプも重要です。 左半平面上の の操作は、
によって与えられ、この操作は 
に拡張されます。Γ の作用下での 
の同値類、すなわち /Γ は有限で、次のようにそれぞれの表現を選ぶことができます。 で ∞ のスタビライザーは O S (or T) によって生成されます。したがって、二つのカスプ（ 
に対して 
と 
）は、
であるような整数 n があるときは常に同値です。すなわち、m1Γ と m2Γ は、同じ置換 O S のサイクルに属しています。 カスプ の幅は、剰余類 m1Γ を含む ( O S の) サイクルの長さとして定義できます。
二つの群に属し、交差することは驚くほど簡単です。 Γ1 と Γ2 によって生成された群を計算するために、 Γ1 のグラフ G を作成します。 次に、Γ2 の各生成元 g に対して剰余類 Γ1 と g Γ1 に対応する G の頂点をマージします。 これは一般に unfolded のグラフをもたらし、これを fold して置換表現に戻すことができます。 Γ1 と Γ2 の交点の置換表現を計算するには、まず形式 m1 Γ1⋂m2 Γ2 の剰余類の観点から S と O の作用下の Γ1⋂Γ2 の軌道を求めます。 Γ1⋂Γ2 の置換表現は、この Γ1⋂Γ2 の軌道の剰余類上の S と O の作用によって得られます。
二つの群が同じか共役であるか、ある群が別の群に含まれているかどうかを確認することも簡単です。二つの群 Γ1 と Γ2 が同じかどうかをテストするために、表現を標準化する手順と同様の戦略を採用します。剰余類 Γ1 と Γ2 は同時に訪れ、ペア (Γ1, Γ2)から開始します。 もし現在ペア (m1 Γ1,m2 Γ2) を訪れているならば、標準化手順で説明したように (O m1 Γ1,O m2 Γ2) と (S m1 Γ1,S m2 Γ2) に訪れます。もし、二つの経路が同期しない、つまり、剰余類が別の順番で訪問された場合、群は同じでないことが分かります。そうでなければ、二つの経路は (Γ1,Γ2) に戻り、 Γ1 と Γ2 が同じであることが分かります。同じ手順で Γ1 と Γ2 が共役であるかを確認することができます。
のいくつかのペア (gΓ1,Γ2) から始めるとき、経路が同期しているかを確認する必要があります。
合同関数は Hsu [2] の関係のリストを使います。群 Γ の合同閉包 Γc は、 Γ を含む最小合同部分群であることを思い出してください。次のような Γ の合同閉包を計算します。Hsu は Γ が合同部分群である場合のみ満たされる関係 x = y のリストを与えます。L を置換 xy-1 のリストとし、 x = y が Hsu のリストの関係であるとします。もし L が非同一置換 p を含んでいるならば、これは Γ が合同部分群であることへの障害を表します。N を置換 O S の次数として定義される Γ のレベルとします。 Γc は Γ(N) を含むことが知られているので、 Γ の関係の集合もまた Γc を満たします。p を L の任意の置換であるとし、 i を Γ の任意の剰余類のインデックスとします。 p は Γc の剰余類上で自明に動かなければならず、 Γ は Γc の部分群であるため、 剰余類 i と p(i) をマージすることによって Γ から得られる群もまた Γc に含まれなければなりません。したがって、全ての p と i に対して Γ の剰余類 i と p(i) をマージすることは Γc を与えなければなりません。
モジュラー群の部分群を操作および構築するための効率的なパッケージについて説明しました。これが、これらの群にさらなる関心を起こし、この部分群を扱う研究を促進することに期待します。
著者はイリノイ大学アーバナ・シャンペーン校の Junxian Li による、アルゴリズムの初期の実装への改善と修正に関する多くの有益な議論に感謝します。
| [1] | C. A. Kurth and L. Long, “Computations with Finite Index Subgroups of Using Farey Symbols.” arxiv.org/abs/0710.1835. |
| [2] | T. Hsu, “Identifying Congruence Subgroups of the Modular Group,” Proceedings of the American Mathematical Society, 124(5), 1996 pp. 1351–1359. www.ams.org/journals/ proc/1996-124-05/S0002-9939-96-03496-X/S0002-9939-96-03496-X.pdf. |
| [3] | A. Lubotzky, “Counting Finite Index Subgroups,” London Mathematical Society Lecture Note Series 212: Groups ’93 Galway/St Andrews, Vol. 2 (C. M. Campbell, E. F. Robertson, T. C. Hurley, S. J. Tobin, and J. J. Ward, eds.), Cambridge: Cambridge University Press, 1995 pp. 368–404. |
| [4] | C. C. Caranica, “Algorithms Related to Subgroups of the Modular Group,” Ph.D. thesis, Louisiana State University, 2009. etd.lsu.edu/docs/available/etd-07092009-200839/unrestricted/Caranica_diss.pdf. |
| [5] | S. A. Vidal, “Sur la classification et le dénombrement des sous-groupes du groupe modulaire et de leurs classes de conjugaison,” Publications IRMA, 66(II), 2006 pp. 1–35. Preprint: arxiv.org/abs/math.CO/0702223. |
| [6] | N. W. M. Touikant, “A Fast Algorithm for Stallings’ Folding Process,” International Journal of Algebra and Computation, 16(6), 2006 pp. 1031–1045. doi:10.1142/S0218196706003396. |
| D. Schultz, “Manipulating Subgroups of the Modular Group,” The Mathematica Journal, 2016. dx.doi.org/doi:10.3888/tmj.18-4. | |
Daniel Schultz はペンシルベニア州立大学のポストドクター研究員であり、一般にモジュラー関数と保型形式に興味があります。
Daniel Schultz