| 本アーティクルは The Mathematica Journal (volume 19, 2017) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| “This article was previously published in The Mathematica Journal (volume 19, 2017) and the copyright holder is Wolfram Research, Inc.” |
Input Shapingは、柔軟な機械システムが最小の残留振動で動作するようにプレフィルタを生成する、確立された技術です。 例えば宇宙構造物、ロボット、クレーンなどの工学的システムに多くの例がみられます。振動制御は、構造的な柔軟性の存在下で精密な運動が要求される場合には深刻な問題たり得ます。例えば風力発電用のタービンブレードでは、フラップ方向の振動を処理しなければブレードの寿命は縮まり、予想外の振動が土台の支持構造体にまで広がる可能性があります。このアーティクルでは、Input Shaping技術を使用して柔軟な機械システムが内包する振動を制御できるツールについて検討します。
フレキシブルシステムの振動を低減するための選択肢[ 1、2 ]の中で、Input Shaping制御は、一連のインパルスを必要な畳み込み(convolving)で抑制することで実現される開ループ制御技術です。 インパルスの振幅と時間位置は、一連の制約式を解くことでシステムの固有振動数と減衰比から決定されます。 歴史をひもとけば、Input Shaping は1950年代後半に端を発します。もともとは” Posicast Control “と呼ばれていましたが、Input Shapingの研究初期の功績は、主にSmith [ 3、4 ]と、CalvertとGimpel [ 5 ] によるものでした。 これら3つの研究はいずれも、ステップ入力を受けて軽度に減衰された、システムからの非振動応答を生成する簡素な手法を提案するもので、減衰しきれなかったシステムの振動運動を、単純な波の相殺の概念で抑制しようとするものでした。 初期の形式のコマンドジェネレータは、固有振動数と減衰比のモデル化の誤差に敏感であるため、ロバスト性が低いという問題がありました。 この初期の研究以来、Input Shaping制御の分野では多くの開発が行われ、ペーシング要素のなかには、この概念を実装するためのマイクロプロセッサ技術の進歩といえるものもありました。 例えば、Swigert [ 6 ]による、モデルパラメータの種類に終端状態の感度を考慮したトルクプロファイルの決定手法の研究などは、より最近のロバストなコマンドジェネレータが実システムに有益であることを証明しています。他に、ZVD(Zero Vibration and Derivative)シェーパと初期に呼ばれていた、 固有振動数モデリング誤差に対してロバストな入力シェーパの他の例が開発されていますが、残留振動の大きさの微分に追加の制約を加えることで、モデリング誤差に対するロバスト性が改善されました。この改善で、クレーンの移動[ 8,9 ]、ディスクドライブの正確な移動[ 10 ]、柔軟性をもった宇宙船[ 11,12 ]、産業用ロボット[ 13,14]座標測定機[ 15 ]など多様なシステムへの実装が進みました。他にもハイブリッドInput Shaping[ 16 ]と3ステップInput Shaping技術[ 17 ]を用いた開発も行われています。
フレキシブルなダイナミクスの問題には、フィードバック制御、コマンドシェーピング、物理的なジオメトリの再設計など、さまざまなソリューションが考えられます[ 18 ]。 この難易度の高い領域の比較的簡単な例は、オーバーヘッドガントリークレーン(走行型架台式クレーン)の単純な例で、図1に示すように、長さ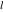 分の非伸張性ロープ(ケーブル)と、質点
分の非伸張性ロープ(ケーブル)と、質点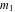 の運搬物(ペイロード)を伴った質点
の運搬物(ペイロード)を伴った質点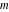 の可動構造部(crab/crane)からなっています。
の可動構造部(crab/crane)からなっています。
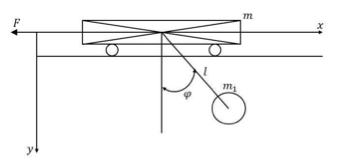
図1.オーバーヘッドガントリークレーンの概略図
このようなシステムの運動方程式は、ニュートン力学から直接的に、またはラグランジアン法を用いて間接的に設定することができます。 どちらを使用しても、運動の非線形方程式系は次のようになります。
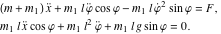 |
(1) |
ガントリークレーンが加速または減速しているとき、ケーブルは振動を始めます。図2にある方程式( 1 )のコードが示すように、力 が正に設定され、特にクレーンが加速しているときにケーブルの動きが顕著になります。 減速の結果は、コード中の
が正に設定され、特にクレーンが加速しているときにケーブルの動きが顕著になります。 減速の結果は、コード中の の
の に、単に負の値をわりあてればわかります。
に、単に負の値をわりあてればわかります。

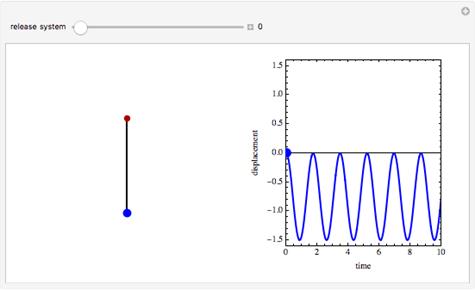
図2.加速時のオーバーヘッドガントリークレーン
特殊なケースは、ガントリークレーンが一定の速度で動いている、すなわち、 がゼロになっている場合です。 すると、垂れ下がっているケーブルが揺れないので、図3のようにクレーンと振り子が動きます。
がゼロになっている場合です。 すると、垂れ下がっているケーブルが揺れないので、図3のようにクレーンと振り子が動きます。

図3.一定速度で移動する時のオーバーヘッドガントリークレーン
ケーブルの上端は、運搬物を位置決めするためにレールに沿って移動するトロリー(クレーン上を走る移動式滑車)に取り付けられています。 クレーンは通常、レバーを動かすかボタンを押してトロリーを動かす人員(オペレータ)により制御されます。 オペレータが制御ボタンを一定の時間押せば、トロリーは一定の距離を移動して休止します。 ですが運搬物は通常、図3に示すように、制御されていない振動が、トロリーの動きによってトロリー上にある程度の振動を起こしてしまいます。 オペレータは、このボタンを適切に何度か押して、この状況を滑らかにします。このシナリオ下での運搬物の挙動は、図4に示すように、 「オペレータ制御」とします。

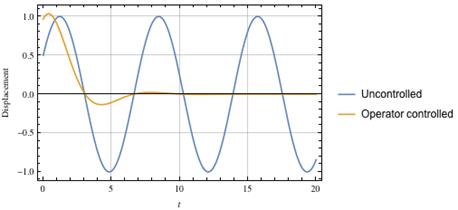
図4.制御されていないオペレータ制御の運搬物応答
ここでは、振動なしにシステムを動かす最も簡単なコマンドから始めます。 システムに加えられるインパルスは通常、それを振動させますが、第2のインパルスでキャンセルされ得ます。 この概念は図5に示されており、各入力は区分的に一定であり、純粋に減衰のない振動的システムが考慮されています。 ご欄のとおり、応答関数は合計してゼロを与えます。

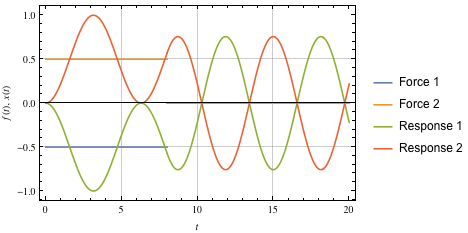
図5.単純な振動のキャンセル
次に、図6は、2つのインパルスコマンドに対する典型的な減衰強制システムの応答を示しています。
図6.一般的なバネ減衰システム
上記のシステムでは、運動方程式は次のようになります。
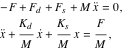 |
(2) |
ここで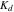 そして
そして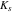 はそれぞれ、抗力、およびばね剛性による係数です。 ここでも、各入力は区分的に一定ですが、運動方程式には運動速度に応じた追加の減衰項があります。 なお、図7に示された2つのインパルスコマンドの振幅と時間位置を導出すると様々なことがわかります。
はそれぞれ、抗力、およびばね剛性による係数です。 ここでも、各入力は区分的に一定ですが、運動方程式には運動速度に応じた追加の減衰項があります。 なお、図7に示された2つのインパルスコマンドの振幅と時間位置を導出すると様々なことがわかります。

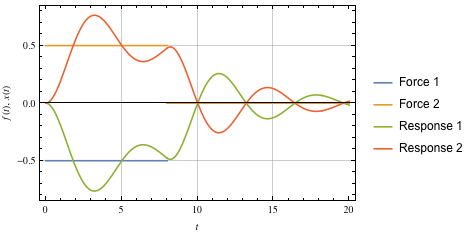
図7.減衰を伴う2つのインパルス応答
システムの固有振動数の妥当な推定値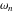 と減衰比
と減衰比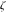 が判明している場合、一連のインパルスから生じる残留振動は、式( 10 )で表せます。
が判明している場合、一連のインパルスから生じる残留振動は、式( 10 )で表せます。
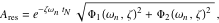 |
(3) |
ここで
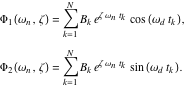 |
(4) |
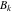 および
および 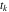 はインパルスの振幅と時間位置であり、
はインパルスの振幅と時間位置であり、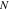 はインパルス系列におけるインパルスの数で、
はインパルス系列におけるインパルスの数で、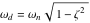 です 。
です 。
式( 3 )は、実際に単位強度の単一インパルスで引き起こされる振動に関連して生じる、一連のインパルスが引き起こす振動量の尺度である残留振動のパーセンテージです。 方程式( 3 )をゼロとして自明な解を避け、残留振動がゼロになるインパルス振幅および時間位置の値を見つけることができます。 値ゼロの自明な解を避けて正規化された結果を得るためには、インパルスは1に合算する必要があります。
すなわち、
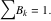 |
(5) |
しかし、インパルスは、正と負の両方の非常に大きな数を取ることによって、方程式( 5 )を満たすことができます。 これを軽減するために、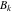 の値を正の値に制限する有限解を課します。
の値を正の値に制限する有限解を課します。
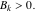 |
(6) |
2つのインパルスシーケンスにおいては 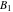 、
、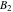 、
、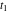 、
、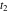 の4つの未知数があります。 一般性を失うことなく、最初のインパルスの時間位置をゼロに等しく設定できます。 式( 3 )を満たすために、式( 4 )の式は両方ともゼロに等しくなければなりません。 したがって以下のことがいえます。
の4つの未知数があります。 一般性を失うことなく、最初のインパルスの時間位置をゼロに等しく設定できます。 式( 3 )を満たすために、式( 4 )の式は両方ともゼロに等しくなければなりません。 したがって以下のことがいえます。
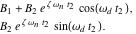 |
(7) |
これら2つの式のうちの2番目の式は、正弦項をゼロに設定することによって、非自明的に満たすことができます。これは以下の場合にみられます。
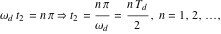 |
(8) |
ここで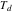 は振動の減衰時間をさします。 これは、もちろん、第2のインパルスの位置には無数の可能な値が存在するが、最短時間で振動を打ち消すために、
は振動の減衰時間をさします。 これは、もちろん、第2のインパルスの位置には無数の可能な値が存在するが、最短時間で振動を打ち消すために、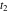 が選択されます:
が選択されます:
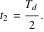 |
(9) |
この場合、式( 5 )で与えられる振幅制限は、
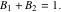 |
(10) |
となり、減衰された固有振動数の式を用いて方程式( 9 )および( 10 )を方程式( 5 )の第1の式に代入すると、
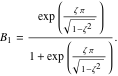 |
(11) |
となり、残留振動がゼロになる2つのインパルスのシーケンスは、次のように要約できます。
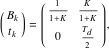 |
(12) |
ここで 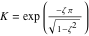 です。
です。
既に述べましたようにゼロ振動(ZV)入力シェーパが有用なのは、システムのパラメータが高度に正確であることが分かっている状況が前提です。 また、Input Shapingアプローチの信頼性や実績がほとんどない場合も、アプリケーションはシェーピング前のレベルを超えて振動を増加させません[ 19 ]。 [ 20 ]以前の入力成形に関する記事では、方法を使用する際の概念的説明が一般的に受け入れられたとしても、固有振動数の問題が混乱していることが指摘されています。Kang [ 20 ]は  システムの減衰されていない固有振動数の実際の値である変数(変数)と、
システムの減衰されていない固有振動数の実際の値である変数(変数)と、  (定数)、減衰されていない固有振動数の「モデル化」された値
(定数)、減衰されていない固有振動数の「モデル化」された値 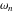 を区別しました。 Kang [ 20 ]はまた、振動がゼロに近づくことを証明しています
を区別しました。 Kang [ 20 ]はまた、振動がゼロに近づくことを証明しています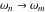 。この記事では、 振動システムの場合、モデリングの周波数は、モデリング周波数
。この記事では、 振動システムの場合、モデリングの周波数は、モデリング周波数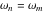 において
において 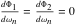 であるように選択されています。 次のコードは、残留振動の振幅をシステムパラメータの関数としてプロットすることによって、ZVシェーパの感度曲線(図8)を生成します。この場合、モデリング角振動数は
であるように選択されています。 次のコードは、残留振動の振幅をシステムパラメータの関数としてプロットすることによって、ZVシェーパの感度曲線(図8)を生成します。この場合、モデリング角振動数は 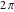 rad / sであり、減衰比は0.0です。
rad / sであり、減衰比は0.0です。

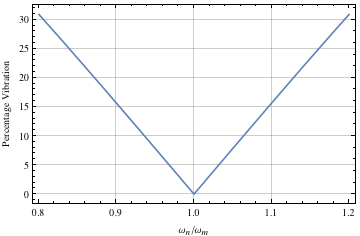
図8.ZV入力シェーパの感度曲線
インパルスの振幅および時間位置は、システムパラメータ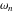 や
や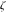 に依存します 。 これらの値に誤差がある場合(常にある場合[ 18 ])、インパルスシーケンスはゼロ振動になりません。 ZVD(Zero Vibration and Derivative)シェーパは、Input Shapingプロセスをこれらのモデリングエラーに対してよりロバストにするために設計されたコマンド生成スキームです。 モデル化誤差に対するロバスト性を高めるために、ZVD入力シェーパは2つの導関数を[ 20 ] 制約として加えます。
に依存します 。 これらの値に誤差がある場合(常にある場合[ 18 ])、インパルスシーケンスはゼロ振動になりません。 ZVD(Zero Vibration and Derivative)シェーパは、Input Shapingプロセスをこれらのモデリングエラーに対してよりロバストにするために設計されたコマンド生成スキームです。 モデル化誤差に対するロバスト性を高めるために、ZVD入力シェーパは2つの導関数を[ 20 ] 制約として加えます。
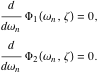 |
(13) |
ZVDシェーパのシーケンスは次のように要約できます。
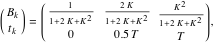 |
(14) |
ここで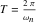 です。
です。
ZVシェーパの代替案は、図9に示すように、ZVシェーパよりもはるかにロバストなZVDシェーパです。しかし、ZVDシェーパは、ZVシェーパの半周期長とは対照的に、振動周波数の1周期に等しい持続時間を有します。このトレードオフは入力シェーパの設計プロセスにはつきものなので、通常は入力シェーパの長さを増やす必要があります。 ZVDよりも敏感でない入力シェーパは、0に等しい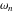 に関する方程式の二次導関数(3)を設定して得ることができます。 これはZVDDシェーパと呼ばれます。 このアルゴリズムは、式( 3 )を繰り返し微分することで無期限に拡張することができます。 減衰システム用のZV、ZVDおよびZVDDシェーパの閉形式解が存在します[ 7 ]。 敏感でない制約を使用して感度を下げるための代替手順が導出されています[ 21 ]。 モデリング周波数で残留振動をゼロにする代わりに、残留振動は低いレベルの
に関する方程式の二次導関数(3)を設定して得ることができます。 これはZVDDシェーパと呼ばれます。 このアルゴリズムは、式( 3 )を繰り返し微分することで無期限に拡張することができます。 減衰システム用のZV、ZVDおよびZVDDシェーパの閉形式解が存在します[ 7 ]。 敏感でない制約を使用して感度を下げるための代替手順が導出されています[ 21 ]。 モデリング周波数で残留振動をゼロにする代わりに、残留振動は低いレベルの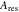 に制限されます。 感度カーブのノッチの幅は、モデリング周波数より低い周波数と、高い周波数の2つの周波数で振動を強制的に0にすることによって最大化されます。
に制限されます。 感度カーブのノッチの幅は、モデリング周波数より低い周波数と、高い周波数の2つの周波数で振動を強制的に0にすることによって最大化されます。
図9は、2つの内部最大値、振動数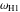 と
と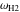 、これは式( 15 )で定義されているように、振動は
、これは式( 15 )で定義されているように、振動は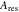 と等しくなければならず、またその導関数はゼロに等しくなければならないことを示しています。
と等しくなければならず、またその導関数はゼロに等しくなければならないことを示しています。
これらの制約は、以下のようによみかえられ、
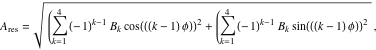 |
(15) |
そして
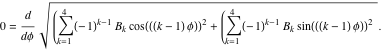 |
(16) |
となります。ここで 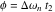 と
と 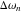 は、
は、 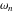 と
と 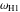 の間の差を示しています。 注意していただきたいのは 、
の間の差を示しています。 注意していただきたいのは 、 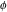 はモデリング振動数から感度曲線の最初の山に対応する振動数へのシフトを表しています。
はモデリング振動数から感度曲線の最初の山に対応する振動数へのシフトを表しています。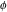 は
は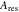 に依存し、最終的なシェーパの式には現れません。 他の条件は、インパルス振幅が1に合わなければならず、シェーパが感度カーブを形成するために1周期半の持続時間を有する4つの等間隔のインパルスを含むという仮定に沿うことです[ 21 ]。そこで
に依存し、最終的なシェーパの式には現れません。 他の条件は、インパルス振幅が1に合わなければならず、シェーパが感度カーブを形成するために1周期半の持続時間を有する4つの等間隔のインパルスを含むという仮定に沿うことです[ 21 ]。そこで
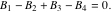 |
(17) |
これらの条件を使用して次のようになり、
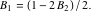 |
(18) |
方程式( 15 )および( 16 )を展開し、項を結合し、方程式( 18 )を使用して次のようになり、
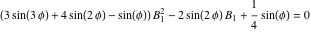 |
(19) |
そして
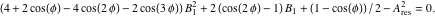 |
(20) |
式( 19 )は、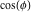 について解かれ:
について解かれ:
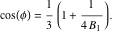 |
(21) |
式( 21 )を式( 20 )に代入すると、
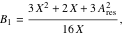 |
(22) |
ここで
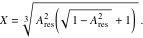
減衰していないシステムの2つの塊状のシェーパは、次のようにまとめられます。
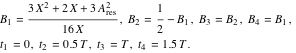 |
(23) |
次のコードは、上記の解析に基づいて2つの塊状のシェーパを生成し、それをZVDシェーパと比較します。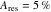 のとき、モデリング誤差(すなわち、感度曲線の幅)に対する不感受性は100%以上増加します。 ここでも、モデリング周波数
のとき、モデリング誤差(すなわち、感度曲線の幅)に対する不感受性は100%以上増加します。 ここでも、モデリング周波数 は
は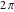 rad / sで設定されています。
rad / sで設定されています。

図9.感度曲線
ロバスト性は振動数の誤差に限定されません。 図10は、0と0.1との間の減衰比の範囲にわたって振動を抑制するように設計されたシェーパの3次元感度曲線を示しています。

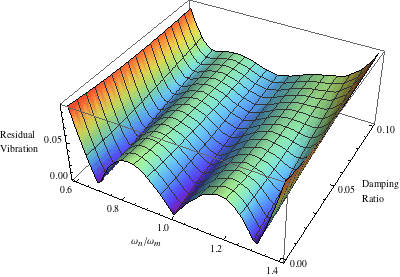
図10.減衰比による変化を含む3次元曲線
減衰型振動ダイナミックシステムモデルは、伝達関数
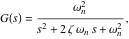 |
(24) |
でしめされます。ここで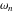 そして
そして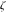 は再び固有振動数と減衰比です。 図11は、減衰係数に応じたさまざまな応答を示しています。
は再び固有振動数と減衰比です。 図11は、減衰係数に応じたさまざまな応答を示しています。

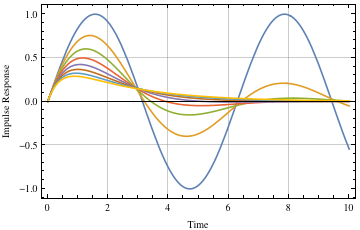
図11.異なる減衰係数の入力に対する応答
図11に示す応答の式は、次のとおりです。
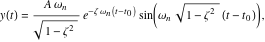 |
(25) |
ここで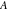 と
と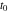 はそれぞれインパルスの振幅および時間です。 さらに、一連のインパルスに対する応答は、重ね合わせ原理を用いて得ることができます。 したがって、
はそれぞれインパルスの振幅および時間です。 さらに、一連のインパルスに対する応答は、重ね合わせ原理を用いて得ることができます。 したがって、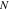 インパルス応答は、
インパルス応答は、 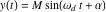 のように表すことができます。ここで
のように表すことができます。ここで
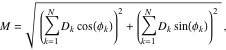 |
(26) |
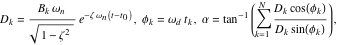 |
(27) |
ここで 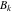 と
と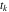 は はやはり、インパルスが発生する大きさと時間です。
は はやはり、インパルスが発生する大きさと時間です。
モデルが完璧でない場合の応答への影響を実証するために、ロバストな4インパルスZVDDシェーパを使用して次のコードを記述しました。 図12は、成形が行われない場合、モデルが完璧な場合、および周波数推定値に20%の誤差がある場合の応答を示しています。 入力シェーパが適用されていない場合、初期ピーク応答は57%にカットされます。

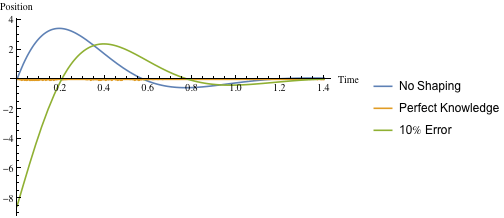
図12.モデルが完璧でない場合の対応
風車の羽根の振動は、羽根の寿命を短くし、振動を支持塔に伝達させ、柔軟でない構造を振動させるので、深刻な問題です。 振動振幅の増加の1つの原因は、ピッチ角入力の変化です。 ここでは、ZV入力シェーパを使用して、ピッチ角が大きいときから小さいときに振幅の減少を実証します。 風車翼の振動を抑制する方法は数多く開発されていますが、ピッチ角を急激に変化させた場合の振動の影響を抑制する方法に関してはあまり研究されていません。 急激に変化するピッチ角入力はステップ入力とみなされ、ブレードにいくらかの追加の振動(より大きな振幅)を引き起こします。 この例では、入力シェーパを使用してブレード角度の偏向を低減する効果が調査されています。 ここでは、ハブの末端部を固定し、他の末端を自由に動かす片持ち梁として風車羽根を検討します。 回転の影響は遠心強化を含めることによって考慮され、モーダル形状はAdomian修正分解法[ 22 ]を用いて計算されました。 ピッチ角を変化させる効果を組み込むために、よく知られたブレード要素理論[ 23 ]を用いて、ピッチ角の関数として揚力および抗力の成分からなる一般化垂直力を形成しました。 次に、運動エネルギー、ポテンシャルエネルギーおよび空気力学的力の表現を用いて、ブレードフラップ方向のたわみの動きを支配するブレードのラグランジアン(ラグランジュ関数)を形成しました。
図13は要約されたスキームでZV入力シェーパが使用された、予期しない風の外乱を扱うInput Shaping制御スキームのブロック図になります。
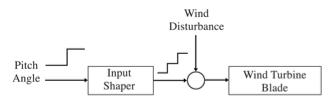
図13.入力シェーパコントローラの概略図
Input Shaping制御はフィードフォワード制御方法であり、整形入力のみがシステムを制御するために使用されます。 着眼点は、ブレードのフラップ方向のたわみがどのようにピッチ角の変化に反応するかを見ることです。 ピッチ角は、最初に4度の迎え角で設定されます。 図14は、定常状態に達したときのピッチ角が4度のフラップ方向の偏向を示し、図15は14度の偏向を示します。 より小さい角度でブレードのたわみが悪化していることが分かります。これは、風車ブレードが pitch-to-feather タイプ(低風速時は迎え角を大きくしてより多くの風を受け、定格風速以上の際は羽根の角度を小さくして、余分な風を通過させる)なためです。
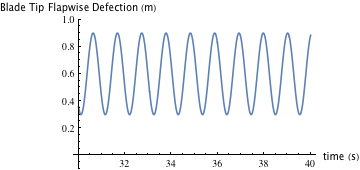
図14.フラップ方向のたわみ(ピッチ角4度)
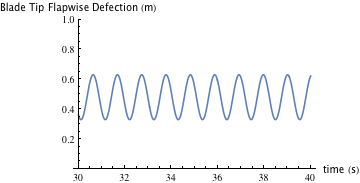
図15.フラップ方向のたわみ(ピッチ角14度)
ピッチ角がフラップ方向のたわみにどのように影響するかを見るために、ピッチ角を30秒で14 度から4 度に変更します。 図16は、ピッチ角が14度に設定されたときと30秒後のたわみが異なるため、若干の残留振動が発生することを示しています(青色の曲線)。 これは、モデルでは最初に減衰がないためです。 次に、入力シェーパが追加され、明らかに図16の破線のオレンジの曲線から、残留振動が低減されます。
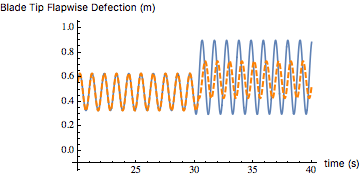
図16.ピッチ角変更の効果
Input Shapingに使用できるツールのいくつかを今回調査しました。ここでは、与えられたシステムへの入力が残留振動を最小限に抑えるよう、作成されています。 これらの技術が将来使用されるにあたって重要なことは、システムパラメータ内でエラーを許容することができ、ロバストであることが示されていることです。 すなわち、シェーパによって残留振動はゼロにならない場合もありますが、一般的には振動が大きく減少するといえます。
| [1] | J.-H. Park and S. Rhim, “Experiments of Optimal Delay Extraction Algorithm Using Adaptive Time-Delay Filter for Improved Vibration Suppression,” Journal of Mechanical Science and Technology, 23(4), 2009 pp. 997–1000.doi:10.1007/s12206-009-0328-1. |
| [2] | Q. H. Ngo, K.-S. Hong and I. H. Jung, “Adaptive Control of an Axially Moving System,” Journal of Mechanical Science and Technology, 23(11), 2009 pp. 3071–3078.doi:10.1007/s12206-009-0912-4. |
| [3] | O. J. M. Smith, Feedback Control Systems, New York: McGraw-Hill Book Company, 1958. |
| [4] | O. J. M. Smith, “Posicast Control of Damped Oscillatory Systems,” Proceedings of the IRE, 45(9), 1957 pp. 1249–1255.doi:10.1109/JRPROC.1957.278530. |
| [5] | D. J. Grimpel and J. F. Calvert, “Signal Component Control,” Transactions of the American Institute of Electrical Engineers , 71(5), 1952 pp. 339–343.doi:10.1109/10.1109/TAI.1952.6371288. |
| [6] | C. J. Swigert, “Shaped Torque Techniques,” Journal of Guidance, Control, and Dynamics, 3(5), 1980 pp. 460–467. doi:10.2514/3.56021. |
| [7] | N. C. Singer and W. P. Seering, “Preshaping Command Inputs to Reduce System Vibration,” Journal of Dynamic Systems, Measurement, and Control, 112(1), 1990 pp. 76–82. doi:10.1115/1.2894142. |
| [8] | K. L. Sorensen, W. E. Singhose and S. Dickerson, “A Controller Enabling Precise Positioning and Sway Reduction in Bridge and Gantry Cranes,” Control Engineering Practice, 15(7), 2007 pp. 825–837. doi:10.1016/j.conengprac.2006.03.005. |
| [9] | M. A. Ahmad, R. M. T. R. Ismail, M. S. Ramli, R. E. Samin and M. A. Zawawi, “Robust Input Shaping for Anti-Sway Control of Rotary Crane,” Proceedings of TENCON 2009—IEEE Region 10 Conference, Singapore, Jan. 23–26, 2009 pp. 1039–1043. doi:10.1109/TENCON.2009.5395891. |
| [10] | W. E. Singhose, W. Seering and N. C. Singer, “Time-Optimal Negative Input Shapers,” Journal of Dynamic Systems, Measurement, and Control , 119(2), 1997 pp. 198–205. doi:10.1115/1.2801233. |
| [11] | D. Gorinevsky and G. Vukovich, “Nonlinear Input Shaping Control of Flexible Spacecraft Reorientation Maneuver,” Journal of Guidance, Control, and Dynamics , 21(2), 1998 pp. 264–270. doi:10.2514/2.4252. |
| [12] | L. Y. Pao and W. E. Singhose, “Verifying Robust Time-Optimal Commands for Multimode Flexible Spacecraft,” Journal of Guidance, Control, and Dynamics, 20(4), 1997 pp. 831–833. doi:10.2514/2.4123. |
| [13] | J. Park, P. H. Chang, H. S. Park and E. Lee, “Design of Learning Input Shaping Technique for Residual Vibration Suppression in an Industrial Robot,” IEEE/ASME Transactions on Mechatronics, 11(1), 2006 pp. 55–65. doi:10.1109/TMECH.2005.863365. |
| [14] | C.-G. Kang, K. S. Woo, J. W. Kim, D. J. Lee, K. H. Park and H. C. Kim, “Suppression of Residual Vibrations with Input Shaping for a Two-Mode Mechanical System,” Proceedings of International Conference on Service and Interactive Robotics, Taipei, Taiwan, 2009 pp. 1–6. |
| [15] | S. D. Jones and A. G. Ulsoy, “An Approach to Control Input Shaping with Application to Coordinate Measuring Machines,” Journal of Dynamic Systems, Measurement,and Control, 121(2) , 1999 pp. 242–247. doi:10.1115/1.2802461. |
| [16] | S. Kapucu, G. Alici and S. Bayseç, “Residual Swing/Vibration Reduction Using a Hybrid Input Shaping Method,” Mechanism and Machine Theory, 36(3), 2001 pp 311–326. doi:10.1016/S0094-114X(00)00048-3. |
| [17] | S. S. Güreyük and S. Cinal, “Robust Three-Impulse Sequence Input Shaper Design,” Journal of Vibration and Control, 13(12) , 2007 pp.1807–1818. doi:10.1177/1077546307080012 . |
| [18] | T. Singh and W. Singhose, “Tutorial on Input Shaping/Time Delay Control of Maneuvering Flexible Structures,” Proceedings of the 2002 American Control Conference, Vol. 3, Anchorage, AK, May 8–10, 2002 pp. 1717–1731. doi:10.1109/ACC.2002.1023813 . |
| [19] | I. Arolovich and G. Agranovich, “Control Improvement of Under-Damped Systems and Structures by Input Shaping,” Proceedings of the 8th International Conference on Material Technologies and Modeling (MMT-2014), Ariel, Israel, Jul. 28–Aug. 1, 2014 pp. 3.1–3.10. (May 23, 2017) www.semanticscholar.org/paper/Control-Improvement-of-Under-damped-Systems-and-St-Arolovich-Agranovich/5cd5f119710edc81be912aea09a66c64e92d48a2. |
| [20] | C.-G. Kang, “On the Derivative Constraints of Input Shaping Control,” Journal of Mechanical Science and Technology, 25(2), 2011 pp. 549–554. doi:10.1007/s12206-010-1205-7. |
| [21] | T. Singh and S. R. Vadali, “Robust Time-Optimal Control: Frequency Domain Approach,” Journal of Guidance, Control, and Dynamics, 17(2) , 1994 pp. 346–353. doi:10.2514/3.21204. |
| [22] | D. Adair and M. Jaeger, “Simulation of Tapered Rotating Beams with Centrifugal Stiffening Using the Adomian Decomposition Method,” Applied Mathematical Modelling, 40(4) , 2016 pp. 3230–3241. doi:10.1016/j.apm.2015.09.097. |
| [23] | D. Adair and M. Alimaganbetov, “Propeller Wing Aerodynamic Interference for Small UAVs during VSTOL,” 56th Israel Annual Conference on Aerospace Sciences, Tel Aviv/Haifa, 9–10 Mar., 2016. (May 23, 2017) www.researchgate.net/publication/285356494_Propeller_Wing_Aerodynamic_Interference_ for_Small_UAVs_during_VSTOL . |
| D. Adair and M. Jaeger, “Aspects of Input Shaping Control of Flexible Mechanical Systems,” The Mathematica Journal, 2017. dx.doi.org/doi:10.3888/tmj.19-3. | |
Desmond Adairはカザフスタン共和国、アスタナ、ナザルバエフ大学工学部の機械工学教授です。 近年、振動問題を解くための解析手法の開発や計算流体力学の研究に従事しています。
Martin JaegerはクウェートのMishref、Australian College of Kuwaitの土木工学の准教授であり、工学部のProject Based Learning Centerのマネージャーです。彼の最近の研究テーマは、建設管理と総合的な品質管理、工学教育のための戦略の研究です。
Desmond Adair
Martin Jaeger