HOME > [Mathematica Journal] 最大軌道遷移問題

On the Maximal Orbit Transfer Problem
最大軌道遷移問題

 

宇宙船は円軌道であると仮定し、可変パラメータが推力方向の角度になるように、宇宙船が設定時間の間、一定の推力で遷移可能な最大可能円軌道を求める問題を考えます。 また、二つの円軌道の共通中心に 1つの引力の中心があると仮定します。 最後に、すべての定数および変数は、正規化された値であると仮定します。

このアーティクルは 5つのセクションに分かれています。 軌道遷移問題、運動方程式、最適制御問題、メイヤー問題の必要条件、そして Mathematica組み込みの Manipulate関数を用いた最大軌道遷移問題への動的なアプローチです。

地球-火星軌道遷移問題はタイムリーで、アメリカのキュリオシティ・ローバーの火星への飛行とスムーズな着陸の成功があります。

 

軌道遷移問題

軌道遷移問題について、次のように仮定します。

• 唯一の引力の中心がある。
• 最初に宇宙船は引力の中心の周りを円軌道で移動する。
• 宇宙船は時間間隔で動作するロケットエンジンからの一定の推力で移動する。
• 宇宙船は引力の中心の周りを可能最大円軌道で移動する。
• 軌道遷移軌跡は２つの円軌道と引力の中心と同一平面上にある。

これらすべての仮定は [1, p. 66] に記載されています。 次の図はいくつかの表記を伴った問題の解のスケッチです。 青い曲線は軌道遷移軌跡で、赤と緑の曲線は最初の低い円軌道と最終的な高い円軌道です。

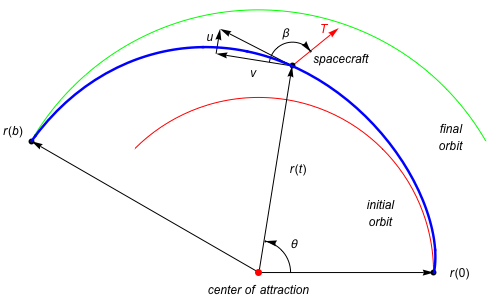
[1, pp.66-68]、[2] もしくは [3] からの表記は次の通りです。

• t は地平線と呼ばれる区間 [0,b] 内の時間である。
• r(t) は引力の中心から宇宙船までの距離であり、r(t) は燃料が燃焼すると増加する。r(0)=r₀ は初期半径で、r(b) は最後で最大の距離である。
• θ(t) は、t=0 の宇宙船の位置と引力の中心を結ぶ直線から反時計回りに測定した極角である。
• u(t) は視線方向の速度成分である。
• v(t) は接線方向の速度成分である。
• β(t) は推力方向の角度で、制御変数である。
• m₀ は推進剤を含む宇宙船の初期質量である。m₀ – m’t は時間依存の質量で、一定の燃料消費率 m’>0 によって減少する。
• T は推力で、一定であると仮定する。
• μ は重力定数である。

 

運動方程式

[1, p.67] と [2] に従う、上記の仮定に一致する宇宙船の運動方程式は、

関連する境界条件は、

非線形微分方程式の系 (1) から (4) と、境界条件 (5) から (10)、制御関数 β と最適制御問題の最大化条件

を、状態関数 r, u, v, θ と制御関数 β が十分に滑らかであると仮定して解きます。 条件 (6)、(7)、 (9)、(10) は、宇宙船の軌道が二つの円軌道に接することを保証します。 

 

最適制御問題

目標は時間の終点の軌道遷移の半径 r(b) を最大化することで、コスト関数は次の式によって決まります。

したがって地平線は [0,b] で b>0 です。 これはメイヤー最適制御問題です。([4] の Ch. 4 参照) 微分方程式 (1) から (4) と条件 (5) から (10)、コスト関数 (12) は時間に依存せず、最適制御問題は次の 2つの問題のいずれかに相当します。

• 微分方程式 (1) から (4) と条件 (5) から (10)、与えられた r(b)、有限で任意の b と b を最小にする最適条件
• 微分方程式 (1) から (4) と条件 (5) から (10)、与えられた r(b) と燃料消費 を最小にする最適条件

定理 1

Filippovの定理 ([4] の定理9.2.i) の仮説の下で、最適制御問題 (1) から (4) と条件 (5) から(10) と最大化関数 (11) と (12) は許容ペアの空でない集合中に絶対最大値を持ちます。

 

メイヤー問題の必要条件

簡潔にするために、ここでは [4] の 定理4.2.i の短縮したバージョンを示します。メイヤー問題は次のように表現されます。

ペア (x(t),u(t)), a ≤ t ≤ b は許容できる(もしくは実行できる)と言われ、 は絶対連続で [5]、は測定可能、そして x と u はほとんどいたるところで (14) を満たすことを与えます。 Ω を許容ペア (x,u) のクラスであるとします。目標は Ω 上のコスト関数 (13) の最小値を見つけること、すなわち、すべての (x,u) ∈ Ω に対して となる要素 を見つけることです。 上で乗算機と呼ばれる変数 λ=(λ₁ ,…, λ_n) と、ハミルトニアンと呼ばれる補助関数 H(t,x,u,λ) を下記によって導入します。

を定義します。

 

さらに必要な前提条件：

1. すべての (x,u) ∈ Ω に対して、 となる要素 (x*,u*) ∈ Ω が存在する。
2. A は で閉じている。
3. 集合 S={(t,x,u)|(t,x)∈A,u∈U(t)} は で閉じている。
4. 
5. 表記：
   
6. 最適軌道 x* のグラフ {(t,x*(t))|a≤t≤b} は A の内側に属する。
7. U は時間に依存せず、閉じた集合である。
8. 最適軌道 x* の終点 は B の点で、B は (いくつかの次元 δ , 0≤δ≤2n+2 の) 接線多様体 B’ を持ち、そのベクトルは
   
   もしくは
   
   で示される。

定理2

上記の 8つの仮説を仮定し、(x*,u*) をメイヤー問題 (13) と (14) の最適ペアであるとします。最適ペア (x*,u*) は必ず次の特性を持ちます：

• (a) 次の式となるような絶対連続関数 λ(t)=(λ₁(t) ,…, λ_n(t)) が存在する。
  
  もし dg が e[x*] でゼロでないなら、λ(t) は [a,b] でゼロにならない。
  
  
• (b) ほぼすべてが不変の t∈[a,b] に対して、u のみに依存する関数ハミルトニアンは最適戦略 u*=u*(t) で U の中に最小値を取る。これは M(t,x*(t),λ(t))=H(t,x*(t),u*(t),λ(t)) を示唆する。
  
  
• (c) 関数 M(t)=M(t,x*(t),λ(t)) は [a,b] で絶対連続関数と一致し、
  
  となる。
  
  
• (d) (横断関係) すべてのベクトル h=(da,dx₁,db,dx₂)∈B’ に対して
  
  となるような定数 が存在する。

(15) と定理2 の (a) から、(1) から (4) のための乗算機とハミルトニアンは

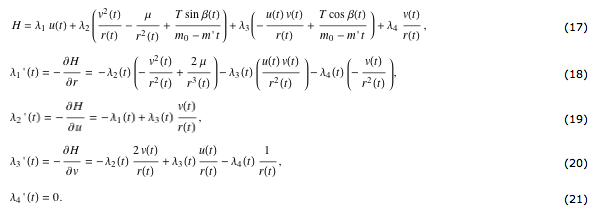
(21) と (18) から、λ₄≡0となり、 (17) から (20) は

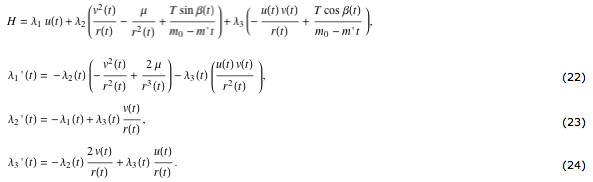
さらに、定理2 の (b) から

したがって制御関数 β は乗算機 λ₂ と λ₃ によって決まります。(4) に基づいて、極角 θ は v と r によって決まります。定理2 の横断関係 (たとえば式(16)) から、

これは変数 r, u, v, λ₁ , λ₂ , λ₃ の 6つの非線形微分方程式 (1),(2),(3),(22),(23),(24) と、6つの bilocal 条件 (5), (6), (7), (9), (10), (25) をもたらします。前述のように、変数β と θ が続きます。次のセクションでは、最大軌道遷移問題への動的なアプローチを実装しています。

 

最大軌道遷移問題への動的なアプローチ

関数 MaximalRadiusOrbitTransfer は、中心が 1つの引力の中心に位置するように、同一平面上の二つの円軌道間の最大半径軌道遷移を動的に示します。 ここで thrust はエンジンの一定の推力、dmr は推進剤流量に起因する質量減少率、b は最終時間、m0 は推進剤を含む宇宙船の初期質量、μ は重力定数、r0 は初期半径、u0 は初期視線速度、ub は最終視線速度、v0 は初期接線速度、k は推力ベクトルの数です。

問題は明らかに非線形であり、著者が知る限り、閉じた形の解は見つかっていません。 定理1によって示唆されるように、数値的方法を通して解を得る可能性が残ります。 解の精度は初期値に敏感に依存します。Methodオプションは Mathematica 9 以下に必要で、Mathematica 10 以上ではより高速な処理のためにオプションを削除します。

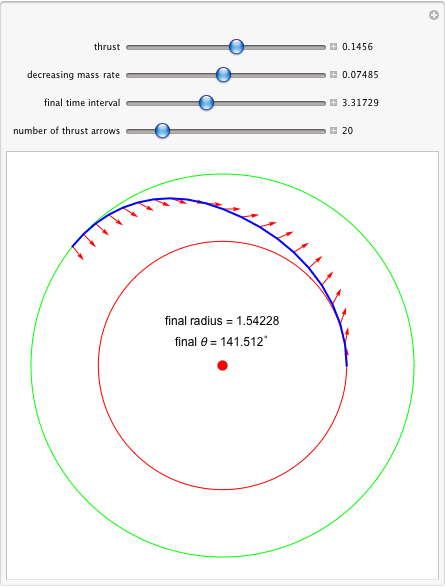
同様の画像が [6] の表紙とページ 1-2 に記載されています。

 

謝辞

ドイツのデュースブルクにあるデュースブルク＝エッセン大学数学部の名誉博士、Heiner Gonska教授の招待と温かいおもてなしに感謝を述べます。 DAAD によってサポートされる Center of Excellence for Applications of Mathematics の助成金から招待の資金が提供されました。 Aida Viziru の迅速で専門的な助力にも感謝します。

 

参考文献

[1]	A. E. Bryson and Y.-C. Ho, Applied Optimal Control: Optimization, Estimation, and Control, New York: Halsted Press, 1975.
[2]	S. Alfano and J. D. Thorne, Constant-Thrust Orbit-Raising Transfer Charts, Report PL-TR-93-1010, July 1993. www.dtic.mil/dtic/tr/fulltext/u2/a269088.pdf.
[3]	S. Alfano and J. D. Thorne, “Circle-to-Circle Constant-Thrust Orbit Raising,” The Journal of the Astronautical Sciences, 42(1), 1994 pp. 35–45. www.centerforspace.com/downloads/files/pubs/JAS.V42.N01.pdf.
[4]	L. Cesari, Optimization—Theory and Applications, Problems with Ordinary Differential Equations,Applications of Mathematics, Vol. 17, New York: Springer, 1983.
[5]	M. Mureşan, A Concrete Approach to Classical Analysis, New York: Springer, 2009.
[6]	R. Vinter, Optimal Control, Systems & Control: Foundations & Applications, Boston: Birkhäuser, 2000.
M. Mureşan, “On the Maximal Orbit Transfer Problem,” The Mathematica Journal, 2015. dx.doi.org/doi:10.3888/tmj.17-4.

 

著者について

Marian Mureşan はルーマニアのクルジュ＝ナポカにある Babeş-Bolyai University, Faculty of Mathematics and Computer Science に所属しています。彼は解析、変分法、最適制御、非平滑解析に興味があります。

 

Marian Mureşan

• Babeş-Bolyai University
• Faculty of Mathematics and Computer Science
• 1, M. Kogălniceanu str., 400084, Cluj-Napoca
• Romania
• mmarianus24@yahoo.com
• mmarian@math.ubbcluj.ro

 

 

英語原文 (HTML)

NB | CDF | PDF