| 本アーティクルは The Mathematica Journal (volume 16, 2014) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 16, 2014) and the copyright holder is Wolfram Research, Inc." |
本アーティクルでは、テンプレートに基づいたセルオートマトンのルールの表現の概念を説明します。独立したルールではなく、セルオートマトンの族を参照することで、ルールテーブルに基づいた標準的な表現を拡張します。テンプレートを得るための鍵は Mathematica に組み込まれている方程式ソルバの機能のルールです。テンプレートに適用できる操作を定義し、その使い方の例を最大の内部対称性と数の保存の性質を共有するルールの集合の表現の文脈から示します。それ以外の文脈におけるテンプレートの使用の概念も議論し、現在ある制限にも触れます。
セルオートマトンは、非常に単純なローカルルール [1] でその動作が決定されるにもかかわらず、任意で複雑な大域的なふるまいをする動的システムです。どのようにして様々な複雑なふるまいが現れるかを理解するために、セルオートマトンのルールに秘められた能力の文脈で、多くの研究がされています。例えば、密度分類問題 [2, 3] やパリティ問題 [4] などの古典的なベンチマーク問題にセルオートマトンが使われてきました。密度分類処理とは格子の初期状態が与えられとき、最も頻度の高いビットを見つけようとします。パリティ問題とは格子の初期状態が与えられたとき、1 の数のパリティを見つけようとします。これらの文脈のアプローチの1つが、対象となる問題を解く能力の意味で与えられた族のすべての可能性のあるセルオートマトンを評価することです。このアプローチは (256 のセルオートマトンからなる) 基本的な空間のような小さなセルオートマトンの族では可能ですが、2128 のルールからなる半径 3 の1次元バイナリ・セルオートマトンのような大きな族では実行できません。
大きなルールの族におけるセルオートマトンを見つけるための戦略として、内部対称性の頻度のような、候補となるルールの性質の評価に依存した進化的計算が広く使われてきました。その評価とは、これらの性質の値によって候補を破棄するか、保持するかを決めるというものです。例えば、これは WdO や現在なら密度分類問題に対して最善の半径 3 の 1 次元のルールを発見するにいたる手掛かりとなります [5]。
別の手段としては、探索空間を特定の性質を示すことが知られているセルオートマトンに制限する、というものです。ここでの問題は、どのようにして対象となる全ての部分空間を列挙する必要なく空間を制限するのか、ということです。ここで、この目的を達成する可能性のある手段としてセルオートマトンのテンプレートの概念を導入します。セルオートマトンのテンプレートは変数の使用に依存したセルオートマトンの族のメンバーのルールテーブルに関連したデータ構造です。これらの変数の導入は、個々の特定のセルオートマトンだけを表現する標準的な k 進数のルールテーブルの表現と違って、セルオートマトンのテンプレ-トがルールの集合を表現することを可能にします。Mathematica に組み込まれている方程式ソルバの能力と、ある性質を持ったセルオートマトン間で同等な関係を見つけるアルゴリズムを利用することによって、我々は数を保存するセルオートマトン (考え方として、初期状態のセルの状態数を保存している。詳細は下記参照) と最大の内部対称性を持つセルオートマトン (ルールテーブルにおいて、いくつかの変換を行っても変わらないもの。詳細は下記参照) を表現するようなテンプレートを作ることができます。ここでは、この2つをテンプレートの考えを適用させる例としていますが、他の性質にもテンプレートは適用できます。
この後のセクションでは、セルオートマトンについての基本的な概念、密度分類問題に関する重要な性質についてのセクションと続いていきます。セクション 4 では「テンプレート」の概念を説明し、テンプレートを実行するためのアルゴリズムを示します。セクション 5 ではテンプレートを使うことの利点と制限に関する議論、今後の課題へのいくつかのアイデアを述べて締めとします。
セルオートマトンは離散的な空間、時間、状態 [1] などで分散された動的システムのクラスです。比較的単純なルールによって決定されるシステムではありますが、セルオートマトンは単純な構成間の相互作用から大規模な問題を解決へとどのように導くか、という意味のあるモデルを表現できます。
セルオートマトンとは、ローカルルールに従って時間経過により状態が変化する規則的な格子状に並べられたセルによって構成されます。格子は任意の次元 (たいていは 1次元、2次元、3次元ではあるが) で表すことができ、セルの数も無限にしたり、有限にしたりできます。セルの状態はたいてい数字や色で表現され、状態がk個あるなら 0 から k -1 の範囲で変化します。セルオートマトンのローカルルールとは全てのセルの近傍の影響を表したものであり、その次の状態にどのような影響を及ぼすかを意味した隣接したセルの集合です。近傍はたいてい半径 r (あるいは範囲) によって示され、問題においては他のセルがあるセルに影響を及ぼす範囲を意味しています。状態と範囲の 2つのパラメーターを定義することによって、セルオートマトンのルール空間あるいは族が定義されます。1次元の場合で r =1、k =2 の値は (近傍は自身と両隣の 3つであり、セルは 2つの状態をとる) 、基本的なルール空間となります。これはとてもよく研究された族で、256 という少ないルールしか持たないが、極めて現像学的なものです [1] 。
今回、セルオートマトンとは、1次元の2つの状態 (k = 2) を持つ、格子内の有限個のセルで周期的境界条件 (例えば、格子が環状にその端で閉じられる) を持つセルオートマンを意味するものとします。
全てのセルオートマトンは、セルの近傍が、次のステップでどのような状態に変化するかを定めたルールによって決定されます。ルールの最も一般的な表し方はルールテーブルです。ルールテーブルは近傍のとりうる全ての状態を辞書順に、明示的にリスト化したものであり、各セルの状態に対応しています。ここでは Wolfram の辞書順序リストを用います。このリストでは左端の近傍のセルの状態が全て (k -1) の状態のときのルールが記載されており、右へとルールが記載されていきます。右端には近傍のセルの状態が全て 0 の状態のときのルールが記載されています。
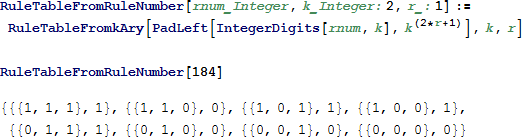
例として、ルール 184 というセルオートマトンの基本的なルールテーブルを示します。
これは k 進数の形式からなるルールテーブルの出力セルの状態の順序集合です。
k 進数の形式を示すバイナリシーケンスを 10 進数表現へと変換することによって、セルオートマトンのルール番号を得られます。この変換は与えられたルール空間におけるセルオートマトンのユニークな識別子として動作します。
ルールテーブルに関する操作を行うため、様々な Mathematica の関数が定義されています。関数 RuleTableFromkAry は k 進数の形式によるルールテーブルを入力することによって、一般的な表現方法に変換します。

関数 kAryFromRuleTable は関数 RuleTableFromkAry と逆の手順を行う関数です。

関数 RuleTabaleFromRuleNumber は、セルオートマトンのルール番号を入力することで、そのルールテーブルを決定します。
逆の関数 RuleNumberFromRuleTable はルールテーブルから、ルール番号を出力します。

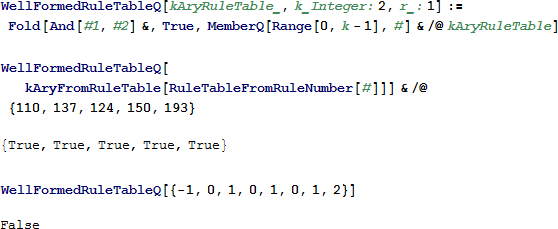
関数 WellFormedRuleTableQ は k と r の値に基づいた k 進数のルールテーブルが正しいかどうかを確認します。
関数 RuleOutputFromNeighbourfood は、ルールテーブルの特定の近傍に応じた出力を得るためのユーティリティ関数です。

最後に、関数 AllNeighbourhoods はあるルール空間の取り得る全ての近傍を与えるユーティリティ関数です。

これらのすべての関数はルールテーブルの操作を行うのに役立ちます。そして、本ア-ティクルを通してこれらを使っていきます。
1次元上では、上から下へと時間が流れるような空間-時間表を用いてシステムの展開状況を可視化できます。この時セルの状態は色によって表現します。バイナリ・セルオートマトンでは白いセルを 0 の状態、黒いセルを 1 の状態とします。与えられた格子上でルールにそって動かした結果の空間-時間表を得て描画するために、Mathematica に組み込まれている関数 CellularAutomaton と関数 ArrayPlot を使います。
セルオートマトンのルールに隠された計算の能力をより理解するために、その能力に取り組むためのベンチマーク問題が定義されています。その中で最も一般的なものに密度分類問題 (DCT) というものがあります。DCT の従来の定義は、1次元バイナリ・セルオートマトンが、初期状態に黒 (白) のセルが多いときに、任意の奇数サイズの初期状態から全てが黒 (白) で固定された状態にしなければならない、というものです。
DCT を完全に解くために、セルオートマトンがある状態のセル数の和を保存できる必要がある、ということが証明されています。それはどのような初期状態が与えられても、それぞれの状態のセルの数は変わるべきではないということです [6] 。これは DCT の従来の定義に反しています。全てが黒 (白) の状態へとなっていくためには、その時間経過中のそれぞれの状態のセルの数を変える必要があるということは明らかです。つまり、従来の定義によって定式化すると、DCT が解けないということを意味しています [2, 3] 。
現在、[5] において、十分ではないが最もよい DCT ソルバ (Wd0 として知られている) があります。それは他の重要な特性の中で適応度関数におけるルールの内部対象性を用いた洗練された進化的アルゴリズムの手法によるものです。完全な DCT ソルバは数の保存ができる必要があるという事実と合わせるように、Wd0 や他の良い DCT ソルバも同様のルール空間の数の保存のルールから、非常に小さなハミング距離持つことが知られています [7] 。
だいたいにして、DCT を解くためのセルオートマトンの能力を決定するとき、数の保存と内部対象性の 2つが重要な特性となります。そしてセルオートマトンのテンプレートの概念のよい例となります。この両方について、次に続くセクションでその詳細を説明します。しかしこれら 2つの特性は状態遷移間の確立された関係から導かれるものであるため、テンプレート内で扱いやすいということを事前に知っておいてください。
数の保存とは、空間と時間が進んでいっても初期状態からある状態におけるセルの状態の合計が変わらない、といういくつかのオートマトンで示される性質です。特にバイナリ・セルオートマトンでは、この性質は 1 の状態のセルの数はいつも同じ数であるということを意味しています。セルオートマトンのこの性質はとても便利です。例えば、車の交通に関するモデルシステムとういうものがあるとします。このモデルシステムでは、時間が経ったとしても車が出現したり、消えたりしません [7] 。ルール 184 の基本的なセルオートマトンは数の保存されるセルオートマトンの例です。
1次元セルオートマトンが数を保存できるようにするために、近傍サイズ n のローカルルール f が全ての状態遷移で次にある必要十分条件を満たさなければならないということが [8] によって示されました。
ここで、01, 02, …, 0i は長さ i の一連の 0 に対応しています。
[9] では、[8] におけるアルゴリズムを簡易にしたものが提案されました。基本的に任意の与えられたルールにおいて、近傍が 0 の状態だけで作るものと、0で始まらない近傍に関係する状態遷移を解析すれば十分である、ということが示されました。したがって、[8] で述べられているように、k n ではなく k n – k n-1 + 1 の近傍の合計となります。これは、下に示すような、数の保存をするセルオートマトンを表現するテンプレートを得るために使う条件です。
数の保存から離れて、DCT を解くためには、ルールの内部対象性もまた重要な役割を果たしています。この性質がどのように作用するかを十分に理解するために、ルール変換と動的等価なルールについての説明が必要です。この概念は任意の k 進数の場合に拡張できますが、ここでの説明ではバイナリルールに制限します。
セルオートマトンのルールテーブルを与えられたとき、動的等価なルールとなる3種類の変換を適用できます。バイナリの場合、BlackWhiteTransform はルールテーブルの全てのセルの状態を逆に入れ替えることによって得られます。2つ目の変換、LeftRightTransform は、ルールテーブルの近傍のビットを左右反転し、状態遷移の集合をもう一度順序付けすることで得られます。この2つの変換をどちらかの順で組み合わせることで3つ目の変換、LeftRightBlackWhiteTransform またはBlackWhiteLeftRightTransform となります。

ここで、ルール 110 ではどのように作用するかを示します。

最初の BlackWhiteTransform を確認してみます。

これらの変換によって、与えられた空間内のセルオートマトンが等価な動的振る舞いを持つことが簡単にわかります。例として、基本的なルール 110 のセルオートマトンが与えられたとき、この3つの変換を適用することによって、ルール {137,124,193} が得られます。これら4つのルールは同じ動的等価なクラスと言われています。これらの空間-時間図を見ることで、なぜそのように言われるかすぐにわかります。

あるセルオートマトンのルールテーブルを、変換によって得られる等価なルールの結果のセルオートマトンと比べることによって、共有する状態遷移の数を数えることができます。ある意味、これは変換に対するセルオートマトンの内部対称性の量の尺度を表しています。例えば基本ルール 110 のセルオートマトンは BlackWhite 変換に関しては 2 の内部対称性を持ちます。これは、ルール 110 とルール 137 は BlackWhite の対称性ルールを使って2つの状態遷移を共有しているためです。

一方で、ルール 150 でこの手順を繰り返すと、異なる結果が得られます。ルール 150 は BlackWhite 変換に従って 8 の内部対称性を持ちます。これは基本のセルオートマトンの尺度で取り得る最大値です。これは十分に予測できることです。なぜならルール 150 の BlackWhite 変換はルール 150 自身となるからです。事実、3つの変換のどれをルール 150 に適用してもルール 150 自身が得られます。これは 3つの変換のどれに従っても最大の内部対称性を持つということを示しています。

ルールの内部対称性の度合いは、動的等価なクラスの全てのメンバー間で性質が共有されているという状況で、適切な尺度となりえます。例えば、[5] 、[7] においては、合成された変換を使って内部対称性が最大となるルールは、DCT に関する発見の手掛かりとなりました。
セルオートマトンのテンプレートはルールテーブルの表現を拡張させたものです。表現を拡張させたことで単純なセルの状態があった場所に変数を持つことができるようになりました。結果として、セルオートマトンのテンプレートは単一のルールだけではなく、セルオートマトンのルール空間の部分集合全てを表現するほどの力を持ちます。
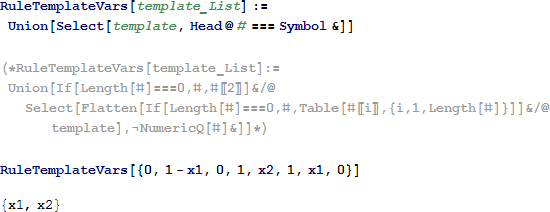
簡単な例として、テンプレート {0, 1 – x1, 0, 1, x2, 1, x1, 0} について考えてみます。これはリストの 1, 3, 5, 6, 8 ビット目が定まっていて、2, 4 ビット目は自由な変数であり、2, 7 ビット目は補完となる基本的なセルオートマトンの部分集合を表現しています。
Mathematica に組み込まれている変換のルールを使って、このテンプレートで示される4つのセルオートマトンと、対応するルール番号を得ることができます。

関数 RuleTemplateVars はテンプレート内の変数をリストします。
テンプレートから変数を取り出し、それぞれに値を適用させることで、テンプレートはそれで表現されるルールテーブルに変換されます。すべてのテンプレートは k Length[RuleTemplateVars[template]] に等しい多数の置き換えの可能性があります。しかしながら、後で説明しますが、このうちのいくつかは意味がないかもしれません。
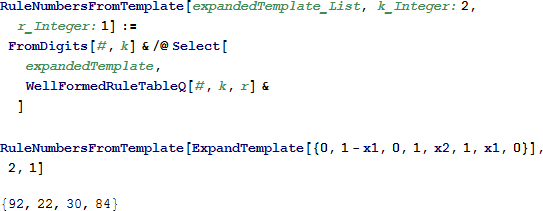
関数 ExpandTemplate は与えられたテンプレートの変数に値を適用することでこの操作を行います。この関数は 0 から k Length[RuleTemplateVars[template]] の範囲で ithSubstitution という整数をオプション引数として受け取り、変数に代入されたものとして表されます。省略した場合は、テンプレートに対して可能な全ての代入を実行します。

拡張後、関数 RuleNumberFromTemplate を使って、テンプレートで示される有効なルールのリストを取得します。
Mathematica のビルトインのシンボリック計算機能を使うと、空間全体を表現するテンプレートの作成が容易になります。基本的なセルオートマトンの空間は次のテンプレートによって表現されます。

[4] において、著者らは、パリティ問題の完全解を得られる可能性を秘めている、セルオートマトンのルールテーブルの他の遷移上で、どの遷移が、固定、可変、従属する必要があるのかを分析的に発見しました。それらの遷移を固定することで、4,294,967,296 個のルールからなる半径 2 の 1次元バイナリ・セルオートマトンのルール空間を、パリティ問題の完全解になり得る候補を 16個にまで絞り込みました。このルール空間の部分集合を表現するための基本的な構造としてド・ブラン・グラフ (de Bruijn Graph) を用いましたが、セルオートマトンのテンプレートで簡単に表現できます。
Mathmatica のビルトインの方程式ソルバの力を使って、ルールテーブルの、固定、可変、依存状態の遷移を発見するアルゴリズムを開発でき、数の保存と最大となる内部対称性の性質を共有するようなセルオートマトンを表現するテンプレートを導き出せます。次にそれらを見ていきます。
[8] において、Boccara と Fukś は保存性 (数の保存という言い方もする) を持つためにセルオートマトンのルールテーブルが満たすべき必要十分条件を確立しました。これらの条件は Mathematica で解く場合、方程式の集合を発見する BFConservationTemplate アルゴリズムへと変換することできる。この方程式の集合は決められた空間の全ての保存性セルオートマトンを表現するテンプレートと等価なものを生み出します。

基本的な空間でこの関数を実行すると、次のテンプレートが得られます。
展開すると、次のような表示が得られます。

しかし、上記の k 進数の表現が不的確なのは明らかです。なぜなら {0, k – 1} の範囲外の状態、すなわち状態が 2 と -1 であるようなものが含まれているからです。したがって、これら 3つを取り除くことによって、基本的な空間における 5つの数の保存のルールの完全な集合が得られます。

この種の戦略はセルオートマトンのルールテーブルから直接引き出される性質のみを使うということを認識することが大切です。
セルオートマトンの内部対称性もまたルールテーブルから直接引き出される性質であり、テンプレートに一般化することができる有効な候補です。セルオートマトンのルールテーブルをそれぞれの変換とともにリスト化することで、それらの間に等しい関連を確立することが可能です。Mathematica で解かせることで、3つの変換の部分集合に従った内部対称性が最大となりうる全てのセルオートマトンを表現するテンプレートが得られます。
ルールテーブルの結果全てがセルオートマトンと変換を適用したもので同じでなければならないということを確立することで、次の関数 MaxSymmTemplate はテンプレートを見つける目標を達成します。このテンプレートは引数として変換のリストに従って、内部対称性が最大となる値を示す指定された空間の全てのセルオートマトンを表現するものです。

BlackWhite 変換で最大の内部対称性を持つ基本的なセルオートマトン全てを表現するテンプレートを見つけるためには、関数 MaxSymmTemplate を実行して、ルール番号を生成するテンプレートを展開します。

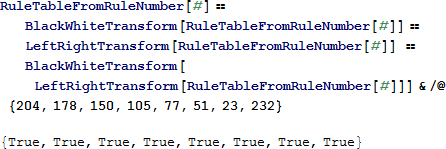
この結果の確認は、これらのルール番号全てについて変換したときに同じルールテーブルを生成することが保障されることで行うことができます。

同様にして全ての変形にしたがった最大の対称性を持つ全てのセルオートマトンを表現するテンプレートを得ることができ、その展開から対応するルール番号も求めることができます。

もう一度、それらが正しいかを確認することができます。
BFConservationTemplate 関数と MaxSymmTemplate 関数はアルゴリズムの開始点として使われるオプションの引数として別のテンプレートになることができます。これが一般的な構造を共有するテンプレートの交差を構成する現在の方法です。例えば、BlackWhite 変換に従った全ての内部対称性が最大となるすべての基本的な従来のセルオートマトンを作成するために、MaxSymmTemplate を開始点として、基本的な空間の数の保存のルールに対してこのテンプレートがそのまま使えます。これもまた、目的とするルール番号を得るために拡張可能なテンプレートとなります。

あるいは、最大の内部対称性を持つテンプレートに BFConservationTemplate アルゴリズムを開始点として使うことができ、同様の結果を得られます。

セルオートマトンのテンプレートの概念と、ルールテーブルの拡張はセルオートマトンの一般的な性質を共有できる集合のルール空間の部分集合を表現できるということを紹介しました。実際に用いた例では1次元上でのバイナリルール (基本的な空間) にしか触れませんでしたが、この考え方はより多くの状態や次元を持つ大きなセルオートマトンにも簡単に適用できるように思います。
我々は、数の保存と最大となる内部対称性に関する性質を持つセルオートマトンの基本空間の部分集合を表現するテンプレートを作る Mathematica の関数の形で、セルオートマトンのテンプレートに適用できる操作のいくつかと、いくつかの使用例を示しました。後者に関しては、テンプレートは 3つの対称性に関する変換の部分集合に対して得られます。
基本的な空間における同じ動的クラスにおけるルールのテンプレートは [10] などのセルオートマトンに関する文献にも載っています。しかし、これらの考えでは我々が提唱してきた、テンプレートに最大の内部対称性を持つルールを効果的に定義することができる、というような概念のフレームワーク全てを表現することはできません。言うまでもなく、さらに進んだセルオートマトンの性質を表すこともできません。
ここで例として使われた性質は、セルオートマトンの状態遷移間で関係が成り立っていることを示しており、それはテンプレートの形で表現される性質が必要条件であるということです。少なくとも原理上では、1次元ルールにおける可逆性の概念はテンプレートの表現に従うとは思われません。これはセルオートマトンのルールテーブルにおける可逆性がどのように特徴付けられるのか、現在知られていないためです。
内部対称性を持つテンプレートに関する現在のアルゴリズムの拡張だけでなく、他の特性のテンプレートの表現を可能にする新しいアルゴリズムの発見が今後の課題です。最大であることは必ずしも必要ではない、内部対称性の特定の値を持つテンプレートの生成も可能にする、最大となる内部対称性を生成する現在の制約を拡張することになります。
現時点では、計算資源の関係で、テンプレート展開を非常に大きなテンプレートへとうまくスケールアップをすることができません。これもまた今後、対処する必要があります。特に、テンプレートの展開の操作前にテンプレートの前処理で使われると思われる、テンプレートの和と積の操作を定義することは価値あることかもしれません。
Pedro de OliveriaはFAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo) にお礼申し上げます。Mauício Verardo はブラジル教育省の政府機関 CAPES の協力に感謝します。
P. P. B. de Oliveira and M. Verardo, “Representing Families of Cellular Automata Rules,” The Mathematica Journal, 2014. doi:10.3888/tmj.16-8.
Pedro de Oliveira は 2001年よりブラジル、サンパウロのマッケンジー長老派大学で計算情報学部と電気工学の大学院の教員をしています。彼の研究対象はセルオートマトン、進化的計算とセル・マルチエージェントシステムです。Pedro は 2003年に NKS サマースクールを卒業しました。
Maurício Verardo はマッケンジー長老派大学の電気工学分野の大学院生です。マッケンジー大学院での計算機科学の学位研究としてセルオートマトンを扱っています。Maurício は 2011年に NKS サマースクールを卒業しました。