| 本アーティクルは The Mathematica Journal (volume 16, 2014) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 16, 2014) and the copyright holder is Wolfram Research, Inc." |
本アーティクルでは、ドミノグリッドパズルを解く3つの方法を開発、比較します。「人間型」アルゴリズム、ブルートフォース法、および一般化オドメーターを使ったスキームです。
息子が学校から数字の 7 x 8 グリッドが書かれた紙を持って帰ってきたとき、すぐに興味を持ちました。目標は、パズルの各数字がドミノの数字と同じになるように、牌の山からすべてのドミノを使ってパズルを覆うことです。多くの同様のパズルはオンラインやパズルコレクションで見つけることができます。いくつかのオンラインリソースは [1, 2, 3, 4, 5] をご覧ください。これらは、ここで考える例題のソースです。
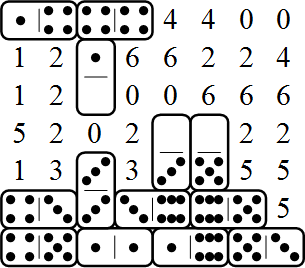
図1. ベースのパズルグリッド上に配置された 28 個のドミノのほぼ半分と、部分的に解かれたドミノグリッド。
ボード

牌の山
次に、利用可能なドミノのリストである牌の山が必要です。この場合、牌の山はダブルゼロからダブルシックスまでの全 28 種のドミノから成りますが、一般に、n(n+1)/2 個のドミノの合計に対し、任意の負でない数 n に対して定義は有効です。

位置
与えられたピース {a, b} の配置可能な位置を見つけます。
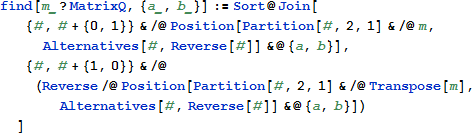
これは全ての解の力となります。始めに各列に沿ってパズルを分割し、与えられたペアに一致するものを探します。そして、転置行列上で (すなわち元の格子の列に沿って) プロセスを繰り返して、一致した位置を表示します。分割内でのペアの位置は元のグリッドの中の最初の半分のドミノの位置を与えます。しかし、適切なオフセットを加えることで、次の半分のドミノの位置も同様に与えます。そして両方とも、見つかった位置のリストの中にドミノの位置として含まれます。
ドミノの表示
次はパズル中のドミノを強調表示する関数です。関数 frameDomino は Grid の Frame オプションに含めるためのオプションを生成します。

関数 displayPuzzle はパズルグリッド (行列) とドミノのリスト (位置のペアのリスト) を受け取り、リスト中で示されたドミノの周りにフレームをつけたパズルグリッドを表示します。

例えば、m9 パズルの中にドミノ {0, 3} の2つの配置可能な位置があります
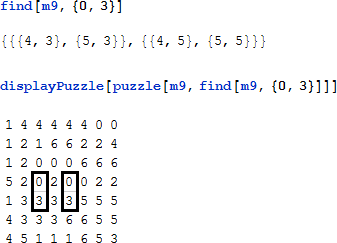
puzzle オブジェクト puzzle[m_?MatrixQ,filled_List,bones_List] は3つの引数を取ります。
m は解くパズル、つまり2次元の整数の行列です。filled は座標のペアのリストです: x1 = x2 かつ y1 = y2 ± 1 もしくは y1 = y2 かつ x1 = x2 ± 1 である場合は {{x1, y1}, {x1, y2}}bones は整数のペアのリストですFormat コマンドはパズルをどのように整えるかを定義します。パズルの行列には枠付きのドミノの配置後のリストを持ち、ツールチップは牌の山を表示します。
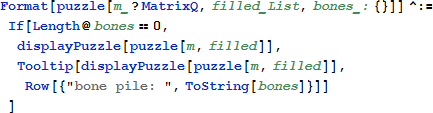
最初のパズル
このセクションはパズルの例を示します。パズルにマウスオーバーすると牌の山を見ることができます。このパズルではどのドミノもまだ使われていません。
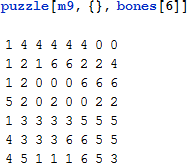
ここで、二つのピースを牌の山から取り除き、ボード上に配置します。

既に埋まったボードの位置を隠す
配置されたピースによって埋められた正方形を確認するために、空白にされた正方形を持つバージョンのボードを作成します。
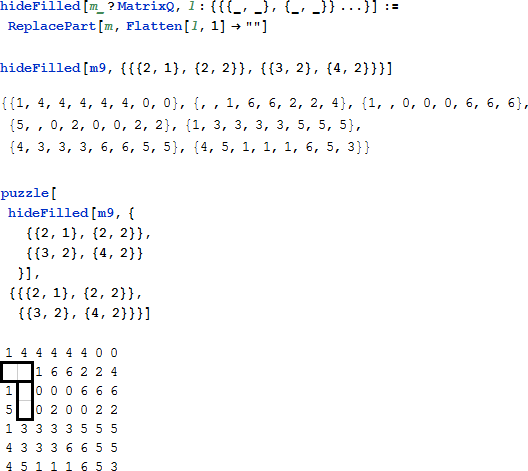
強制される位置
この関数は強制される位置を探します。一つのピースのみが強制される位置に入ることができます。
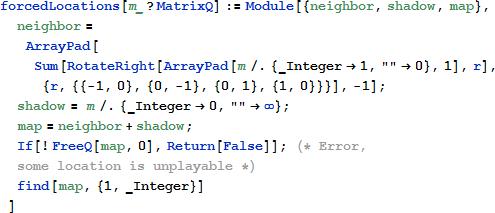
ある2つのドミノが配置された後に、強制される位置を探します。

空白で表示されているのが強制される位置です。

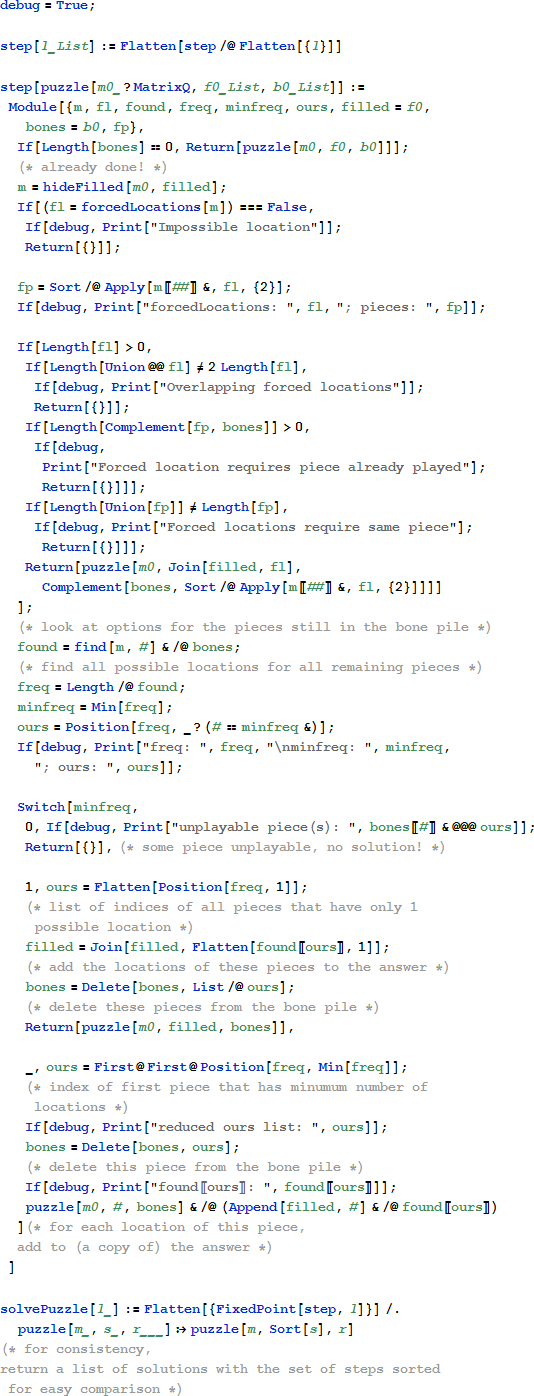
解決手法
find を使い、そして唯一の配置可能な位置を持つピースを選択する。
例
この人為的なケースにおいては、2つの強制される場所があり、それぞれの場所には、一つのピースだけを配置することができます。

関数 step は強制される場所を探し、牌の山から取った適切なドミノでその位置を埋めます。マウスオーバーで、これらのドミノが牌の山から削除されていることを確認します。

初めに、強制される位置はありませんが、強制されるピースが 4つあります。ピースはパズルの中で一つの場所にのみ配置することができます。{0, 1}、{0, 5}、{3, 4} と {4, 5} です。step 関数は一度にこれら全てを配置します。

解く!
全体のパズルを解く準備ができています。次のコマンドは現在の状態を表示し、一ステップを実行し、牌の山が空になるまで繰り返します。

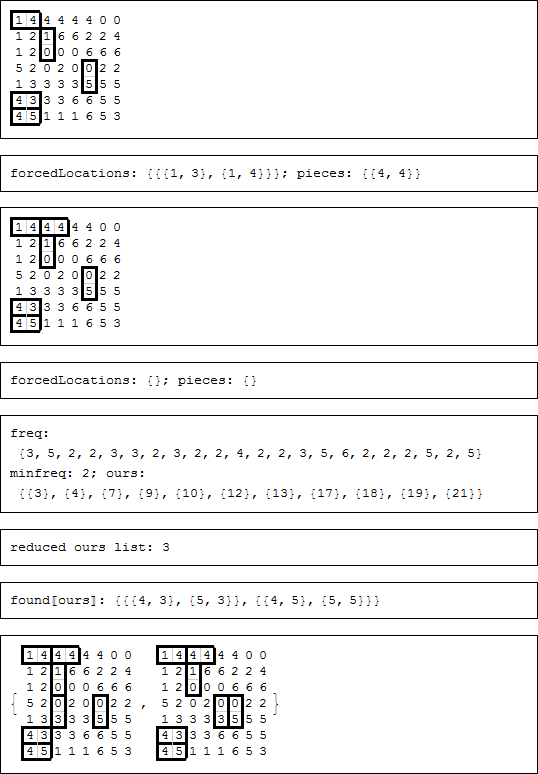
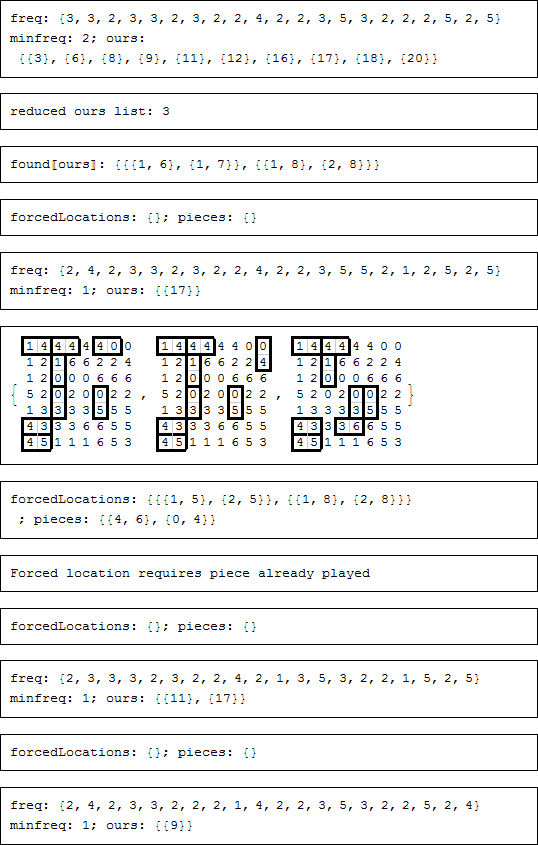
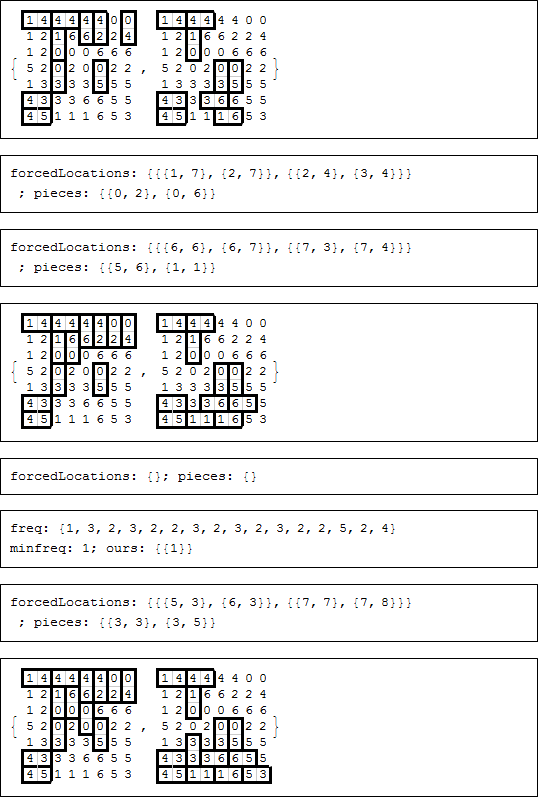


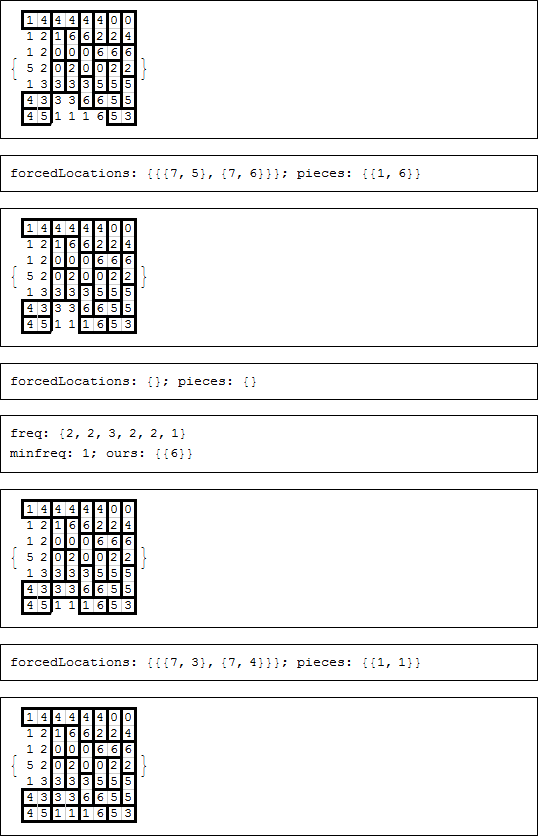
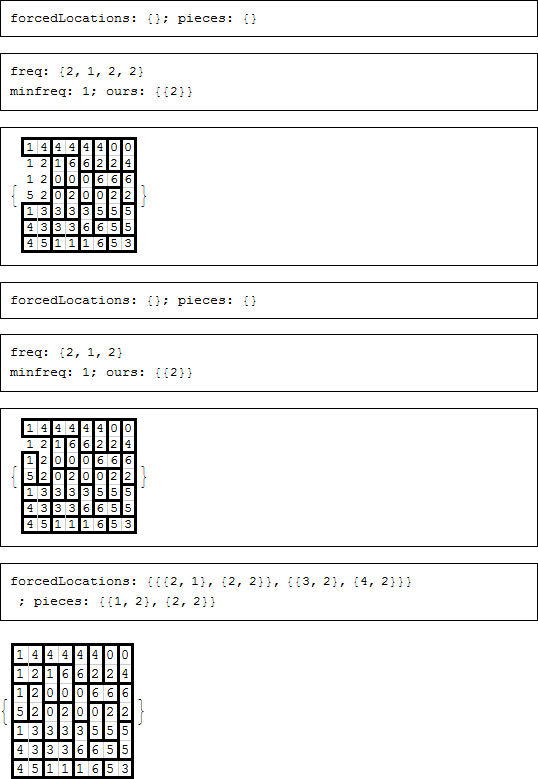
途中で、強制される場所や強制されるピースが見つからなかった場合、複数の部分的な解を考慮しなければなりませんでしたが、最終的に不一致により、一つの解が残ります。各ステップで強制される場所もしくは強制されるピースを表示するためにコメントが残っていましたが、それらをオフにします。
もう一つの表示関数
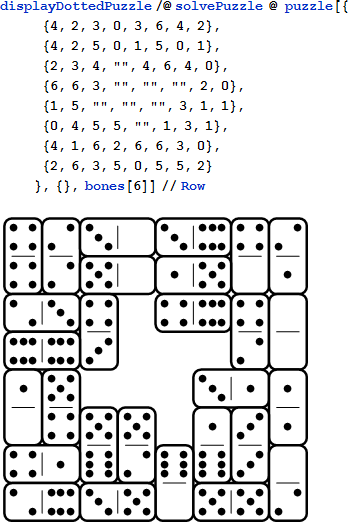
グリッドの数字のみを表示するよりも、慣例の牌の目 (やドット) でドミノを表示するより見栄えの良い表示関数を作らない理由はありません。目の位置は行列によって表すことができ、そのうちのいくつかは組み込みの行列コマンドによって簡単に作ることができます。ダブル 9 とダブル 6 のセットの目の位置は一致しているので、ここでは大きなセットを構築してみます。(ダブル-12 のセットは目の位置を調整する必要があります。)

他の行列は、手動や適切な基準を使った SparseArray もしくは Table で構築することができますが、加算と減算を使うことで簡単に作ることができます。

目は行列が 1 を持っている時は常に、半分のドミノの四角形上に配置されます。
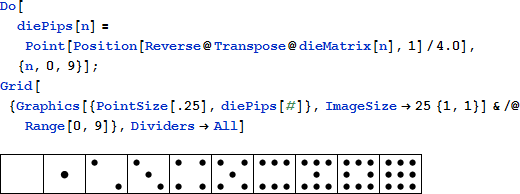
関数 displayDottedPuzzle はパズルのグラフィック表示を作成し、必要に応じて"満たさたリスト"にリストされている位置の数字をドミノ半分の図と置き換えます。そして displayPuzzle と類似の方法でドミノの輪郭を描きます。

解をアニメ化する

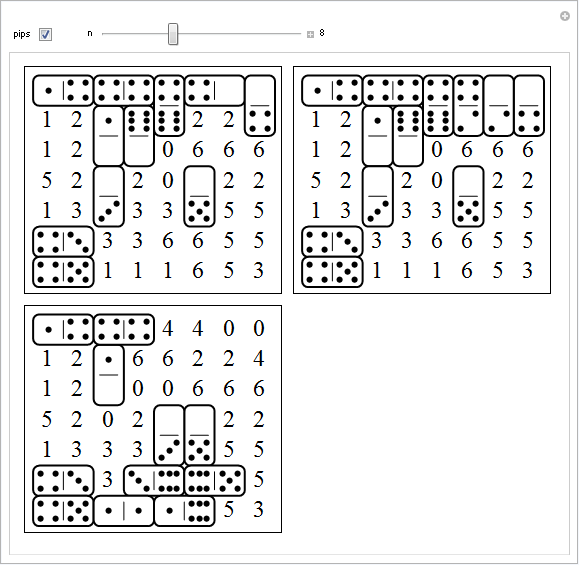
ここで述べる方法は、どのステップを実行するべきか、次にどのオプションを試すべきかを決めるために、知的に選ばれた基準を使うため、"人間型"であると考えることができます。使われる基準は次のようにまとめることができます。
人間はいくつかのオプションを削除し、より複雑な引数を作ることができます。例えば、サイト [1, 2, 3, 4, 5] の説明を参照してください (ダブルドミノを最初に配置するという一つの一般的な考えは、賢いパズルデザイナーによって簡単に破ることができます) 。順序は任意であり、修正されるかもしれませんが、次のセクションで示されるブルートフォース法よりもはるかに高速です。
下記はオリジナルのパズルの全てのドミノの配置可能な全ての位置のリストです。
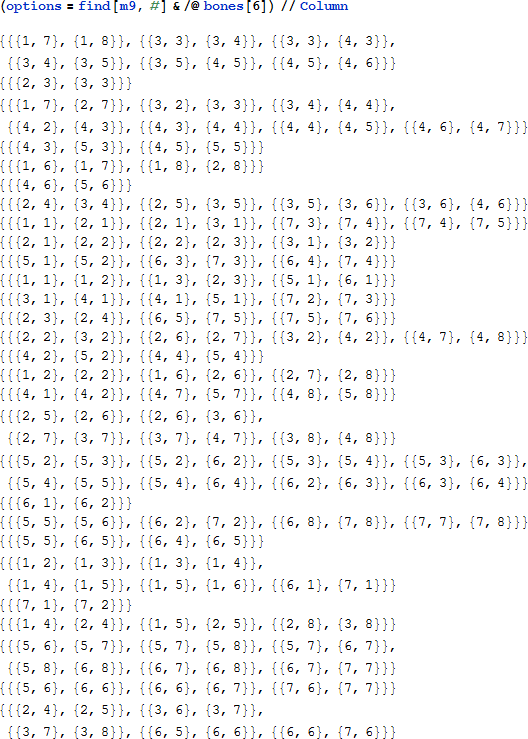
ピースの選択肢の数は大きく変動します。

(このパズルの中で、全てのダブルドミノは四個から八個の配置可能な選択肢を持っており、"最初にダブルを配置する" のは粗末な戦略であることを簡単に確認できます。) 全てのピースに対してすべての可能なオプションを取ることは、非常に大きな数を生じさせます。
考慮するにはあまりにも多くのケースです! しかし、理論上はこの方法は機能します。これらのオプションの選択のすべての組み合わせを得るために、Outer を使い、そして重なっているドミノを持たないものに Select を使います。ここでは最初の 3つのドミノのみを実行します。
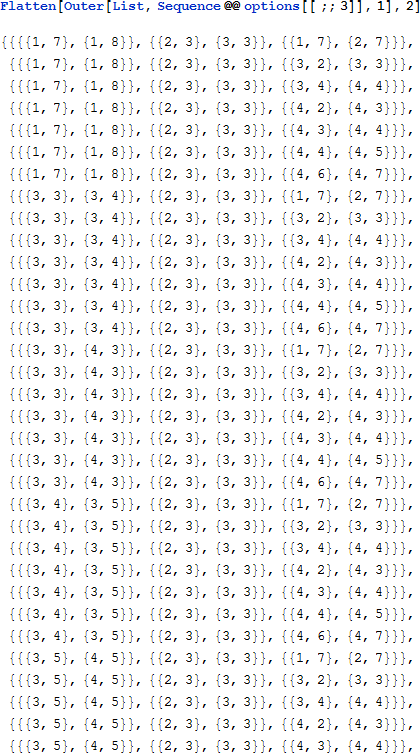
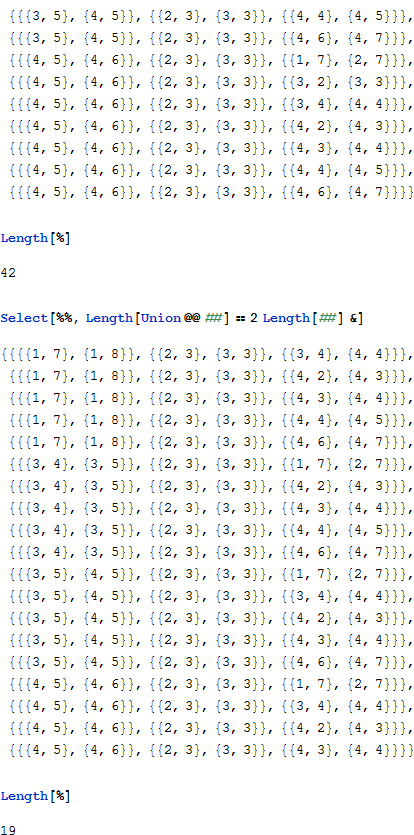
最初の 3 つのドミノを使うと、6 x 1 x 7 = 42 の可能性があり、衝突を除くと 19 に減少します。最初の 13 個のドミノを配置することは 653,184 個のケースを検討することを意味し、そのうち 4つだけが衝突がありません。
したがって次のコードは動作するはずですが、時間とメモリは法外な量になります。それは美しくシンプルで短いですが、おそらく一生の間に終了しないので、実行しないでください!

“ハンマーにはすべてが釘のように見えます。” 数年前、一般化オドメーターの考えに基づく探索-衝突検出アルゴリズムを考え出し、それ以来、どこでもそのアプリケーションを見たことあります。それはここでも機能します。
方法
28 桁の一般化オドメーターを作成します。このn番目の桁は n 番目のドミノに対して試みているオプションを表しています。全ての桁は 1 として始めます。一般にオドメーターをインクリメントすることは右端では起こりませんが、そのドミノ配置が前のドミノと衝突する最初の桁 (左側から) に起こります。桁はその最大値を超えてインクリメントされ、1 にリセットする必要がある場合に "ロールオーバー" します。桁がロールオーバーするたびに、本物のオドメーターのようにその左にある桁もまたインクリメントします。オドメーターのそれぞれの桁は、そのドミノに使用可能なオプションの数によって決まる独立した最大値を持ちます。最初の数字が最終的にロールオーバーする場合、全ての解が発見されています。ドミノオプションのリストを長さによって昇順でソートすることにより、手続きを加速させます。
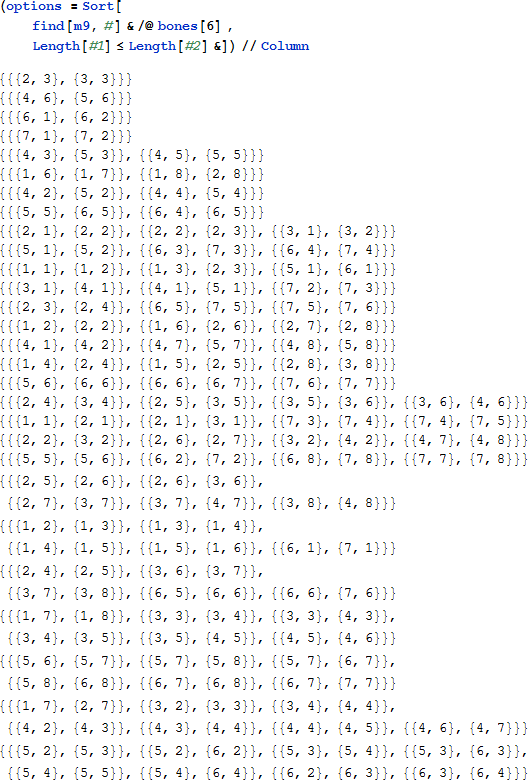

最初の 4 つのオドメーターの桁は 1 のみとなることに注意してください。それぞれ 1 から始まり、1 の最大値を持ちます。
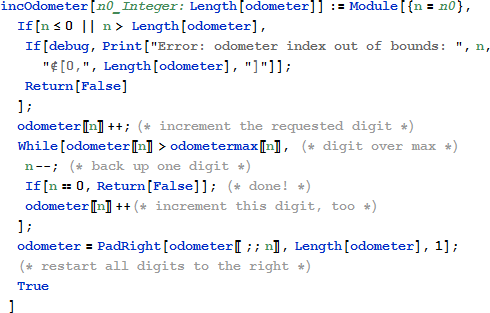
オドメーターで指定されたオプションの一部を表示もしくは使用するために、関数 MapThread を使います。
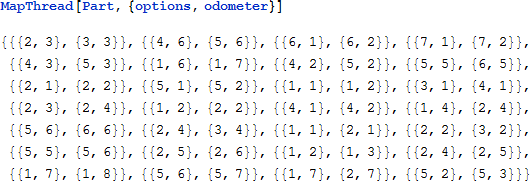
これは多かれ少なかれ、すぐに解を返すプログラムです。
予想されたように、うまくいく唯一のオドメーター表示があります。すなわち、ドミノ配置で1つの選択のみすることで、パズルを解きます。一般化オドメーター法は、予め計算することができる値をとる多数の変数を持つ状況、とりわけ、とりうる値が全ての変数に対して同じであるか、容易に特定できる方法で変化する場合に最適です。ここで選択肢はそれぞれの新しいパズルのために再計算しなければならないため、前の方法ほど効率的ではありません。
カドリール
フランスの数学者 Edouard Lucas のアイデアである “カドリール” パズル [5] は、それぞれが同じ数字を含む 2 x 2 のブロックに分割することができます。次の図は矩形配列を完全に満たしていないので、空の文字列を追加します。
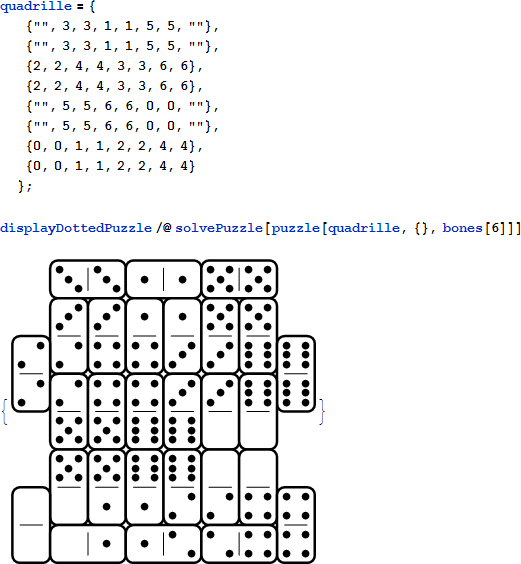
このカドリールはただ1つの解を持ちます。各ステップで強制される位置またはピースの数が多く、28 個のドミノはわずかに 4 回の反復で配置されます。
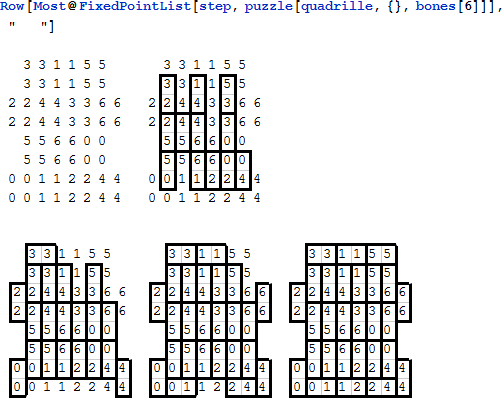
“とても簡単な” パズル
次は全てがうまくいくように感じる、とても多くの解を持つパズルです [5]!
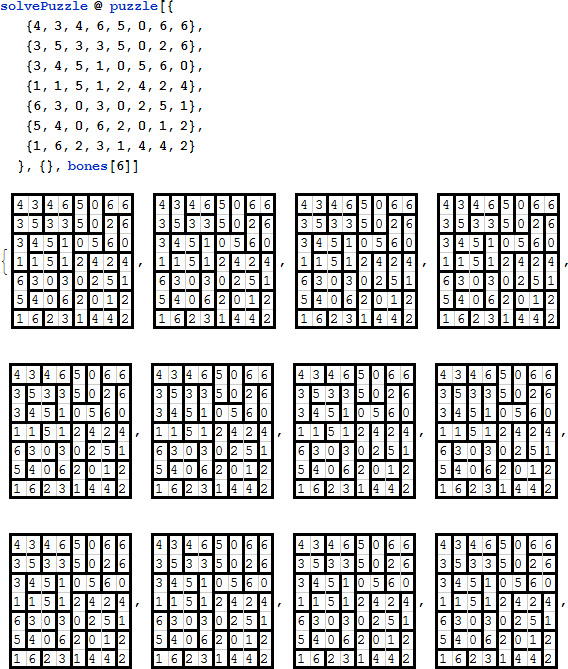


中央に穴のあるパズル
パズルが非矩形であるか、下記の [4] に示されるような意図的な隙間を持つ場合、単純に大きな四角形を埋め込み、空の文字列によって隙間を示します。
オンラインもしくはダウンロード可能なドミノ・パズル・ジェネレータは、解けることが保障されているグリッドを作成するようにドミノをレイアウトしているようです。しかし、たとえ提示されるすべてのパズルを解くことができるとしても、いくつかの疑問が頭に浮かびます。
与えられたグリッド次元に対して、いくつの異なる解がありますか? (上記の 3つの方法は個々のパズルを解きますが、与えられたグリッドの番号が全ての可能な方法により再配置されたらどうですか?)
与えられたグリッド次元に対して、1つの解のみを持つ可能なパズルの比率、また一般に、全ての に対して k 個の解を持つパズルの比率はどれくらいですか?可能な解の最大数はどれくらいですか?
ここで開発した関数という意味置いてであるということを心に留めておいてください。"解" は単にドミノの位置のリストであり、同じ次元の別のパズルは、基礎となるグリッド番号を置換または他の有効な方法でそれらを再配置することで、同じ解を持つことができます。明快さを増すことに関心がある場合、解スキーマをボードに伏せたドミノのレイアウトとして定義します。これで、与えられたパズルグリッドのとりうる明確なスキーマの数について話すことができます。
与えられたボードに対して、数字を無視して全ての解スキーマを生成するプログラムを書いてみてはどうですか?これは関数 solvePuzzle もしくは関数 odometerSolve のいずれかを変更することによって行うことができますが、どちらも書かれているジョブを完全に実行することはできません (それらを 0 入力で埋められたボード上で試してみましたが、ダブルゼロ・ドミノの牌の山を期待するように調整する必要がありました) 。
最後に、どのように人間が次にどのドミノを置くか、に従った、最初の解法が非常にうまく機能したことは興味深いです。ブルートフォース法のコードは最も単純ですが、大規模な並列処理がなければ非実用的です。オドメーター法はうまく機能しますが、ここでは "人間" の方法ほど速くはありませんし、いずれにせよ読者に分かりやすくありません。パズルを解くための方法は複数あります。もしパズルを考えることに多くの時間を費やすならば、他の方法や他の疑問が浮かぶでしょう。
私を励ましてくれたサザン・アドベンティスト大学の同僚、時折私を助けてくれた Wolfram Research の方々と私の煩わしい雰囲気に我慢してくれた Claryce に感謝します。
K. E. Caviness, "Three Ways to Solve Domino Grids," The Mathematica Journal, 2014. doi:10.3888/tmj.16-10.
Ken Caviness はサザン・アドベンティスト大学 (チャタヌーガ近くのリベラルアーツ大学) で教えています。マサチューセッツ大学ローウェル校で物理学 (相対性理論と核物理学) の博士号を取得して以来、ルワンダ、テキサスおよびテネシー州で数学と物理学を教えてきました。彼はコンピュータと (エスペラントを含む) 人間の言語に興味があり、仕事や趣味で Mathematica をバージョン 1 から使っています。