| 本アーティクルは The Mathematica Journal (volume 16, 2014) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 16, 2014) and the copyright holder is Wolfram Research, Inc." |
本アーティクルでは、「アルベロス」とよばれる古代図形における一連の特性を系統的に証明します。著者の貢献によって、新たに発見され拡張された内容も含みます。
Mathematica が提供する卓越した計算力に触発されて、私はしばらく前に「アルベロス」と呼ばれる興味深い幾何学的図形の特性の収集と実装に着手することを決めました。以来、この優れたオブジェクトに関して増加する文献が示す数多くの驚くべき発見と計算上の挑戦に感銘を受け続けています。私は類似する形状として、1960年代の連続テレビ番組「The Prisoner」に登場した天蓋付きのペニーファージング自転車の下部、(パンチとジュディの人形劇で有名な) パンチの道化帽子、一つの弧が反転する陰陽シンボルを思い出します (図1を参照) 。現在では、アルキメデスの円 (アルベロスに含まれる円) [1] に特化したカタログが用意され、アルベロス関連の特性は数学分野とコンピューター科学 [2] 領域を超えて重要な応用が行われ、オンラインで情報提供されています。
多くの著名人がこの興味深いテーマに関わっており、特に Archimedes (212 BC ローマ兵士に殺される)、Pappus (320 AD)、Christian O. Mohr (1835-1918)、Victor Thébault (1882-1960)、Leon Bankoff (1908-1997)、Martin Gardner (1914-2010) らが挙げられます。近年では、Clayton Dodge、Peter Y. Woo、Thomas Schoch、Hiroshi Okumura、Masayuki Watanabe らによって引き継がれています。
Leon Bankoff は、30年以上に渡って精力的にアルベロスに注目し、人々に刺激を与えた人物です。1979年に、Schoch が新しいアルキメデスの円をいくつか発見したことが、Bankoff がアルベロスに関心を寄せたきっかけとなっています。Schoch は、20ページの手書きのメモを Martin Gardner に送り、彼がこのメモを Bankoff に渡しました。その後、Bankoff は 10 章からなる原稿の写しを Dodge に提供しました。Bankoff の死去により、予定されていた作業は Dodge が新たな発見を報告するまで中断されました[3]。1999年、Dodge は 「自分の所有するすべての資料を分類し、3つのスーツケースにファイリングするには 5年～10年かかるだろう」と述べ、この作業は現在も進行中です。『Art of Computer Programming』の第4巻が示すように、当然のことながら重要な研究の発展には多大な時間がかかるようです。
図1. 「The Prisoner」で登場したペニーファージング自転車、パンチとジュディ、物質のアルベロス
アルベロス (ギリシャ語で「靴屋のナイフ」) という名前は、靴屋で使われていたナイフの刃の形に似ていることに由来します (図1) 。アルベロスとは、共通のベースラインを共有する3つの半円で囲まれた面領域のことです (図2) 。最初にこの数学的特性を研究したのは、アルキメデスではないかといわれ『補助定理集』 (Book of Lemmas or Aiber Assumptrum) に 4～8 の定理が収められています。しかし、アラブ語訳の Book of Lemmas で、原作がアルキメデスなのかを完全に確認しないまま、繰り返しアルキメデスについて述べられていることが明らかになり、この研究のすべてがアルキメデスによるものではない可能性があることがわかりました (この研究は偽造であると考える人さえいます[4]) 。『補助定理集』 (Book of Lemmas) は、有名な『アルキメデスの牛の問題』 (Problema Bovinum) にも収められています[5]。
本アーティクルでは、網羅的な説明を試みるのではなくアルベロスの特定の特性を列挙することを目指します。我々の目的はこれらの特性を教育学的に扱うために、統一された計算方法論を発展させることです。一連の特性を整理して、相当する述語の計算をテストして実証します。これには著者によって発見および拡張された内容もいくつか含まれています。
ここでは、最も大きい半円を「一番上の弧 (top arc)」、2つの小さい半円を「左横の弧 (left side arc)」および「右横の弧 (right side arc)」とし、左右を区別する必要がない場合には、単に「横の弧 (side arcs)」として述べます。各半径を示すには、a および b を使用します (従って上の弧は半径 a + b となります) 。「線分 (segment)」とは、1つの点からもう一方の点に向かう、始点と終点がどちらであるかを気にしない直線であり、「直線 (line)」とは、2つの点を共に通る無限の直線です。旧来では状況によって、点 A と B に交わる直線と線分の両方に AB の記号が乱用されましたが、現代の用法では、線分の長さは |AB| と示します。
以下の関数はアルベロスを表示します。
以下の関数は基本的なアルベロスを描画します。
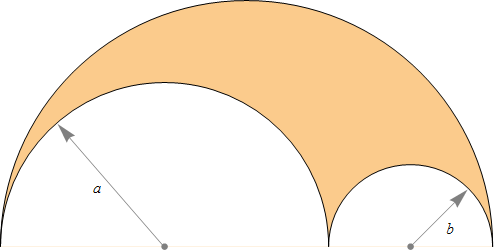
図 2. アルベロス
アルベロスの外周は、その最も大きな円の円周と等しい。
つまり、横の弧の長さの合計は一番上の弧の長さと等しくなります。この特性は興味深い逆説と関連があります [6]。
アルベロスの面積は BR を直径とする円の面積と等しい。
これは、『補助定理集』 (Book of Lemmas) の補題 4 として収録されています (図3 参照) [7, 8]。
これら２つの特性は、2つの等式を同時に試すことで簡単に証明することができます。
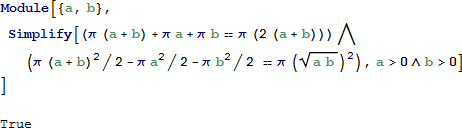
関数 drawpoints は、特定の点を赤い丸で表示するために使用します。
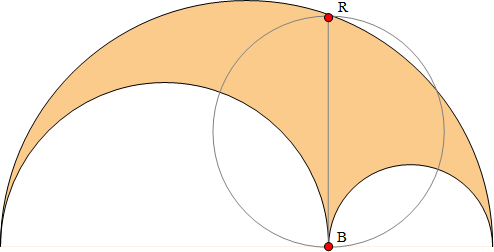
図3. を直径とする円の面積 (ラジカル円) は、アルベロスの面積と等しい。
図3 で示している円は、アルベロスの「ラジカル円」と呼ばれ、直線 は「根軸」である （この用語は一般化で詳しく述べます）。特性 3-11、25、26 を説明するために、点を描画およびラベル付けして、いくつかの座標、直線と円を図 4 に示します。
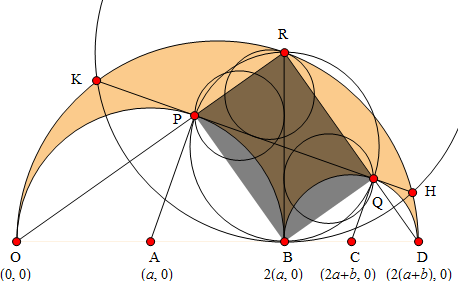
図4. 特性3 から 11、25、26 で説明する、ラベル、軸、直線と円
直線 OR と DR は直交し、横の弧の共通接線上の点 P と Q で交わる。
直線 OR と DR の直交性を証明するために、ベクトル R と D-R の内積を演算します。
点 P と Q における傾きを得るために、以下の結果を用います。
左横の弧の点 (x1, y1) の接線の方程式は
となり、右横の弧における点 (x2, y2) の接線の方程式は
となる。
関数 PQ は、接点 P と Q の座標を弧の上に配置し、定理1 に従ってそれらの接線の傾きを設定した4つの方程式の系を解くことにより、その座標を見つけます。
本アーティクルでは PQ 以外に VWS、HK、Uυ 、EF、IJr、LM を点と量の定義に使用します。
関数 dSq は任意の2つの点の距離の 2乗を計算します。
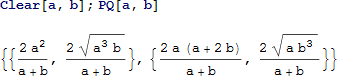
点 P と Q は、ラジカル円上にある。
BR は、ラジカル円の直径であるため、P と Q からラジカル円の中心（つまり点 (B + R)/2 ）までの距離が等しいことを証明するだけで十分です。
直線 PQ を点 H と K で、一番上の弧と交差させる。すると、H と K は中心 R と直径 BR からなる円上に存在することになる。
一番上の弧、および直線 PQ 上に点 H と K を配置する連立方程式を解くことでこの２点の座標を求めます。
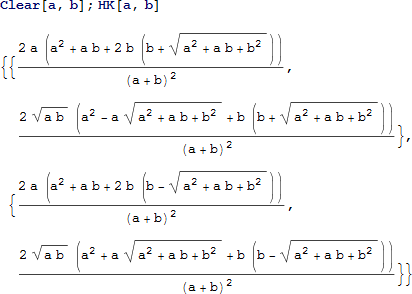
H および K から R までの距離が、B から R までの距離と同じであることを確認することによって、特性5 を証明します。
直線 AP は、直線 CQ と平行である。
これは、ベクトル P – A と Q – C の行列式（外積）はゼロであるということと同等です。
直線 AP は、直線 HK に対して垂直である。
これは、ベクトル P – A と H – K の内積はゼロであるということに相当します。
中心 C と 半径 r からなる円の表記に 
(C, r) を使用することにします。
O, P と D, Q のペアは、円 (R, BR) における逆のペアである。
円 (γ, ρ), γ ≠ p における、点 p の逆は |γ – p| |γ – u| = ρ2 [9] のような特異点 u であると定義されます。関数 inversion はこの概念を実装します。
次に D の座標を (2(a + b), 0) に戻して、特性8を証明します。
(R, BR) を反転の円であるとする。点 B、H、K はそれ自身に反転する。線分 PK は、弧 OK に反転し、線分 QH は、弧 DH に反転する。弧 OB と BD はそれ自身に反転する。ラジカル円は直線 OD に反転する。
直線 AP および CQ は、ラジカル円の接線である。
これは、対応する弧がラジカル円に直交するという主張と同じです。特性8に従って、反転のペア [10, 11] を通るように、弧は直径 BR からなる円に対して垂直となります。
BQRP は長方形である。
これは、Bankoff の驚くべき発見の一つです [12, 13, 14]。すべての4つの点がラジカル円上に存在するため、PQ が RB を二等分することを証明すれば十分です。
以下の Manipulate は、特性 3-11 を示します。最も簡単に、点 P, Q, H, K を定義する方法は、式をコピー&ペーストすることです。
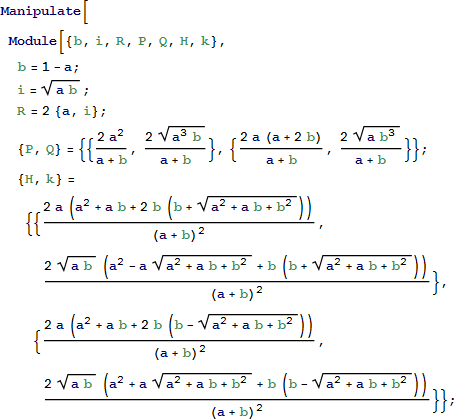
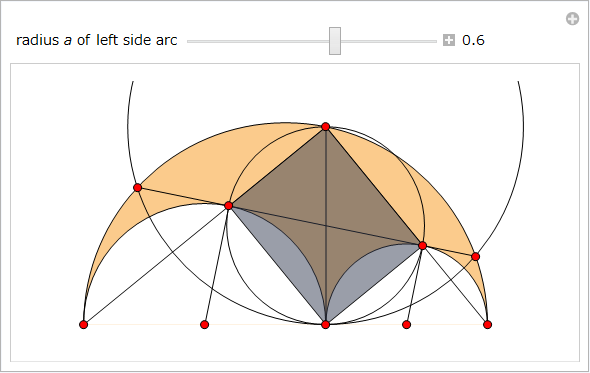
次は、横の弧と一番上の弧に接する円（点 V, W および S からなる 内接円 (U, υ) ）について検討します（図5 [15, 16] 参照）。また、横の弧の上部の点、X と Y についても検討します。
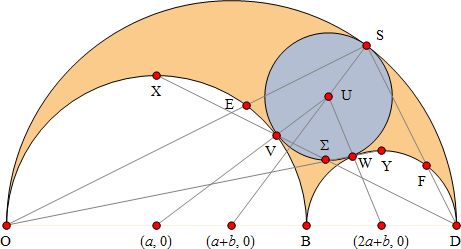
図 5. 特性 12 から 15 で説明する、内接円 (U, υ) および軸、線と点
『補助定理集』(Book of Lemmas) の定理6 で、υ の値 (内接円の半径) について述べられています。関数 Uυ は中心 U および、半径 υ の座標を計算します。
接点 V, W, S の座標は、アルベロスの３つの弧の中心と内接円を結んでいる直線の交点として取得されます。
点 X, V, D は同一線上となる。 点 O, W, Y は同一線上となる。直線 DX と OY は、内接円上の点 Σ で交差する。
共線性を確認する行列式の基準を用いて、最初の 2つの主張を証明します。
直線 DX および OY の交点を Σ (x, y)とする。ここから U までの距離が、υ からと同じことを確認すれば３番目の主張を証明することができます。
点 O, B, W, S は中心 X からなる円上に存在する。同様に、点 D, B, V, S は、中心 Y からなる円上に存在する。
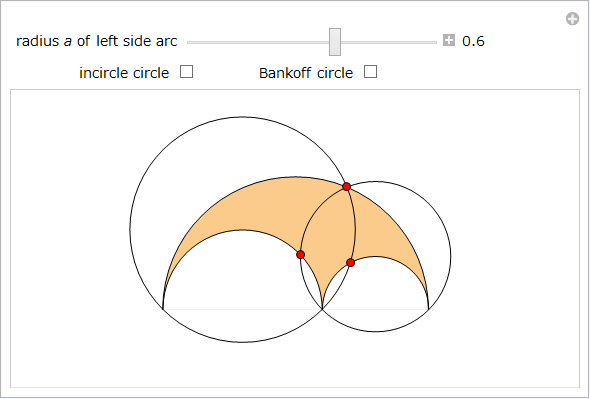
以下の Manipulateは、特性 13 [17] を示します。弧と内接円を結ぶ三角形の内接円として Bankoff の円を示すオプションは特性 23 に相当します。
Δ を OD に平行な内接円の直径とし、Δ を Δ の OD への射影とする。線分 Δ および Δ の間の矩形は正方形である。
この特性は、以下の Manipulate を使用して示し、簡単に証明することができます。
直線 OS と DS が横の弧で交差する点を、E および F とする。すると EBFS は、特性14で述べた大きさとほぼ同じ大きさの正方形となる。
まず、点 E および F を各線とそれらの弧の交点として取得し、結果を変数 replaceEF に保存します。
B の周りに F – B を 90° 回転して得られるベクトルと等しくなるように E を設定し、F -B で E を移動して得られるベクトルと等しくなるように S を設定して、特性15 を証明します。
b = 1 – a および 0 < a < 1 と仮定すると、以下のプロットは２つの正方形の大きさを比較します。
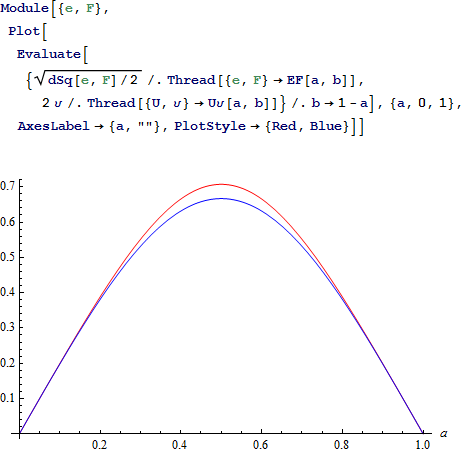
以下の Manipulate は、特性 14 と 15 を示します。
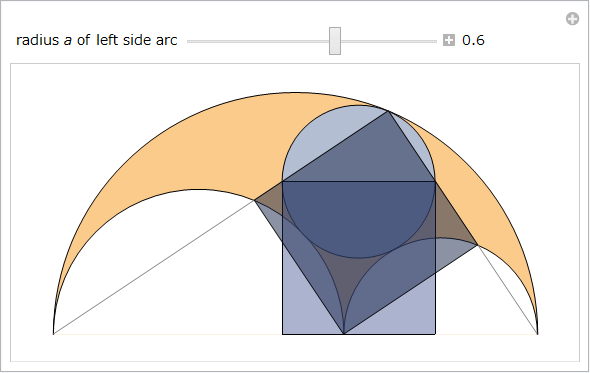
図6 において、根軸、横の弧、一番上の弧に接する2つの灰色の円を検討します。これらは「双子の円」または「アルキメデスの円」と呼ばれます。以下で示すような驚くべき特性があるために盛んに研究が行われています。特性のリスト [3, 18, 19] 内で、際立つ現象をまとめます。
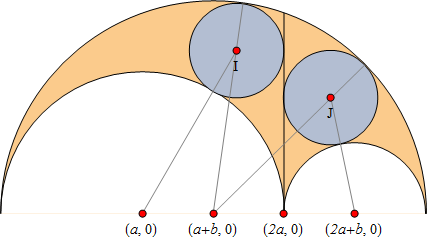
図6. 双子の円
根軸、一番上の弧、およびアルベロスの横の弧の一つに接する2つの円は同じ半径を持つ。
この特性は『補助定理集』(Book of Lemmas) において定理５として示されています。以下の６つの式の系を解いて半径の値を求め、それらが等しいことを証明したら、中心 I, J を計算します。
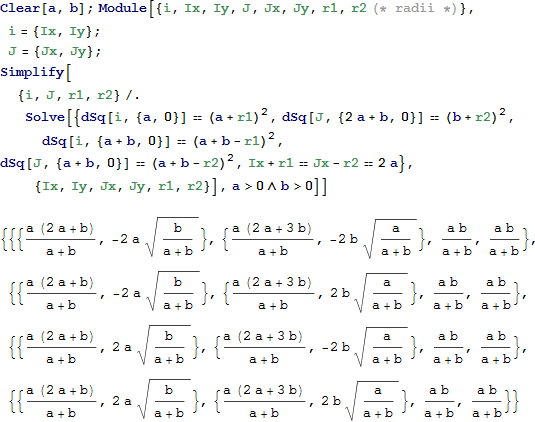
これら4つの解から (I*, J*), (I*, J), (I, J*), (I, J) のペアの中心が得られます。ここで、I* と J* は、アルベロスの直径における、I と J の鏡映であり、最後の式のみが有効です。 結果として、双子の円が確かに同じ半径 r = a b / (a + b)であることも示されます。双子の円の半径と等しい半径を持つ円は、すべてアルキメデスの円と呼ばれます。抵抗として、a と b を検討すると、r がよく解釈できるようになります。その結果、r は a と b を平行に接続することで生じる抵抗であり、つまり 1/r = 1/a + 1/b となります。関数 IJr は、中心の値と、双子の円の半径の共通の値を計算します。
アルベロスの面積は、双子の円を囲む最も小さい円の面積と等しい。
両方の双子の円に接し、中心が点 U = (x, y) で半径が v の円を検討します。 すると、v の可能値は２つ存在します。
v の極値を見つけるために、上記の各式の導関数を 0 に指定して x の値を求めます。
すると、双子に接する最小および最大の円の中心は根軸上に位置します。さらに、この結果で確認できるように、それらは同心円です。
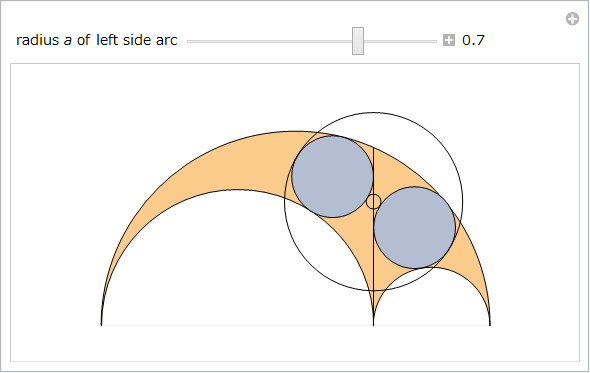
従って、特性 2 を用いて最大の正接円 (双子を囲んで最小である) が、特性17 を満たすことを確認します。以下の Manipulate は左横の弧の半径 a を変化させるにつれて、双子に接する円を示します。
以下のプロットは、根軸上に中心を持つ双子に接する 2つの円の半径を比較します。
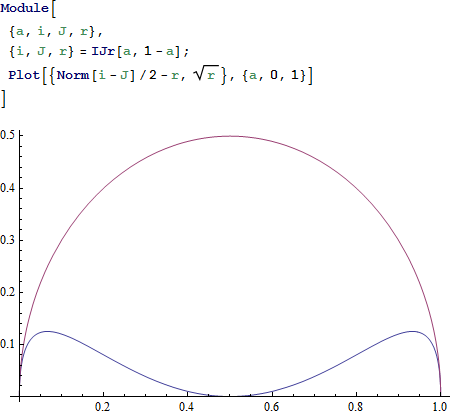
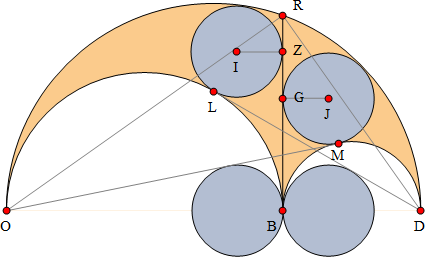
図 7. 特性 18 から 24 で説明するラベルと線
L において左側の弧と双子の円が接する共通接線は D を通る。同様に、M において右側の弧と双子の円が接する共通接線は O を通る (図7参照)。
以下は、接点 L と M を計算します。
定理1 を使用して、両方の主張を証明します。
DL の長さは、DR の長さと等しい。OM の長さは、OR の長さと等しい。
両方の主張を同時に証明します。
しかし、点 L, I, R は D を中心とする円の上にはなく、また、点 R, J, M も を中心とする円の上にはありません。そうでなければ、以下の式はゼロになります。
直線 DL は、線分 BZ を二等分する。直線 OM は、線分 BG を二等分する。
線分 BZ の長さは I の縦座標であり、線分 BG の長さは J の縦座標であるため、傾きを確認して、これらの線分の中点が前述の線上に位置することを証明すれば十分です。
B を通る OD 上に直径があり、直線 OM と DL に接する２つの青い円はアルキメデスの円である。
これは Bankoff [20] によって発見された、4番目と 5番目のアルキメデスの円です。この特性を証明するために、以下の結果 [21] を使用します。
異なる点 A (x1, y1) と B (x2, y2) へ通り抜ける直線と点 P (x, y) の距離は、
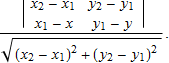
である。
この有向距離は、三角形 PAB が反時計（左）回りで横切った場合は正となり、そうでない場合は負となります。関数 dAB はこれを実装します。
点 B の左側の青い円の中心を (x, 0)、および半径を r1 とします(図7)。以下の系を解くと、 r1 の値が分かります。
同様に B の右側の青い円の半径も計算されます。これは r1 と等しくなります。
従って、主張どおり両方がアルキメデスの円です。以下の Manipulate は双子の円および、これらの２つの別の円を示します。
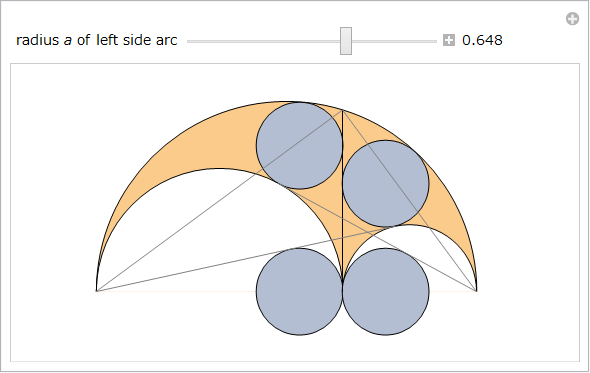
V, W, B を通る円 (図5) は Bankoff の円と呼ばれ、アルキメデスの円である。
元の双子の円はアルキメデスが発見し、1950年 [22] に Bankoff がこの 3つ目の円を発見してさらに発展させました。Bankoff の円の中心 T の座標は、T から点 V, W, B までの距離を等しくすることで求めることができます。
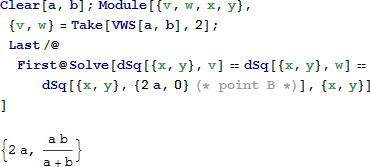
Bankoff の円は、横の弧の中心とアルベロスの内接円の中心 U に結合することで形成される三角形の内接円である。
定理2を用いて、三角形の横までの U の距離を計算し、この特性を証明します(dAB は有向距離を計算するため、行を記述する引数の順番は重要です)。
円 (O, 2a)、 (D, 2b) および一番上の弧に接する A4 = (α, γ) はアルキメデスの円である。
以下は、α と γ の値を計算します。
円 A4 は の縦軸が正の場所にあります。α は根軸上にあるのではないことに注意してください。
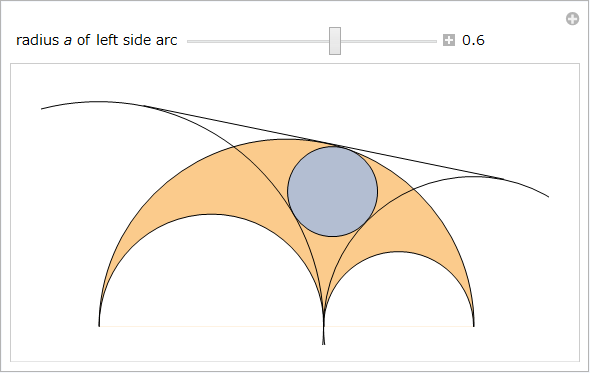
根軸に接する円 A5 と A6 は、一方が点 P を通りかつ、他方が Q を通る場合、これらは共にアルキメデスの円である（図4参照）。
直線 HK に接し、かつ R で一番上の弧に接する円 A7 は、アルキメデスの円である（図4参照）。
中心が S (x, y) で、半径 r が直線 HK に接する円は、直線 HK に接する半径 r が、S から HK までの距離が r であるので、この方程式は以下のままです。
円は R を通るため、
となります。
円は A7 は一番上の弧に接するため、
となります。
この入力では、これら3つの式を成立させる x, y, r に陽的表現を使用します。
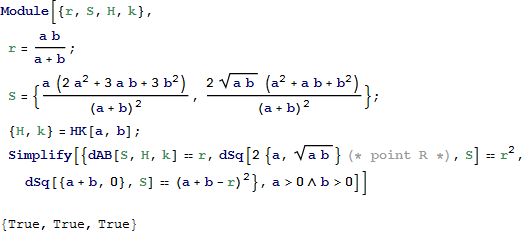
一番上の孤の中心とアルベロスの左右の弧の上部中央の点 X と Y に接続する2つの (赤い) 線分を検討する。これらの線分の長さは同じであり直交する。X と Y でこれらの直線と接し、かつ一番上の弧とも接する円、A8 と A9 はアルキメデスの円である (図8 参照)。
この特性は、1998年の夏 [23] に発見されました。
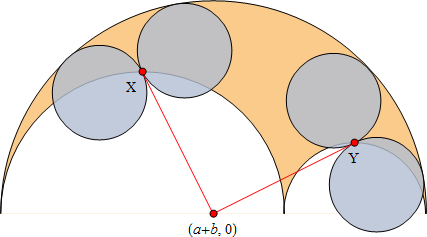
図 8. 特性27を示す、2対のアルキメデスの円
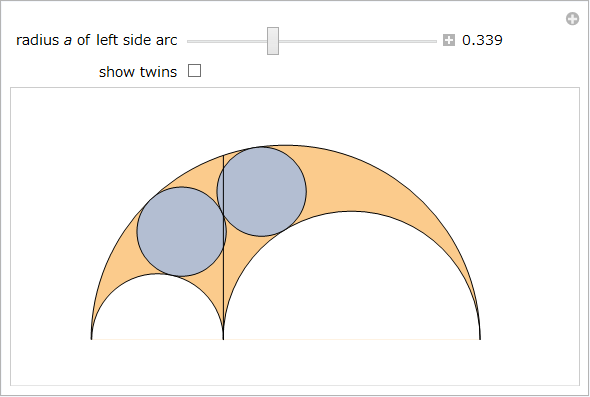
双子の円以外にもアルキメデスの円があることをみてきました (Bankoff の円および特性 21 から 27)。つまり、アルキメデスではない双子の円も存在します (これは半径が同じペアの円ですが、双子とは異なっておりアルベロス内で特定の場所に出現します)。
傾いた双子の円 は、どちらかの横の弧と一番上の弧に接していることに加えて、双子となる予定の 2つの円自身が接線となることができ、根軸に接している必要はないと初めに仮定することによって発見されました。これらの円の半径が等しくなくてもよいとすれば、解は無数に存在します。半径が等しいと仮定して開始したら、これらの円が根軸に接することを発見して終わってしまうかもしれません。しかし、そうではないことが判明しました。中心が h (x1, y1) と k (x2, y2) にあり、共通の半径 r を持つ円を検討してみましょう。5つの方程式の系を解くことで、r の値を得ることができます。
これらの式は、異なる符号の平方根を含みます。正符号を使用した式は、a = b で発散して却下されます。
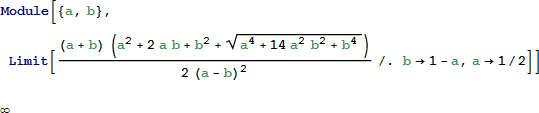
もう一方の式は、収束します。
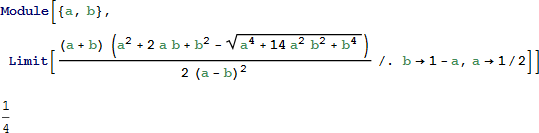
結論として、傾いた双子の円は確かに合同であり、それらに共通する半径 r は、
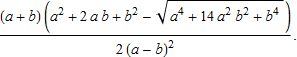
となります。
以下の双子の円と傾いた双子の円の半径の比較は、それらの違いは非常に小さいことを示しています。
これは、傾いた双子の円の中心の座標を提供します。
以下の Manipulate は、傾いた双子の円を示し、任意で a を変化させるにつれて双子の円も示されます。
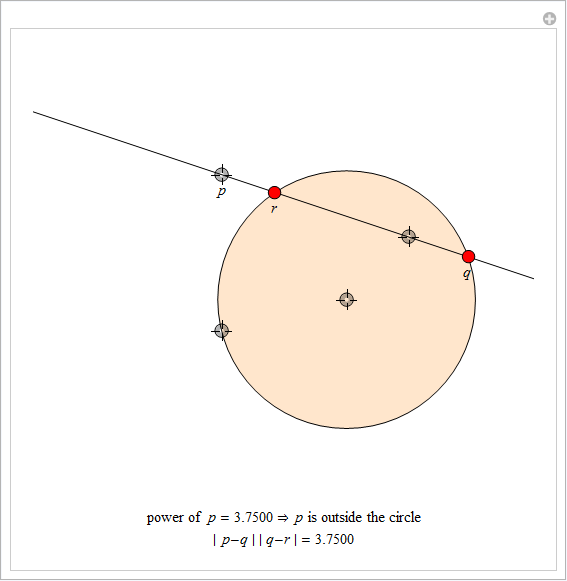
本セクションでは、弧の交差を認め、3次元のバージョンを検討することによって、アルベロスの形状を一般化します。こうした一般化の背景を設定するには、まず、2つの円の根軸 の概念が必要です。
p を点に、σ を円 (h, r) とします。σ に対する p の累乗は、実数 |h – p|2 –r2 として定義されます。p の累乗は、正数、ゼロ、負数になり、p が σ [12] の外側、上、内側のどこにあるかに依存します。f (x, y) = a (x2+y2)+ bx + cy + d として、σ の点が f (x, y) = 0 を満たす場合、p = (u, v) の累乗を定義する別の方法は、f (u, v) の値を求めることです (a = 0 ならば、類似した結果が示されます。円が線に退化する場合、f (u, v) の符号は p が線の上部にあるか、線上にあるか、線の下部にあるのかを示します)。
点の累乗には非常に興味深い特性があります。 円および点 p を前提として、p を通過して、点 q および r で円に交わる任意の直線を選択します。その際、|p – q||q – r| の積は p にのみ依存します ( を通る線の選択とは関係ありません)。この積は p の累乗と等しくなります。
以下の Manipulate で、4つのロケータをドラッグして、円の大きさ、p の位置および p を通過する直線の傾きを変更します。
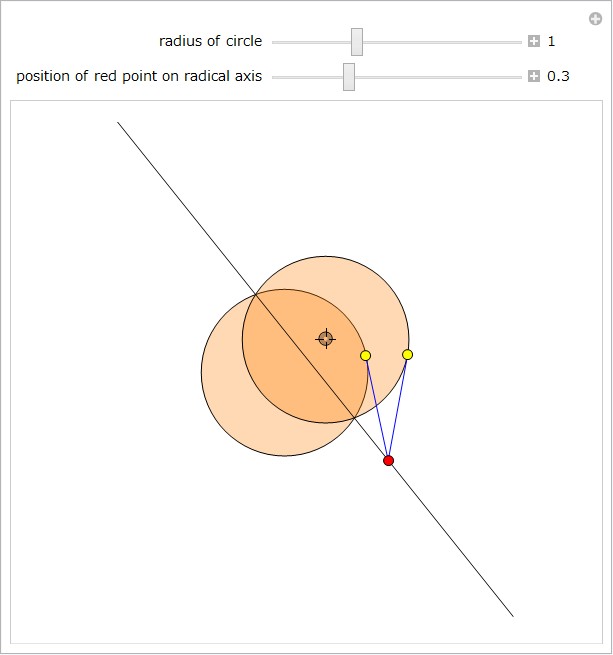
中心が異なる 2つの円を前提とすると、「根軸」とは、すべての点が各 2つの円に対して同じ累乗から成る直線であると定義されます。以下の証明は [10] で確認することができます。
2つの円が B1 と B2 で交わると、それらの根軸は共通の割線 B1B2 となる。2つの円が B で接すると、それらの根軸は B における共通の接線となる。
中心が同一線上にない 3つの円を考えると、ペアに取り込まれる 3つの根軸は、現在の直線とははっきり区別される。
2つの円の根軸は、両方の円に描かれた長さが同じ接線からの点の軌跡である。
以下の Manipulate は 2つの円を示します。一つは固定で、もう一方はロケータをドラッグするかスライダーで半径を変更することで中心と大きさを変更することができます。定理4 を説明するために、他のスライダーを使用して根軸上の赤い点を移動することができます。
以下の Manipulate は、2つの一般化を示します。
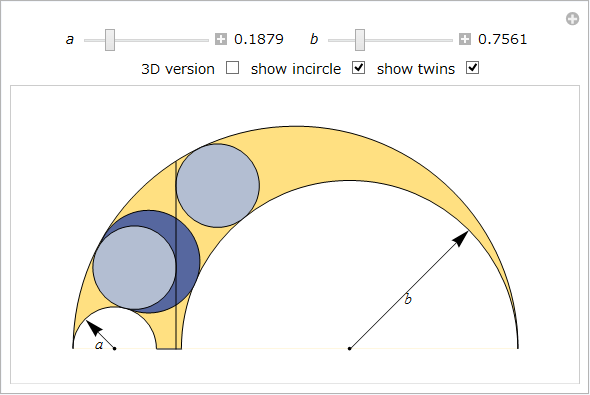
横の弧の根軸と一番上の孤と一般化されたアルべロスの孤のどちらかに接する内接円は同じ半径を持つ。
底辺間の間隔の長さを g として(一番上の弧の直径が 2a + g + 2b となるように)、x 軸からなる根軸の交差の横座標を v とすると、想定される原点は、アルベロスの最も左の点 [10] になります。
円 σ1 = (c1, r1) と σ2 = (c2, r2) が交差しない場合、|p – c1|2 – |p – c2|2 = r12 –r22 というように、それらの根軸は点 p において線分 c1c2 と交わる。
この定理を活用して、v の値を計算します。
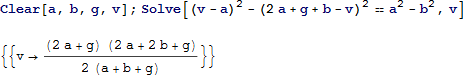
一般性を失うことなく 0 < a < 1, 0 < b <1 および -2 < g <2 （g は負数になり得ます）と仮定することができます。内接円を (α, ρ) および (β, σ) とします。これらのパラメータの値は次のように得られます。
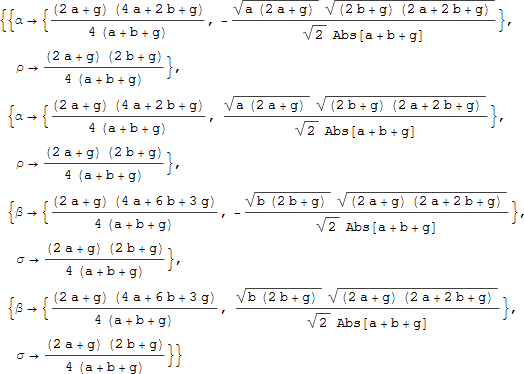
その結果、いくつかの中心が無視されることがあっても、あらゆる場合において半径は同じです。
最後にアルベロスの特性をさらに 3つ示します。 [24, 25] の操作を試して、どのような特性が含まれていると想定できるか考えてみましょう。
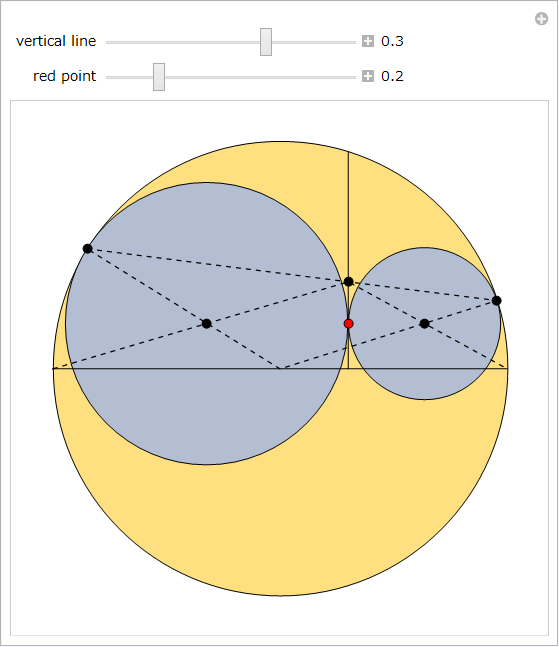
以下の最初の Manipulate を使用すると、横の弧を体系的に移動することができます。
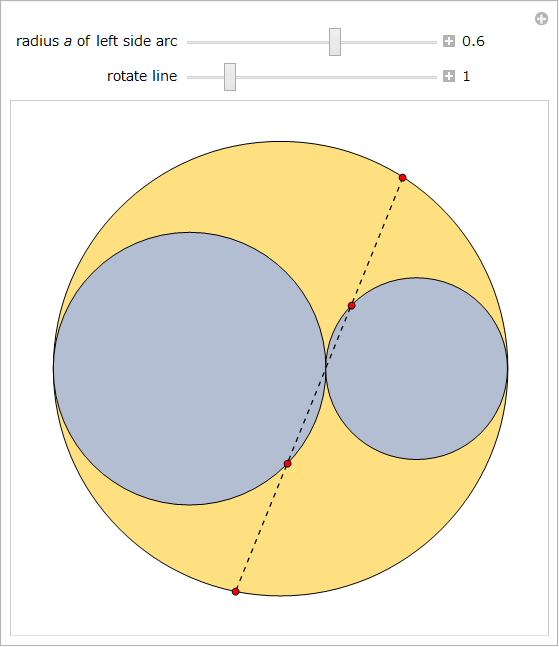
次の 2番目の Manipulate によって、直線を横の弧の接点の周りに回転させることができます。
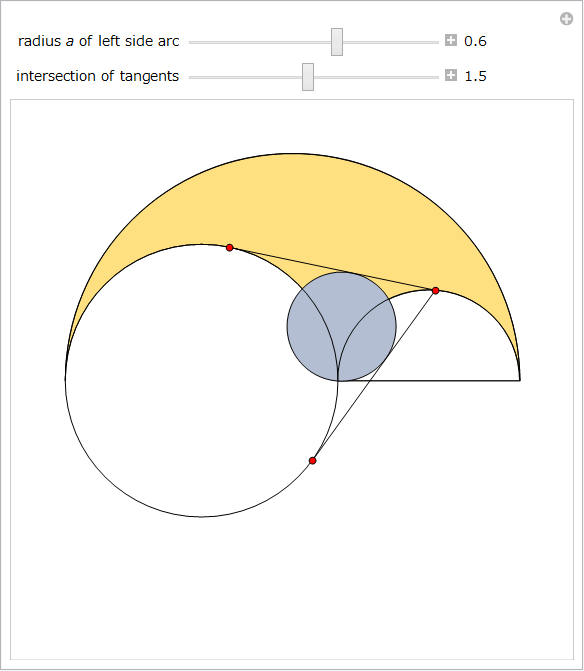
最後に 3番目の Manipulate で、無限大の双子群が示されます。
J. Rangel-Mondragón, “The Arbelos,” The Mathematica Journal, 2014. dx.doi.org/doi:10.3888/tmj.16-5.
Jaime Rangel-Mondragón は、英国・ウェールズ大学バンガー校 (UCNW) において、応用数学および計算数学の修士号と博士号を取得しました。Wolfram Research, Inc の客員研究員であり、現在は UCNW、メキシコ大学院大学・Center for Research and Advanced Studies、モンテレイ工科大学、ケレタロ工科大学、ケレタロ大学メキシコ校の情報学部に籍を置いています。現在は、組み合わせ論、計算理論、計算幾何学、都市交通、レクリエーション数学の研究も行っています。