| 本アーティクルは The Mathematica Journal (volume 16, 2014) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 16, 2014) and the copyright holder is Wolfram Research, Inc." |
本アーティクルでは、システムの信頼性ブロック図を示すために、有向非巡回グラフを使用して、複雑なシステムの信頼性を示す厳密解析式を生成する方法を説明します。さらに信頼性ブロック図に格納された統計情報を使用して解析式をシステムの信頼性のための経時的関数に変換する方法についても示します。
信頼性という用語には数多くの解釈が存在しますが、一般的には、デバイスやシステムが必要な時にタスクを問題なく実行できる能力を指します。正式には、定められた時間および特定の動作環境 [1] において、適切に機能する確率であるとされています。数学的には、信頼性関数は以下で定義されます。
ここで、T はデバイスまたはシステム寿命を示す非負の変数です。
少なくとも2つのコンポーネントから構成されるシステムの場合、各コンポーネントおよび、それらの関係によって、システムの信頼性が決まります。これらの関係は、信頼性ブロック図 (RBD) を使用して表すことができます。
通常、単純なシステムの場合、RBD コンポーネントは直列または並列配置で示されます。直列システムの場合は、すべてのコンポーネントが十分に機能する必要があります。並列システムの場合は、少なくとも一つのコンポーネントが正しく動作する必要があります。システムには、直列および並列で配置されたコンポーネントを両方、格納することもできます。RBD を直列、並列または直並列に減らすことができない場合、それは複雑なシステムであると見なされます。
本論文では、複雑なシステムの信頼性を示す厳密解析式の生成を扱います。ここで示された手法は、有向非巡回グラフ (すなわち RBD) で始点と終点のすべてのパスを検索すること、および確率の包除原理に依存します。
本論文で報告した時間は、組込関数 Timing を使用してカスタム・ワークステーション PC 上で測定されました。システム構成は Intel® Core™ i7 CPU 950 @ 4 GHz および 24 GB の DDR3 メモリです。Microsoft® Windows™7 Professional (64-bit) で動作し、および MathematicaMark9 ベンチマークでスコア 1.32 となっています。
有向グラフ、G = (V, E) (頂点の有限集合 と有向辺と呼ばれる頂点の順序対の有限集合 E から成る) を検討することから開始します。組込関数 Graph は、頂点および辺の明示的リストからグラフを作成するために使用することができます。

G 4,4 とラベル付けされた、この2次元グリッドグラフは、組込関数 GridGraph を使用すると、さらに効率的に作図することができます。本セクションでは、この関数を使用して説明します。
ここで頂点 v ∈ V について、外近傍の集合 N+G(v) を
として定義します。
なおここで v w は、v から w への有向辺を意味するものとします。これは、関数 VertexOutNeighbors 内で実装されます。

VertexOutNeighbors は、組込関数 VertexOutDegree に似た振る舞いをします。グラフ G および頂点 v を与えると、関数は指定された頂点における外近傍のリストを返します。
ただし、グラフ G のみを指定すると、関数はグラフ内のすべての頂点の外近傍の頂点のリストを返します。

外近傍に表示される順序は、VertexList によって返される頂点の順序で決まります。
単純に ![]() を
を ![]() に変更するだけで、内近傍の N–G(v) を得る類似関数を実装することができます。
に変更するだけで、内近傍の N–G(v) を得る類似関数を実装することができます。
次はグラフ横断の手法を検討します。グラフのすべての頂点に系統的にアクセスする一般的な手法の一つに、深さ優先検索 (DFS) があります。基本的に、DFS アルゴリズムは頂点の探索を行い「訪問済み」の印をつけた後、それらのすべての近傍を再帰的に訪問します [2]。関数 DepthFirstSearch は、有向グラフに対してこのアルゴリズムを実装します。
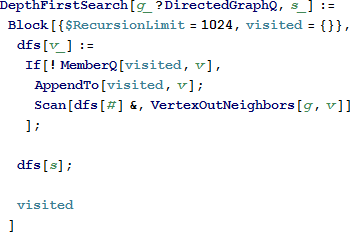
グラフ G および、始点を示す頂点 s を与えると、DepthFirstSearch は訪問した順序で頂点のリストを返します。
組込関数 DepthFirstScan の結果とこれを比較します。

次に、関数 DirectedAcyclicGraphQ を定義します。
グラフ G が有向および非巡回の両方である場合、DirectedAcyclicGraphQ は True を返します。そうでない場合は False を返します。
最後に、有向非巡回グラフ G 内で、ふたつの任意の頂点 s, t ∈ V 間のすべてのパスを探索する場合の問題について検討します。一般的に、s はソース、t はターゲットと呼びます。G におけるパスは、i = 1, 2 , … , k -1 に対する ![]() のような頂点の配列
のような頂点の配列 ![]() として定義されます。有向非巡回グラフに制限したため、パスはすべて単純であり、すべてのパスの頂点がはっきりと区別されます。
として定義されます。有向非巡回グラフに制限したため、パスはすべて単純であり、すべてのパスの頂点がはっきりと区別されます。
深さ優先探索アルゴリズムを部分的に変更して解を得ることにします。
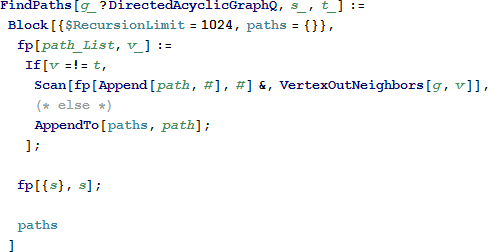
オリジナルの DFS アルゴリズムのように、頂点を訪問したらすべての近傍を再帰的に訪問しますが、頂点に「訪問済み」の印がつけられているかを確認するのではなく、現在の頂点とターゲットを比較します。それらが一致しない場合はグラフの横断を続けます。そうでない場合はターゲットに到達して、後の出力のためにパスを保存します。
有向非巡回グラフ G、ソースの頂点 s、ターゲットの頂点 t を与えると、FindPaths は s と t をつなぐすべてのパスのリストを返します。

この例の場合、関数が結果を返すのに約 0.85 ミリ秒かかります。
FindPaths は、あらゆる頂点のペアに対して動作します。
パスが見つからなかった場合、関数は空のリストを返します。
ここまで、抽象的で数学的な意味でグラフの検討を行いました。以降では、システム内のコンポーネントと頂点および、それらの関係と辺を結びつけて、有向巡回グラフから信頼性ブロック図 (RBD) の推移を検討します。
RBD 内の単一成分を検討します。ソースからコンポーネントを通りターゲットに移動する「フロー」を想像します。このフローをスムーズに流すことができれば、コンポーネントが機能していると見なすことができます。コンポーネントが機能していない場合は、フローはターゲットに到達することができません。
「フロー」の概念は、システム全体に拡張することができます。ソースからターゲットへのフローを許す機能をする一連のコンポーネントが存在すれば、システムが機能していると考えることができます。RBD 内のパスを、システムが機能していることを保証する一連の機能コンポーネントとして定義します。システムの RBD の表示に有向非巡回グラフの使用したため、パスはすべてミニマルです。換言すれば、パス内のすべてのコンポーネントは明確に区別することができます。
システムの RBD のミニマルパスが得られると、確率の包除原理を信頼性解析の厳密式の生成に利用することができます。{A1, A2, …, An} をシステムにおけるすべてのミニマルパスの集合であるとします。システムを機能させるためには、少なくとも一つはミニマルパスが機能しなければなりません。システムの信頼性 RS を、すべてのミニマルパスの和集合の確率として記述することができます。
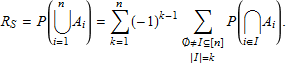
これは、関数 SystemReliability 内で実装されます。

有向非巡回グラフ G で示される RBD において、ソースの頂点 s とターゲットの頂点 t を与えると SystemReliability は、信頼性の厳密解析式を返します。
4つのコンポーネントからなる直列配置の単純なシステムの RBD を検討します。
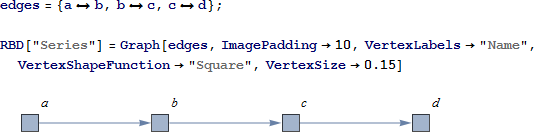
システムの信頼性は、4つのコンポーネントの値から与えられます。
4つのコンポーネントからなる並列配置の単純なシステムの RBD を検討します。
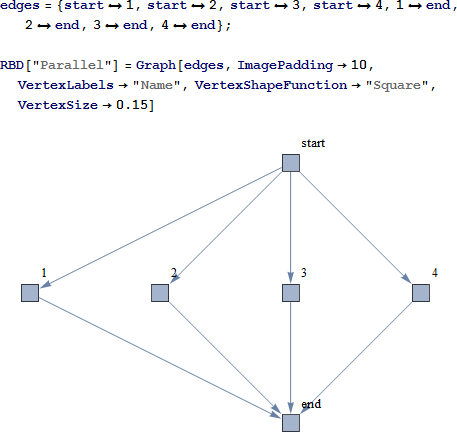
コンポーネント「start」と「end」は実際のシステムの一部ではありません。これらは、RBD が有向非巡回グラフの基準に合うことを保障するために追加されています。
さらに、これらの実在しないコンポーネントは完全な信頼性を有すると解釈して、つまり、R = 1 であると考えます。これらはシステムの信頼性には影響を及ぼさないため、解析式の結果から安全に削除することができます。方法としては、置換規則のリストを定義して SystemReliability の結果に適用します。
システムの信頼性は、4つのコンポーネントの値から与えられます。
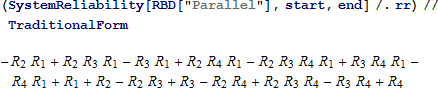
次は4つのコンポーネントからなる直並列の2つの単純なシステムの RBD を検討します。
システム 1

コンポーネント c は、コンポーネント a と直列で、両コンポーネントはコンポーネント b とは並列です。

システム 2
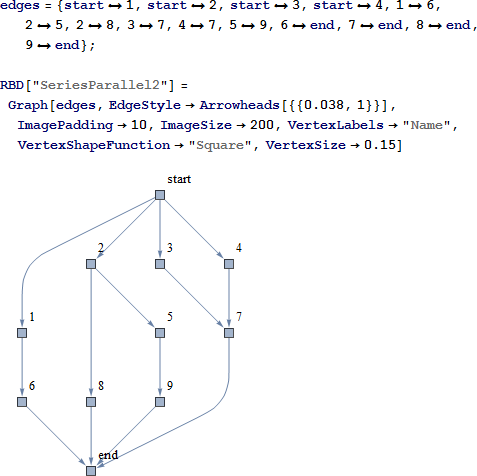
前の例のように SystemReliability を使用して、信頼性の厳密解析式を得ます。

最後に、2つの複雑なシステムの RBD を検討します。
システム 1
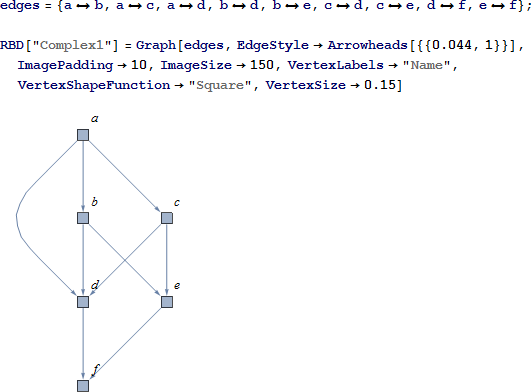
システムの信頼性は、6つのコンポーネントの値から与えられます。
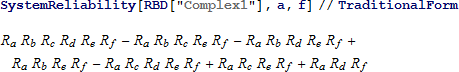
結果は約 0.59 ミリ秒後に返されます。
システム 2
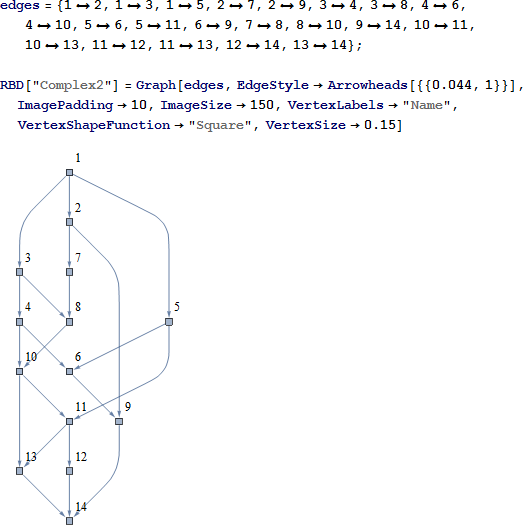
システムの信頼性は、14 のコンポーネントの信頼性の値から与えられます。
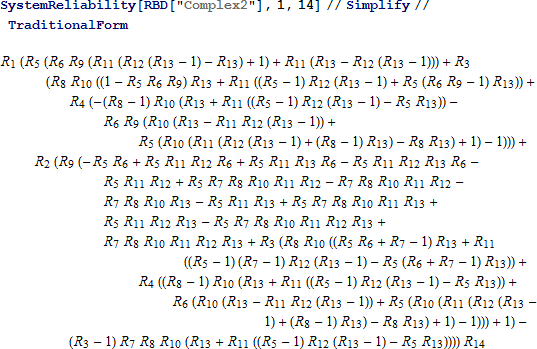
結果は約 0.33 秒後に返されます。
以降では、信頼性ブロック図に格納された情報を基に、複雑なシステムの信頼性を経時的式を導出することについて検討します。
6つのサブシステムで構成される一般的なシステムがあり、それらの間の信頼性が分かっていると仮定しましょう。さらに、内在する統計的分布および、システムの信頼性モデルに使用されるパラメータが分かっているとします。
システムの RBD を作成することから開始します。

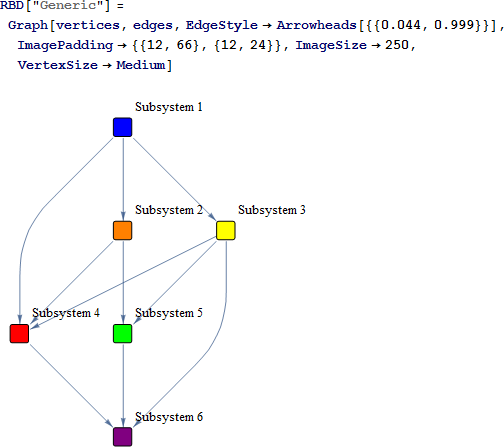
RBDを定義するとき、Property 関数を使用して各サブシステムに関連付けられた情報を格納しました。例えば、カスタムプロパティ "Distribution" は、パラメトリック統計的分布を格納するために使用します。ラベル、イメージおよび他のプロパティも指定することができます。
次に SystemReliability を使用して、信頼性の厳密解析式を生成します。
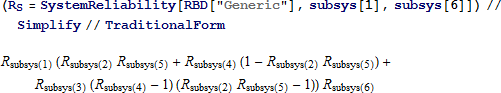
i 番目のサブシステムの信頼性関数は次の式で与えられます。
ここで、Fi(t) は対応する累積分布関数 (CDF) となります。各サブシステムに PropertyValue を使用して RBD 内に格納されたシンボリックの分布を抽出し、次に、組込み関数 CDF を使用して信頼性関数を作成します。

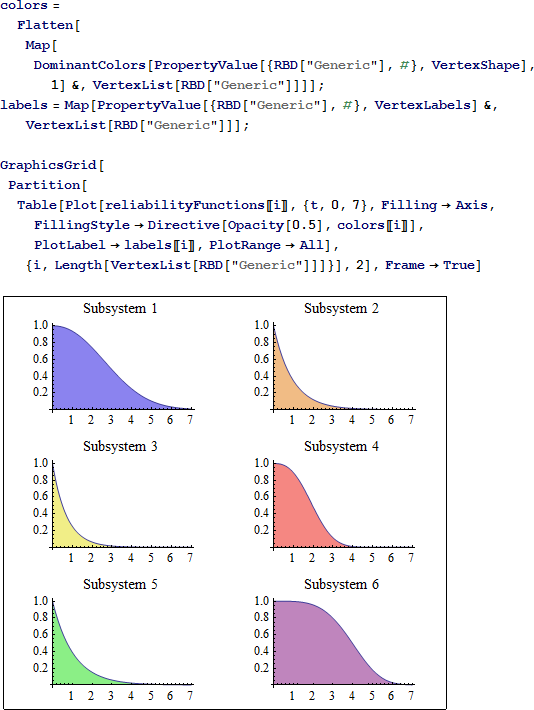
追加情報 (例えば、サブシステムのラベルなど) を RBD から抽出して信頼性関数と組み合わせ、比較用のプロットを作成します。
統計解析式を経時的関数に変換するために、まず、置換規則のリストを定義します。

次に、システム信頼性の式に規則のリストを適用します。
結果は、RBD によって記述された複雑なシステムの経時的信頼性関数となります。
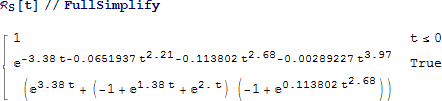
最後に、システムの経時的信頼性のプロットを作成します。
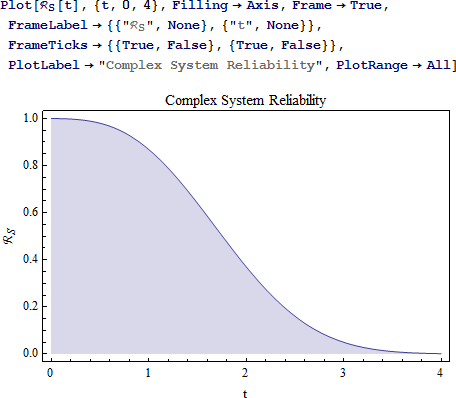
有向非巡回グラフを使用してシステムの信頼性ブロック図を示し、複雑なシステムの信頼性の厳密解析式を生成する方法を実証しました。さらに、RBD に格納された統計的情報を基に、システムの信頼性の解析式を経時的関数に変換する方法を示しました。また、複雑なシステムの解析に着目する一方で、パス検索の組み合わせ、包除原理が、直列の単純システム、並列、または、直並列配置にも同じように当てはまることも示しました。
静的な解析式やシステムの経時的な解が分かると、さらに高度な信頼性の解析が可能になります。例えば SystemReliability の結果を使用して、i 番目のコンポーネントの Birnbaum 重要度
を簡単に計算することができます。同様に、システムの経時的信頼性関数から、ハザード関数や故障率を導くこともできます。
本論文で示した機能を向上、拡張するにはいくつかの方法があります。
SystemReliability の効率を向上する最終的にコードは完全なドキュメンテーションを持つユーザーフレンドリーなパッケージにまとめることが可能です。
T. Silvestri, “Complex System Reliability,” The Mathematica Journal, 2014. doi:10.3888/tmj.16-7.
Todd Silverstri は、2001年にシカゴ大学より物理学と数学の学士号を取得。大学院生のときにトーマス・ジェファーソン加速機研究所 (TJNAF) に短期間勤務し、高運動量移行時の因子から中性子電気を測定する実験で使用する中性子検出器の構築および検証に協力しました。2006年~2011年まで、米軍武器工学技術センター (ARDEC) に物理学者として勤務。ARDEC では軍事システムの信頼性の向上に焦点を合わせた小さな研究室を設立し、主任研究員を務めました。現在はいくつかの個人プロジェクトに従事しています。