| 本アーティクルは The Mathematica Journal (volume 16, 2014) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 16, 2014) and the copyright holder is Wolfram Research, Inc." |
本アーティクルは、言語の間のモルフィズムの繰り返しで発生する可能性があるフィボナッチ列および一般化のいくつかの組み合わせ属性を実装します。フラクタル曲線のいくつかのグラフィックス属性は、このワードと関連しています。曲線はLシステムで使用されるものと似た描画規則から生成されます。プログラムへの簡単な変更で、他の面白い曲線を生成できます。
無限のフィボナッチ列は、明らかに、ワードの組み合わせ論の分野 [1-4] の中で最も研究されたワードの１つです。
これは Sturmian 列の原型です [5]。ワード f は、組み合わせ属性 [6-7] を持つフラクタル曲線に関係します。
この論文では、f と 描画規則から曲線を生成する Mathematica プログラムを実装します。これらの規則は、L システムで使用されるものと似ています。
この論文の概要は次のとおりです。第２節は、ワードの組み合わせ論のいくつかの定義と考え方を示します。第３節は、フィボナッチ列、フラクタル曲線およびフィボナッチ列フラクタルに制限されているワードのファミリーを紹介します。最後に、第４節で、フィボナッチ列とそのフィボナッチ列フラクタルを一般化します。
用語と表記は、主に [5] および [8] のものを使用しています。Σ を有限アルファベットとします。その要素はシンボルと呼ばれます。Σ 上のワードは、Σ からのシンボルの有限シーケンスです。Σ 上のすべてのワードのセットは、つまり、Σ によって生成された自由モノイドは、Σ* によって示されます。Σ のアイデンティティ要素 ε は空のワードと呼ばれます。いかなるワード w ∈ Σ* に対しても、|w| は長さ、つまり、w に発生するシンボル数です。ε の長さは、ゼロであると認識されます。 a ∈ Σ と w ∈ Σ* の場合、|w|a は、w 内の a の発生数を示します。
Σ* 内の２つのワード u = a1a2 … ak および v = b1b2 … bs に対して、2つのワードの連結は、uv によって示され、uv = a1a2 … akb1b2 … bs となります。v = ε の場合、uε = εu = u となり、さらに、un によってワード uu … u（u 回）を意味します。ワード v は、もし、u = xvy のような x, y ∈ Σ* が存在する場合、u の部分ワード（または因子）です。x = ε の場合、u = vy であり、v は u の接頭辞と呼ばれます。y = ε の場合、u = xv であり、v は u の接尾辞と呼ばれます。
ワード u = a1a2 … ak の反転は、ワード uR = akak-1 … a1 で、εR = ε です。ワード u は、uR = uの場合、パリンドローム（回文）です。
Σ 上の無限ワードは、マップ 
で、u = a1a2a3 … のように記述します。Σ 上のすべての無限ワードのセットは、Σω によって示されます。
n が素数のとき pn = 1、 そうでないとき pn = 0 のようなワード p = (pn){n≥1} = =0110101000101 … は、無限ワードの例です。ワード p は、素数の特性シーケンスと呼ばれます。ここに、p の最初の 50 個があります。
Σ と Δ をアルファベットにします。モルフィズムは、すべての x, y ∈ Σ*、h(x y) = h(x)h(y) に対して、マップ h:Σ* → Δ* です。
多くの顕著な属性をもった特別なクラスのワードがあります。いわゆる Sturmian 列です。これらのワードはいくつかの同等の定義（例えば [5] [8] を参照）を持ちます。
w ∈ Σω とします。P(w, n) は、w の複雑性関数で、すべての整数 n ≥ 0 に対して、w 内の長さ n の部分ワードの数をカウントするマップです。無限ワード w は、すべての整数 n ≥ 0 に対し、P(w, n) = n + 1 の場合、Sturmian 列です。
例えば、P(01101010001010,5) = 9 です。
いかなる Sturmian 列に対しても P(w, 1) = 2 であるため、Sturmian 列は、２つ以上のシンボルでなければなりません。例１でのワード p は、P(p, 2) = 4 ≠ 3であるため、Sturmian 列ではありません。
2つの実数 α, β ∈ 
(α は無理数) と 0 < α < 1、0 ≤ β < 1を与え、無限ワード w = w1w2w3 … を wn = ⌊(n+1)α + β⌋ – ⌊nα + β⌋ として定義します。それぞれ、α と β は、傾きおよび切片です。このワードは、機械的であると言われます。機械的なワードは、Sturmian 列と同等です [5]。特別な場合として、β = 0 は特徴的なワードを与えます。
α を無理数とし、0 < α < 1 とします。 n ≥ 1 に対して、wα(n) = ⌊(n+1)α⌋ – ⌊nα⌋ と w(α) = wα(1)wα(2)wα(3) … を定義します。w(α) は傾き α をもつ特徴的なワードと呼ばれます。
一方で、各 ai が正の整数の場合、すべての無理数 α ∈ (0, 1) がユニークな連続分数展開を持つことに注意してください。
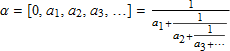
α = [0, 1+d1, d2, …] を d1 ≥ 0、n > 1 に対して dn > 0 であるような無理数とします。ディレクティブシーケンス (d1, d2, … dn, …) に対し、s-1 = 1、s0 = 0、sn = sn-1dnsn-2、n ≥ 1 によって定義されるワードのシーケンス (sn){n≥-1} を関連付けます。
このようなワードのシーケンスは、標準シーケンスと呼ばれます。このシーケンスは、次の方法で特徴的なワードに関連づけられます。任意の n ≥ 0 に対して、sn は sn+1 の接頭辞であると観察されます。これは無限ワードとして limn→∞ sn に意味を与えます。実際、各 sn がすべての n ≥ 0 と w(α) = limn→∞ に対する接頭辞であることを証明できます [5]。
フィボナッチ列は、次のように帰納的に定義される {0, 1} のワードです： f0 = 1、f1 =0 、n ≥ 2 に対して fn = fn-1 fn-2 。ワード fn は有限のフィボナッチ列として参照されます。極限は、
フィボナッチ列と呼ばれます。
Fn が nthフィボナッチ数である場合、|fn| = Fnであることは明確です。フィボナッチ数 Fn が n ≥ 2 であるすべての整数に対し、初期値 F0 = F1 = 1 を持ち再帰的関係 Fn = Fn-1 + Fn-2 によって定義されていることを思い出してください。無限のフィボナッチ列 f は、Sturmian 列です [5]。正確に 
で、
は黄金比です。
ここに、f の最初の 50 個を並べてみます。
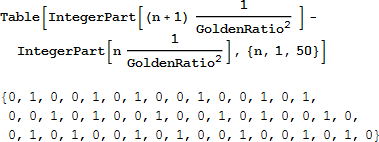
フィボナッチモルフィズム σ: {0, 1}* → {0, 1}* は、σ (0) = 01 と σ (1) = 0 によって定義されます。
フィボナッチ列 f は、すべての n ≥ 1 に対し、 f = lim n→∞ σn(1) と σn(1) = fn を満たします。
最初の 9 個の有限のフィボナッチ列を表示します。
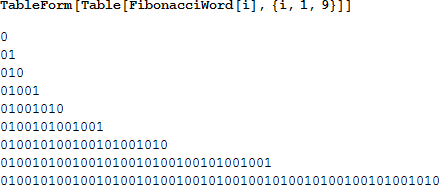
Φ:{0,1}* → {0, 1}* を Φ が最後の２つのシンボルを削除するようなマップとします。
次の命題は、フィボナッチ列についてのいくつかの基本的な性質を要約しています。
フィボナッチ列と有限のフィボナッチ列は以下を満たします：
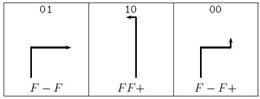
フィボナッチ列は、描画ルールを使用して曲線に表現することができます。特定の操作が、シンボル読み取り（これはLシステム [9] の中で使用されるものと同じ考え）に続きます。この場合では、描画規則は「奇数偶数描画規則 (the odd-even drawing rule)」と呼ばれます [7]。
| symbol | position of symbol | Draw a line forward, then |
|---|---|---|
| 1 | any | stay straight |
| 0 | even | turn left |
| 0 | odd | turn right |
で示される nthフィボナッチ曲線は、ワード fn に奇数偶数描画規則を適用した結果です。フィボナッチ列フラクタルは
として定義されます。
L システムを生成するために、プログラム LShow を [10] を基に作成します。
図1は、奇数偶数描画規則の L システムの解釈を示します。
 |
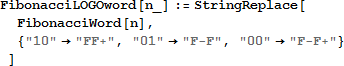
ここに、n = 9, …, 21 に対する曲線 があります。
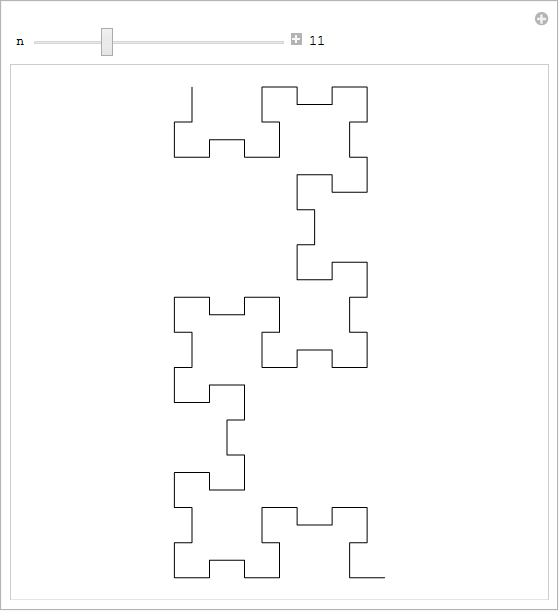
曲線 と 
の属性についての次の命題は、命題1のフィボナッチ列の特性から、直接導かれます。その他の特性は、[7] で見ることができます。
フィボナッチ列フラクタル と曲線 は、以下の属性を持ちます：
は長さ 1 または 2 のセグメントだけから成る のターンの数は、フィボナッチ数 Fn-1 である は曲線 n-3 に似ている は対称である は、5つの曲線 = n-3 n-3 n-6 ‘n-3 ‘ n-3 からなる。‘ n は、ワード l n に奇数偶数描画規則を適用した結果である次の図は曲線 17 および５つの曲線 17 = 14 14 11 ‘14 ‘14 を示します。
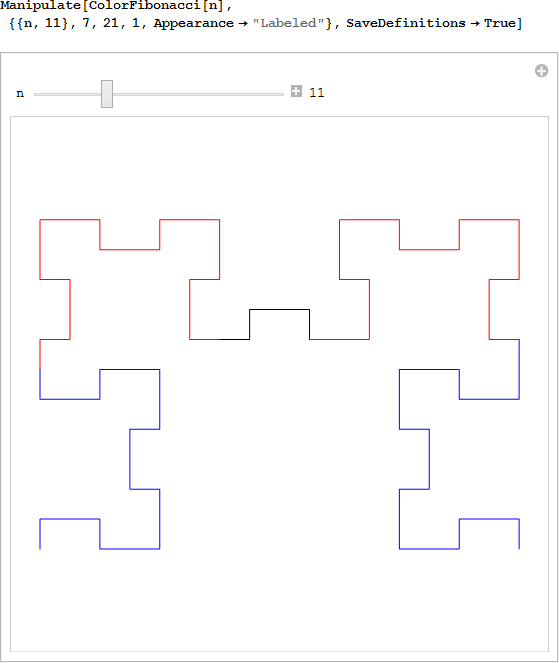
フィボナッチ列および他のワードは、[7] で導入した密度の高いフィボナッチ列から導くことができます。
密度の高いフィボナッチ列 
は、モルフィズムを適用することによって、フィボナッチ列 f から導かれます。
つまり、 = 102210221102110211022102211021 …
描画規則を考慮すると、全体の角度は、規則を適用したワードによって生成される連続角度の合計になります。自然な描画規則によると、Δ(1) = – π/2、Δ(0) = 0 、Δ(2) = π/2 であり、Δ(120) = Δ(1) + Δ(2) + Δ(0) = 0 となります。
描画規則に対して、ワード d の出力の角度は全体の角度を与える関数 Δ となります。モルフィズム θ は、任意のワード w に対して Δ(θ(w)) = Δ(w) である場合、出力の角度を保持します。さらに、モルフィズム θ が、任意のワード w に対して Δ(θ(w)) = –Δ(w) である場合、出力の角度を反転します。
密度の高いフィボナッチ列が、強くフィボナッチ列フラクタルにつながるのは、 がフィボナッチ列フラクタルに制限されている一群の曲線の全体を生成することができるためです [7]。必要とされる全ては、 に出力の角度を保存、または反転するモルフィズムを適用することです。
例をいくつか挙げてみます。
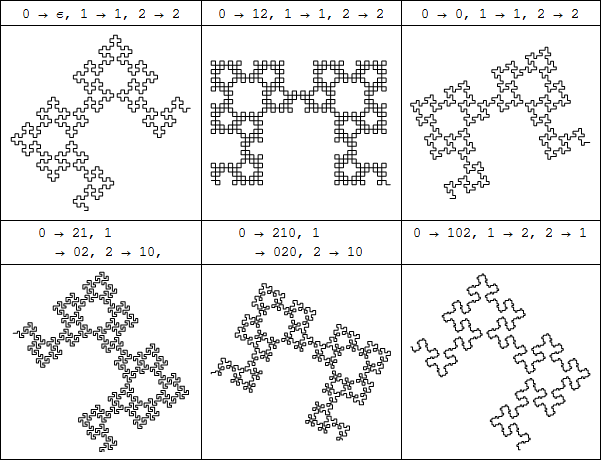
他の角度を持つ別の例です。
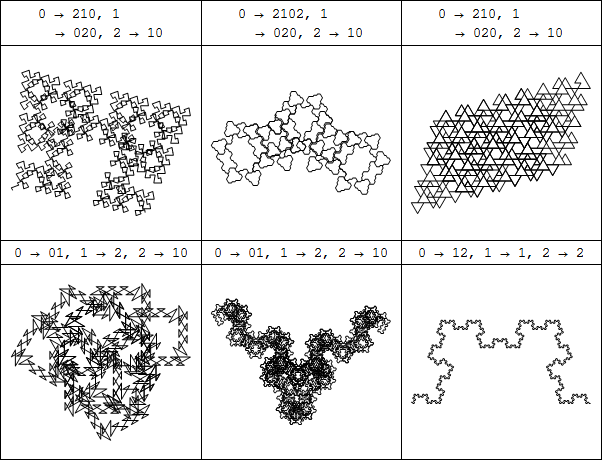
ここではフィボナッチ列とフィボナッチ列フラクタルの一般化を導入します [11]。
(n, i)-フィボナッチ列は、n ≥ 2 と i ≥ 2 に対して、f0[i] = 0、f1[i] = 0i-1、fn[i] = fn-1[i] fn-2[i] fn-2[i] によって誘導的に定義された {0, 1} 上のワードです。無限ワード
f[i] = lim n→∞ fn[i]
は、i-フィボナッチ列と呼ばれます。
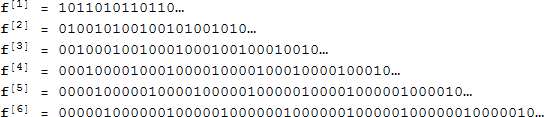
2-フィボナッチ列は、古典的フィボナッチ列です。次は、最初の 6つの i -フィボナッチ列です。
次の命題は、フィボナッチ列 f を f[i] に関連付けます。
φi:{0, 1}* → {0, 1}* を φi(0) = 0 と φi(1) = 0i 1, i ≥ 0 によって定義されるモルフィズムとします。すると、すべての i ≥ 0 に対して、
となります。
(n, i)-フィボナッチ数 Fn[i] は、すべての n ≥ 2 と i ≥ 1 に対して、F0[i] = 1、F1[i] = i 、Fn[i] = Fn-1[i] + Fn-2[i] によって再帰的に定義されます。
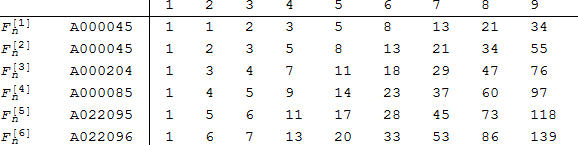
(n, 1)-フィボナッチ数はフィボナッチ数列であり、(n, 2)-フィボナッチ数は、1 シフトしたフィボナッチ数です。配列次の表は、シーケンス Fn[i] の最初のラウンドとオンライン百科事典シーケンス（OIES）の参照番号を示します [12]。
i-フィボナッチ列および (n, i)-フィボナッチ列は、次を満たします：
α = 
を無理数で、i を正の整数とすると、w(α) ＝ f[i] です。
証明については、[11] を参照してください。この定理は i -フィボナッチ列が Sturmian 列であることを暗示しています。
φ が黄金比で、
であることに注意してください。
n[i] で示される (n, i)th-フィボナッチ曲線は、ワード fn[i] に奇数偶数描画規則を適用した結果です。i -フィボナッチ列フラクタル [i] は
として定義されます。
次は i = 2,3,4,5,6,7 に対する曲線 n[i] です。
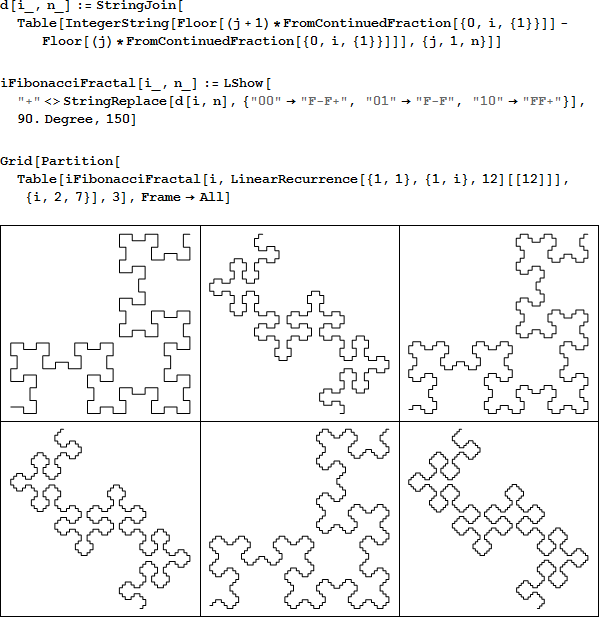
i -フィボナッチ列フラクタルおよび曲線 n[i] は、以下の属性を持ちます。
[i] は、長さ 1 または 2 のセグメントだけから構成されるn[i] は曲線 n-3[i] に似ているn[i] は、5つの曲線 n[i]=n-3[i]n-3[i]n-6[i]‘n-3[i]‘n-3[i]からなるn[i] は対称であるn[i] と n-3[i] の間のスケールファクターは 
である
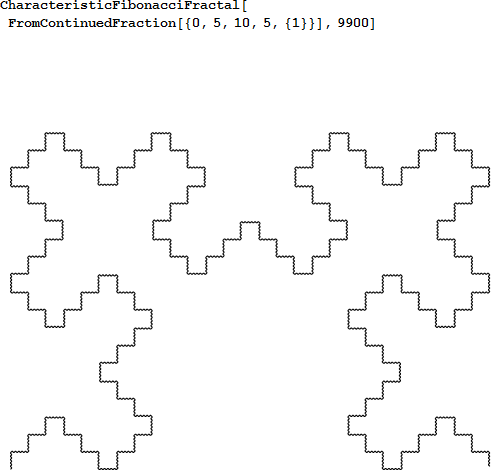
ここでは、特徴的なワードから新しい曲線を生成するために、これまでのアイデアを適用します（定義３参照）。
の場合、曲線は、フィボナッチ列フラクタルパターンを示します。
７つ例を挙げてみます。
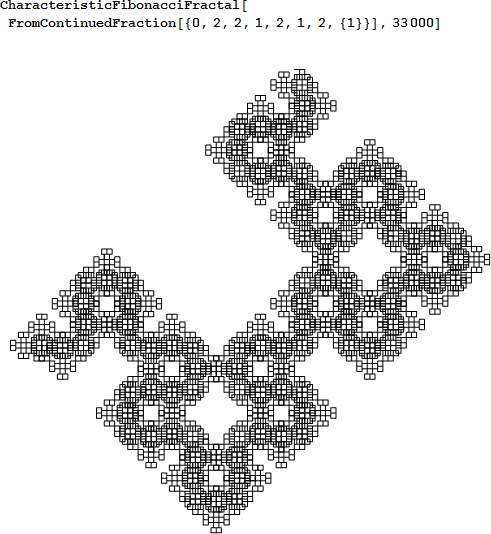
最初の著者は、部分的に認可番号 USA-II-2012-14 の下で Universidad Sergio Arboleda によってサポートされています。著者は、この記事を書くにあたり、Ljubljana University の Borut Jurčič-Zlobec に感謝したい。
J. L. Ramírez and G. N. Rubiano, "Properties and Generalizations of the Fibonacci Word Fractal," The Mathematica Journal, 2014. doi:10.3888/tmj.16-2.