| 本アーティクルは The Mathematica Journal (volume 15, 2013) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 15, 2013) and the copyright holder is Wolfram Research, Inc." |
負の二項回帰は、最尤法を用いて構築されます。従来のモデル (traditional model) とオフセットを用いた比率モデル (rate model) について、回帰診断とともに紹介します。
負の二項回帰は、従属変数 Y がイベントが発生した回数のカウントである一般化線形モデルの一種です。負の二項分布の便利なパラメータは Hilbe [1] によって与えられます:
ここで μ(μ > 0)は Y の平均値で、α(α > 0)は不均一(heterogeneity)パラメータです。Hilbe [1] によると、ポアソン-ガンマ混合、もしくは、1/α 回の成功をする前の失敗した回数として、このパラメータは導出されており、1/α は整数である必要はありません。
文献 [1] で NB2 モデルと称される従来の負の二項回帰のモデルは、
であり、予測変数 x1, x2, … , xp が与えたときの、母回帰係数 β0, β1, β2, … , βp を推定します。
n 個のランダムサンプルが与えられると、サンプル i について従属変数 yi と予測変数 x1i, x2i, … , xpi が得られます。ベクトルと行列表記を用いて、β = (β0 β1 β2 … βp)T とし、また予測変量を次の計画行列 X のように整理することができます。
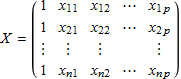
i 行目の X を xi とし、式 (2) の指数を取ると、式 (1) の分布を次のように書くことができます。
最尤法を用いて α と β を推定します。尤度関数は
となり、対数尤度関数は
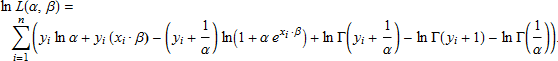
となります。ln L(α, β) を最大にすると α と β の値は求める最尤推定量になるでしょう。そして推定量の推定分散-共分散行列は Σ = –H -1 です。ここで は対数尤度関数の二次導関数のヘッセ行列です。そして分散-共分散行列は Wald 信頼区間と係数推定量の p-値を求めるのに使うことができます。
私たちは Hilbe [1] (R と Stata を使っている) によって与えられるいくつかの例を再現するために Mathematica を使います。私たちは既知の回帰係数から生成されたシミュレートデータを用いて始め、最尤法を用いて係数を求めます。平均が、p=2, α = 0.50, β =(2.00 .75 -1.25)T を用いた式 (2) によって与えられる負の二項分布を持つ従属確率変数 Y の n = 5000 の観測のサンプルを生成します。計画行列 X1 は独立標準正規変量を含みます。

ここで、対数尤度関数 (3) を定義し最大値を求め、α と β の値を得ます。初期値を調べるために何回か試行が必要かもしれません。また目標とする精度 (accuracy) は低くする必要があるかもしれません;α が通常 0.0 から 4.0 のとき、GeneralizedLinearModelFit 関数によるポアソン回帰を用いることで、β の良い初期値を得ることができるでしょう。

しかし、意図的に全ての初期値を 1.0 に設定しても、うまく正しい推定量を見つけることができます。

二つの役立つ関数を定義します。

次に、推定量の標準誤差を求めます。標準誤差は上述したように Σ = –H -1 で与えられる分散共分散行列 Σ の対角要素の平方根です。ここで H は対数尤度関数の二次導関数のヘッセ行列です。まず、ヘッセ行列を定義します。
そして、パラメータ推定量の値からヘッセ行列と Σ を求めます。
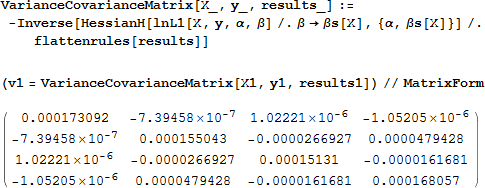
最後に、これが標準誤差です。

係数の推定量、標準誤差、Wald z 統計量、p 値、信頼区間といった結果をテーブルで表示することができます。

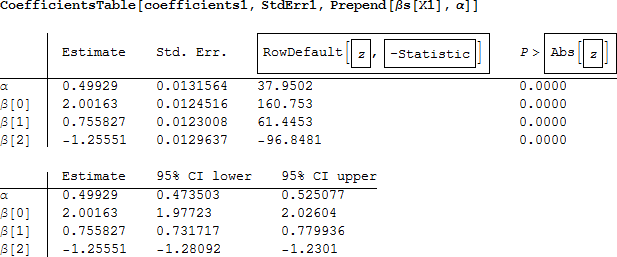
それぞれの係数の信頼区間に母パラメータが収まっていることが分かります。
従属変数 Y が一定の時間 t の間のイベントの回数を数える場合、観測率 Y /t は、少しの調整で上記の従来の負の二項分布のモデルによってモデル化することが出来ます。Y /t を比率であると解釈すると、t は部分母集団のサイズか領域であると考えることができることに気づきます。
E (Y /t) = μ /t なので、上記の式 (2) のモデルを次のように調整します。
これは次のようにも書くことができます:
この最後の項 ln t はオフセット (offset) と呼ばれます。したがって対数尤度関数では、μ を exi・β と替える代わりに exi・β+ln t と替えることで、次の結果を得ることができます。
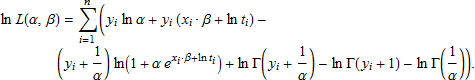
その後は、前と同じように進め、パラメータを推定するために、新しい対数尤度関数の最大値を求めます。
文献 [2] から利用でき、文献 [1] では R と Stata を用いて解析されている、乗組員を削除したタイタニックの生存者のデータは、Table 1 のように整理できます。
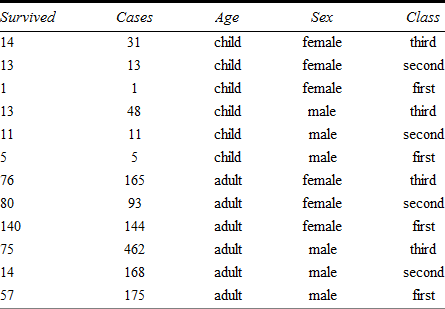 |
何故生き残った1等船室の子供は2等船室や3等船室より少ないのでしょうか?1等船室の子供は余分な危険にさらされていたからですか?いいえ、そもそもタイタニックに1等船室のの子供はそもそも少ししかいなかったからです。ですから、生存者の実数 (Y) をモデル化すべきではありません。代わりに生存率である生存者の割合 (Y / cases) をモデル化すべきです。そこで式 (4) において cases の数 t が必要となります。
計画行列を準備しましょう。大人と男性 1 で示し、そして、2等船室と3等船室のために指示変数を用います。これは1等船室がリファレンスになっていることを意味します。

次に、従属変数と offset を準備します。
対数尤度関数は式 (5) のように定義します。
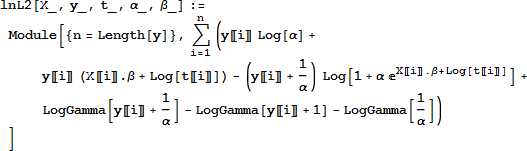
まず、係数を求めるためにその最大値を求めます。

次に、係数の標準誤差を求めます。

そして、再び結果をテーブルで表示します。
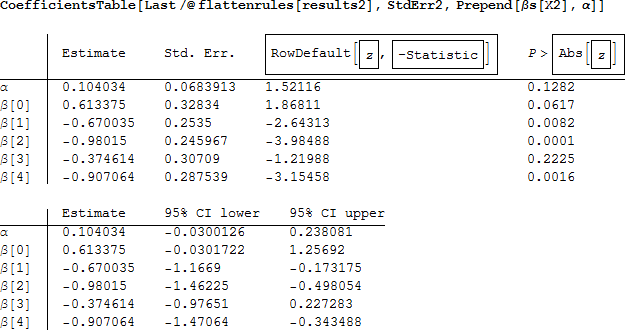
しかし、おそらくさらに役立つ係数の解釈は、それぞれの係数の指数で得られる変数の発生割合比 (IRR) です。 例えば、t 人の大人のサンプルから、その生存率はモデル式 (4) より、μ adults / t = exp(β0 + β1(1) + β2(sex) +β2(class2) +β3(class3)) となります。一方、t 人の子供の生存率は μchildren / t = exp(β0 + β1(0) + β2(sex) +β2(class2) +β3(class3)) となります。 そして、2つの割合を割ることによって、割合比 (IRR) は
であり、その値は e -0.670034 = 0.51 であると推定されます。このように、同じ性別と船室の間で、大人は生存の割合は子供のおおよそ半分であると解釈することができます。IRR の標準誤差は係数の標準誤差と推定された IRR を乗じることによって求められます(文献 [1])。一方、係数の信頼区間の指数をとることによって、IRR のための信頼区間が求められます。
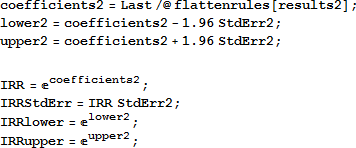
α や β0 の IRR は必要ありません。そこでそれらを取り除き、結果をテーブルで表示します。
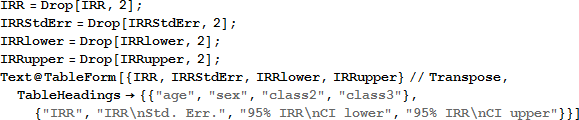
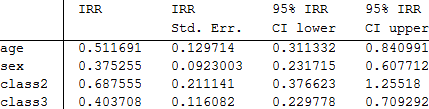
class2 変数の信頼区間は、1.0 を含んでおり、その係数が有意でないことと一致します。そして、2等船室の乗客の生存率と1等船室の乗客の生存率とに有意な差は見られません。このことについては、いくつかのモデル評価統計量と残差の計算の後に話をします。
さまざまなモデルフィット統計量と残差を計算することができます。ここでは文献 [1] で与えられた定義を使います (異なる定義も存在しますが、軽微な変更で対応できるでしょう) 。
一般に使用されるモデルフィット統計量は、対数尤度、デビアンス、ピアソンカイ二乗分布、赤池情報量規準 (AIC)、ベイズ情報量規準 (BIC) です。
対数尤度 ℒ は、最大化の過程の副産物として既に得られています。デビアンス D は次のように定義されます
ここで ℒ (μi; yi) は対数尤度関数 (5) であり、ℒ (yi; yi) は μi を yi に置き換えた対数尤度関数です。NB2 モデルのために、![]() とすることにします。ここで、
とすることにします。ここで、
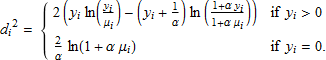
です。ピアソンカイ二乗分散統計量は ![]() で与えられ、また、AIC と BIC は次のように定義されます。
で与えられ、また、AIC と BIC は次のように定義されます。
および
上記のタイタニックのデータについて計算し、表示します。
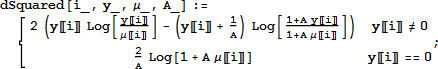

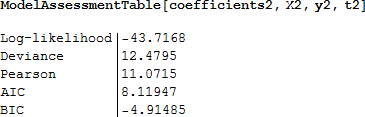
これらのモデル評価統計量は、競合するモデルとの比較に役立ちます。他のモデルとの比較については、残差を計算した後の次のセクションで続けます。
通常の残差はもちろん yi – μi です。一方、式 (6) で定義されるようにピアソン残差は ![]() 、デビアンス残差は
、デビアンス残差は ![]() です。
です。
これらの残差は ![]() で割ることにより標準化することができます。ここで hi はハット行列 W 1/2 X (X ‘ W X)-1 X‘ W 1/2 から得られるてこ比です。W は i 番目の対角成分が μi /(1+α μi) の n×n 対角行列です。
で割ることにより標準化することができます。ここで hi はハット行列 W 1/2 X (X ‘ W X)-1 X‘ W 1/2 から得られるてこ比です。W は i 番目の対角成分が μi /(1+α μi) の n×n 対角行列です。
タイタニックのデータの非標準化残差は次のようになります。


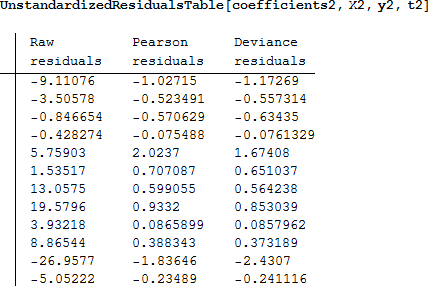
そして、これがてこ比と標準化された残差です。


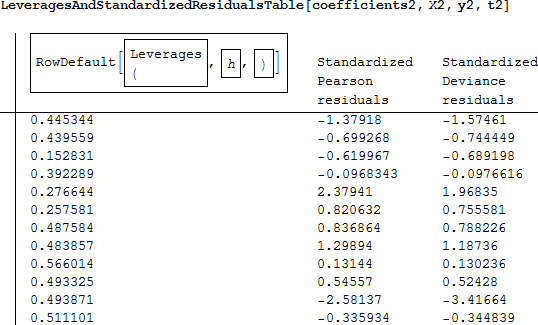
Hilbe は、てこ比が高いときは h に対して標準化されたピアソン残差をプロットすることを勧めています。もし、-2 ~ +2 の外側に残差がプロットされると、そのモデルが適切でないことがプロットからわかります。
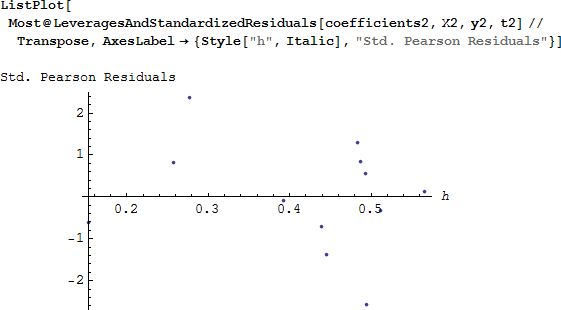
-2 ~ +2 の範囲にない標準化されたピアソン残差は2点あり、その1つのてこ比は高い値となっています。変数 class2 が有意でなかったことを思い出してください。おそらく class2 を取り除けば、そのモデルは改善するかもしれません。 必要なのは、計画行列 から class2 を削除し、最大化するコマンドから対応する初期値を削除し、再びモデルを実行することです。class2 を削除したモデルから評価統計量と標準化された残差を計算します。
まず、計画行列 X を準備し、係数を求めます。


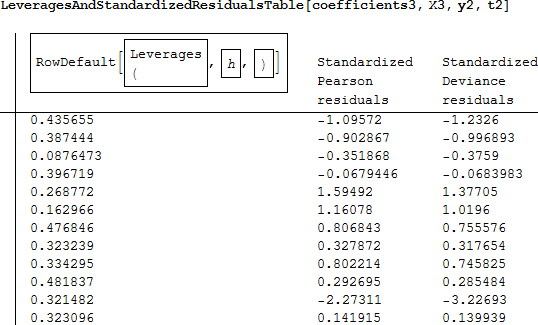
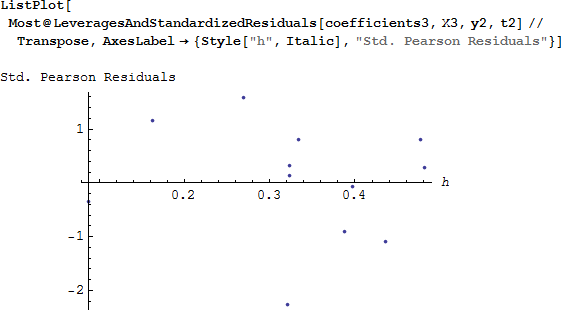
すべてを含めたフルモデルと比較すると、評価統計量は改善されています (それはとても小さく、良いフィットであることを示しています)。そして、てこ比の高い標準化されたピアソン残差は、推奨された境界の内側にあります。class2 を落とすことでモデルは改善されたようにです。
最大化コマンドと、とりわけ、ヘッセ行列によって標準誤差を自動で計算できたおかげで、従来の負の二項分布のモデル (NB2) は、苦労することなく最尤法によって構築することができました。
zero-truncated, zero-inflated, hurdle, censored models といった他の負の二項モデルも、ただ尤度関数を変更するだけで同様に構築できるでしょう。
この記事の改善にご協力くださった、編集者と審査員の提案と支援に感謝します。
M. L. Zwilling, "Negative Binomial Regression," The Mathematica Journal, 2013. doi:10.3888/tmj.15-6.