| 本アーティクルは The Mathematica Journal (volume 15, 2013) で発表されたもので、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 15, 2013) and the copyright holder is Wolfram Research, Inc." |
本アーティクルでは、耳障りなスクラッチ音を発生する数学モデルを紹介します。スクラッチ音は摩擦運動によって生じるもので、周波数スペクトルにカオス的特性があることからこうした音が発生します。ここで紹介するモデルは、ベースとなるロジスティックマップに摩擦振動のスティックスリップ特性が加えられています。その結果、黒板やガラス板を指で引っ掻いたときのような音を発生させることができます。
不快な音、例えば、黒板を指で引っ掻いたときに発生するような音の研究としては、最新の研究では心理音響学の観点 [1,2] から取り上げられたものがあります。我々は、このような音に関する研究を既に物理学的立場で行っていますが、本アーティクルでは、こうしたスクラッチ音を発生するための数学モデルを提示することにします。このような音は、摩擦系のスティックスリップ運動によって発生させることが可能で、そのメカニズムがロジスティックマップと緊密な関係にあることをここに示します。なお、ロジスティックマップでは、スリップ動作が周期的なものにしかならないため、弦楽器を弾くのと良く似たスティックスリップ的振る舞いとなるような特性を導入する必要があります。
周期的な衝撃力の影響下にある1次元の粒子運動については [3] に詳しく述べられています。以下に示すロジスティックマップは、この系における強い減衰の範囲 (strong-damping limit) から得られたものです。
ここで、パラメータ λ は 0 ≤ λ ≤ 1 にあり、xn の範囲を決定します。
ロジスティックマップは、カオス的振る舞いを説明する古典的な事例で、摩擦運動と深い関係にあることが知られています。ロジスティックマップによって式 (1) のパラメータ λ を 0.75 から 1 の間で変化させて発生する音は、[4] で検討されています。

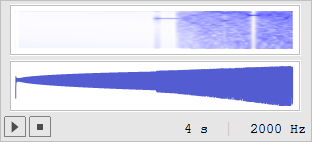
以下は、このプログラムを少し変更して、スクラッチ音と似た周波数スペクトルにしたものです。

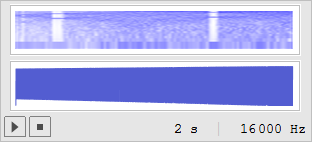
主な変更点は、サンプルレートを 16 kHz に上げたことです。カオス相を出入りするロジスティック系と耳障りでゾッとするような感じが一致するようです。
上記で説明したスクラッチモデルは、周期的なスリップモデルです。摩擦運動は一般にスティックスリップ現象として説明されます。バイオリンやその他の弦楽器を弾くことで生じる音は、多くの人が最も美しいとする音のひとつです。一方、黒板を指で引っ掻いて生じる音は、非常に不快なものと感じられるのがふつうです。しかし、音を発生するメカニズムは、どちらの場合も摩擦系のスティックスリップ現象で同じなのです。スティックスリップ現象は、スティック段階とスリップ段階の繰り返しからなります。図 3 は、弦を実際に弾いたスティックスリップ運動の音を示します。急激な立ち上がりの後に、一定の減衰が続く周期的な運動を認めることができます。前者はスリップ段階、すなわち、短時間の運動に対応します。後者はスティック段階、すなわち、弦が弓と共に一定の速度で動く部分に対応し、次のスリップになるまで続きます。
ロジスティックモデルにこのスティックスリップ特性をインポートするために以下の規則を導入します:
(a) もし、式 (1) で xn+1≥ xn であれば、すぐに変化が起きる。これがスリップ運動にあたります。
(b) もし、xn+1< xn であれば、(xn+1, xn) の x の値は、一定速度 Δx で線形的に減少する。これがスティック運動にあたり、Δx の値は弓の速度を決定します。
従って、以下に示すスティックスリップ現象をあらわす修正ロジスティックマップが得られます。
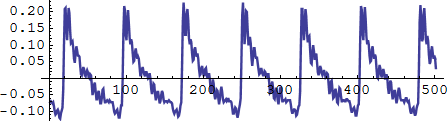
図4に示すのは、上記で説明した新しいロジスティックモデルのフローチャートです。左側の枝はスティック段階を、右側の枝はスリップ段階をあらわします。速度パラメータ Δx は、弦を弾く速度を与えるものです。
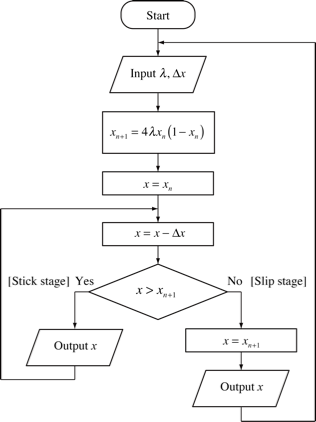
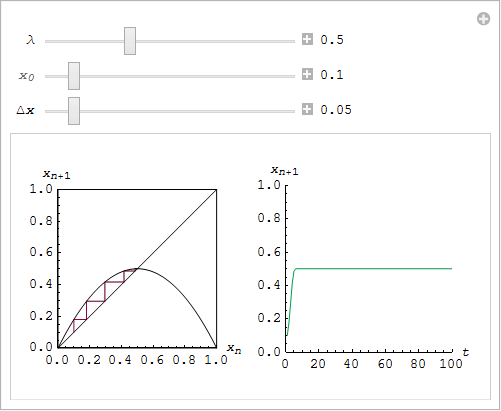
それでは、修正ロジスティックモデルの動きを見ることにしましょう。λ の値は、放物線の高さを与えるもので、0.5 と 1 の間で変化します。x0 は、x の初期値です。
まずはじめに、ロジスティック関数 f を定義します。

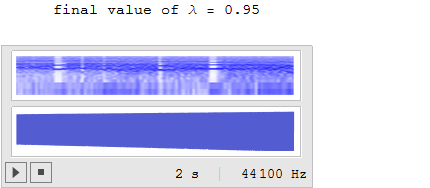
Linearly Modulated Model (線形変調モデル)
λ の値を 0.9 から 0.95 の間で直線的に変化させるものです。

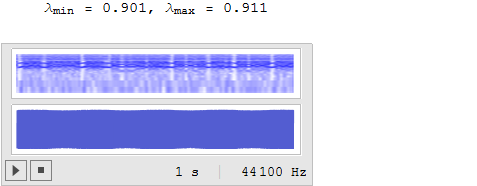
Sinusoidally Modulated Model (正弦波的変調モデル)
λ の値を、 0.901 と 0.911 の間で正弦波的に変化させるものです。

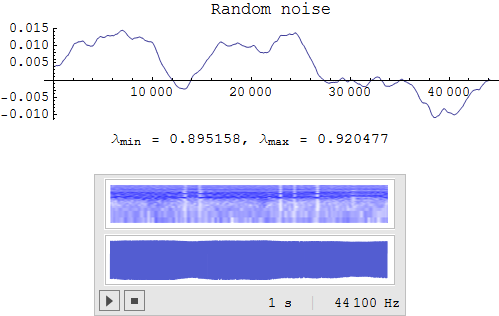
Randomly Modulated Model (ランダム変調モデル)
λ の値を、ローパスフィルタを通したランダムノイズで変化させるものです。

スクラッチ音は、強い不快感を引き起こすことが多いですが、この感覚を引き起こす原因が何であるかはいまだに解明されていません。本アーティクルでは、この問題の答えを求めるつもりはありませんが、その代わりに、このような不快な音を生成するモデルを提供します。上記で説明したとおり、スクラッチ音はカオスと深い関係がありますが、定常状態におけるカオスが必ずしも不快な印象となる原因となる訳ではありません。おそらく、カオス的領域を出たり入ったりすることがこの心理音響的な現象の主たる要因であると思われます。
セクション 2.2 の図2は、サンプルレート 16 kHz で λ 値を 0.9 から 0.95 の間で変化させたロジスティックマップにより生成される音が発生します。図9は、この分岐図とそれに対応するリャプノフ指数 (Lyapunov exponent) を示します [5]。リャプノフ指数が正であれば、系はカオスになります。負であれば、系は安定し、周期的に安定状態に収束します。安定状態はカオス領域の真ん中に突如としてに現れていることが分かります。

図 10 は、λ 値を 0.9 に設定した音を示します。定常ランダムノイズに似ており、ゾッとする印象は、図2の音に比べて少ないようです。この結果は、カオスそれ自体が不快感をもよおすのに必要な要因ではなく、カオスが出たり入ったりすることによってこの不快感が生じるのであろうことを示唆しています。

図 6 は、ここで提案したスティックスリップモデルによって生成した音です。λ 値は 0.9 から 0.95 の間で変動させ、サンプルレートは 44.1 kHz、追加パラメータ Δx は 0.08 に設定してあります。音響スペクトルは、図2の音と大きな違いはありませんが、このモデルはピッチ周波数を制御できます。事例 (図 6, 7, 8) は、様々な種類のパラメータ変調 (それぞれ、線形、正弦波、ランダム) を使って音を生成します。それぞれの変調範囲は、図9に示すように、少なくとも1つのリャプノフ溝が含まれるよう決定します。
ロジスティックマップに基づく数学的モデルを使って、黒板やガラス板を指で引っ掻いたときのような音を生成できることが分かりました。このモデルはカオス的な性質を示し、また、不快でゾッとする印象は、カオス的振る舞い、とりわけ、カオスを出入りする動きと深い関係があることが分かりました。こうして、摩擦運動のスティックスリップ特性を有する修正ロジスティックモデルが提示されました。しかし、こうした音の感じ方に対する心理音響的説明については今後の課題となります。
Y. Miki, "Using the Logistic Map to Generate Scratching Sounds," The Mathematica Journal, 2013. doi:10.3888/tmj.15-5.
ヤスシ・ミキ氏は、1970 年、1972年、1983年に東京大学で B.S.、M.S.、D.Eng. の資格をそれぞれ取得。研究の関心は、音響伝播と音響信号処理など。