| 本アーティクルは The Mathematica Journal (volume 14, 2012) で発表されたもの で、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 14, 2012) and the copyright holder is Wolfram Research, Inc." |
本アーティクルでは、ある多面体の頂点に菱形三十面体 (RT) を配置したときにできるクラスター (通常は面どうしをつなげる) について考察します。使用する多面体の辺の長さは、菱形三十面体 (RT) の原点から面までの距離の倍になるよう設定します (およそ 2.7527) 。こうしてできたクラスターを元に、菱形三十面体 (RT) や Wolfram|Alpha のロゴでもある菱形六十面体 (RH) を使って更にクラスターを構成できます。我々は、結合について他に種類がないかを簡単に調べ、RT の代わりに一致する多面体を使用して、元のクラスターから別のクラスターを作成します。
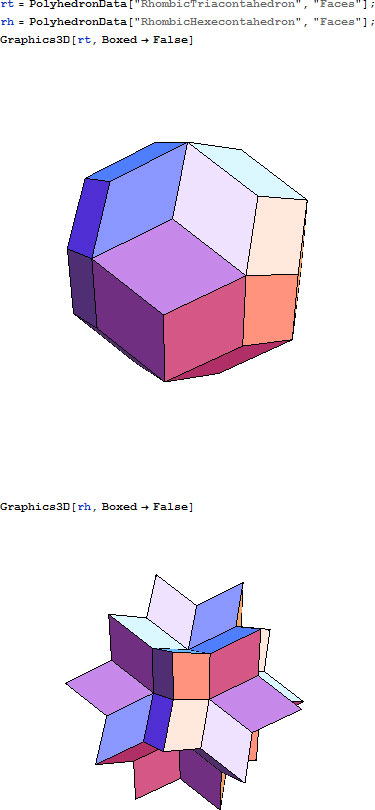
菱形三十面体 (RT) と 菱形六十面体 (RH) を、それぞれ以下に示します。
候補となる多面体を見つけるために、菱形三十面体 (RT) の原点から見たひとつの面の中心と各面の中心との相対的角度をそれぞれ以下にまとめます。
| face | radians | degree |
|---|---|---|
| 1 | 0 | 0° |
| 1 | π | 180° |
| 4 | π / 2 | 90° |
| 4 | π / 5 | 36° |
| 4 | 2π / 5 | 72° |
| 4 | 3π / 5 | 108° |
| 4 | 4π / 5 | 154° |
| 4 | π / 3 | 60° |
| 4 | 2π /3 | 120° |
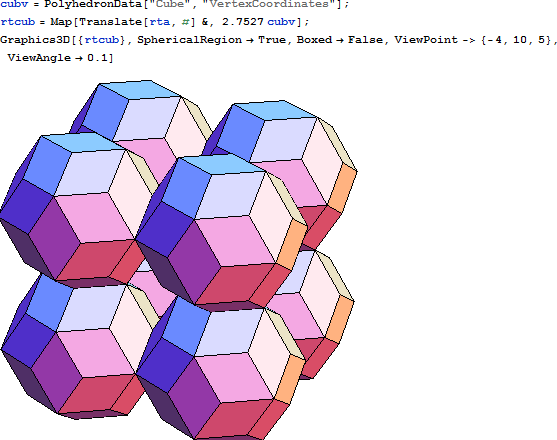
クラスターに適用できる寸法は、立方体と RT との関係から求まります。例えば、立方体の一辺の長さは、RT の面 (黄金比の菱形) の長い方の対角線と等しく、2 sin(arctan(1.618)) = 1.70129 となります。立方体の対角線の長さは、RT の三つの面で構成される頂点のうち対極にある2点間の距離と等しくなります。
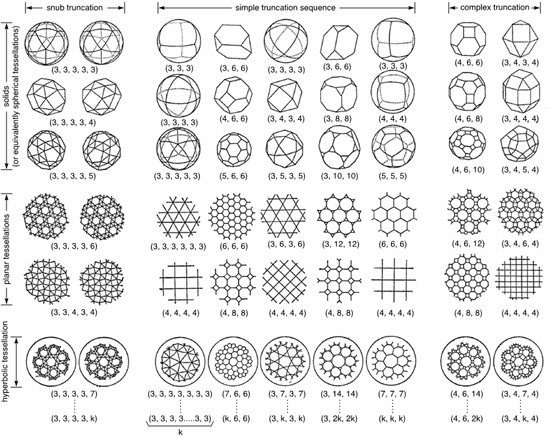
Szaniszló Bérczi が作成した切頂の表をみると、候補となる多面体を見つける別の情報が得られます。図1では、正多面体 (プラトンの立体) が球面に投射されています。これらの正多面体の頂点を切断したものがアルキメデスの立体になります。プラトンもしくはアルキメデスの立体は、その頂点の成り立ちで区別することができます。これらはどこを取っても一様だからです。頂点の成り立ちは、多面体の一つの頂点に集まる面を列記する Steiner 記号であらわします。例えば、(4,4,4) は、Steiner 記号で立方体をあらわします。立方体にはどの頂点にも正方形 (4つの辺からなる平面) が3つ集まっているからです。テーブルの3行目に従って RT 関連の構造を整理すると、(5,6,6), (3,5,3,5), (3,10,10), (5,5,5), (3,4,5,4), (4,6,10) となります。
 |
さらに、立方体に対する RT の関係、および、RH に対する RT の関係を検討するにあたり、必要となる全ての寸法を計算によって求めます。

立方体の辺の長さは、以下のとおりです。
立方体の対角線の長さは、RT の3つの面が集まる軸の対角線の長さと同じで、以下のとおりです。
RT の面の距離は、以下のとおりです。
RT の5つの面が集まる軸の対角線の長さは、以下のとおりです。
RT、立方体、および、黄金比の長方形の関係から寸法を求めることができます。

RT と RH、および、3つの面が集まる軸と垂直の関係にある平面 (RT と RH を二等分する平面) との関係を利用して、RT の各面どうしの角度を求めることができます。

構造に用いる定義は、以下のとおりです。

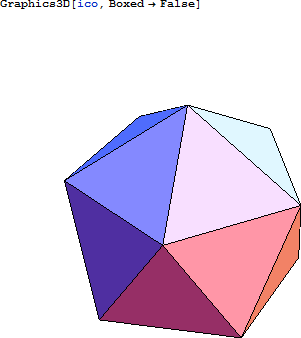
二十面体 (ICO) は、5つあるプラトンの立体のうちの1つです。
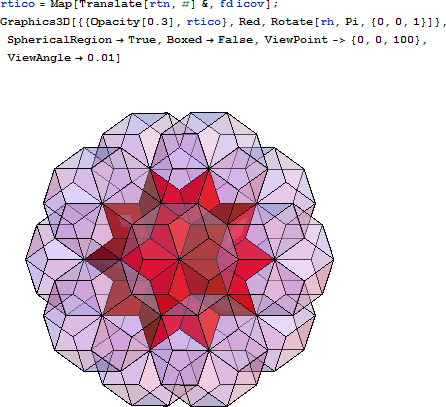
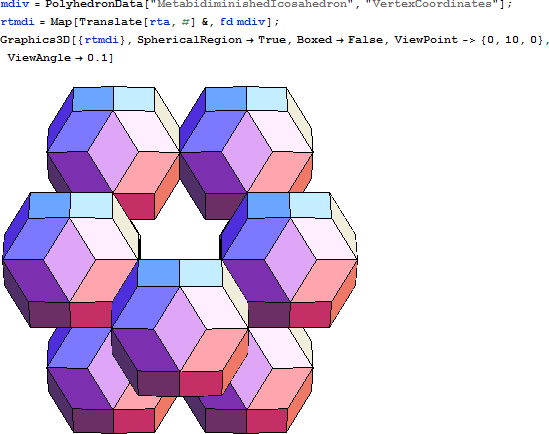
この二十面体の頂点に12 個の RT を配置するとその内部に RH ができます。準結晶の写真などでこの種の RT クラスターは見られます。
透過表示しない RH×12個のクラスターは、以下のようになります。
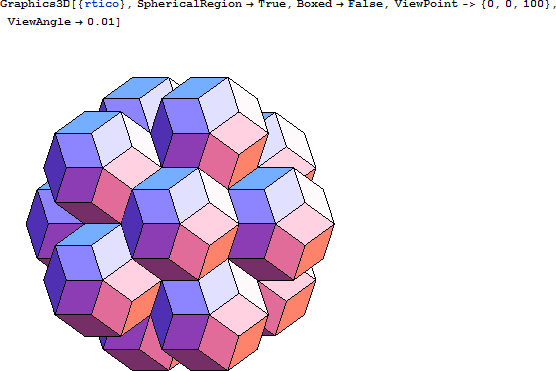
RT の代わりに十二面体を使用すると、十二面体の辺どうしがつながります。

切頂二十面体 (TICO) は、サッカーボールとしてもっとも広く用いられる形状です。この形状はまた、C60構造、つまり、バックミンスターフラーレンの全体構造でもあります。
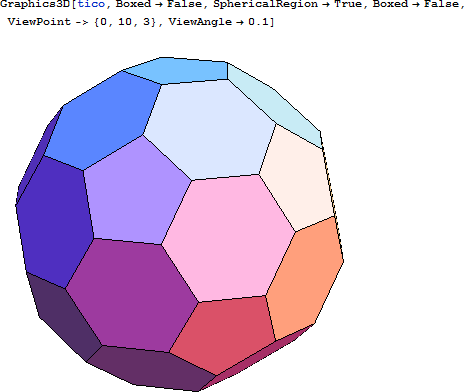

ここで、RT を切頂二十面体 (ICO) に置き換えると、ICO は辺と辺がつながります。

二十・十二面体 (ID) は、二十面体もしくは十二面体の頂点を切断してできる多面体です。
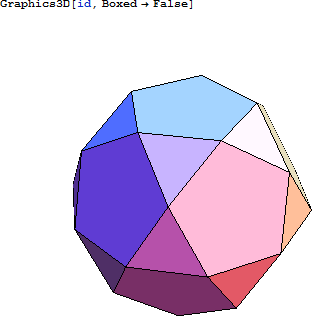
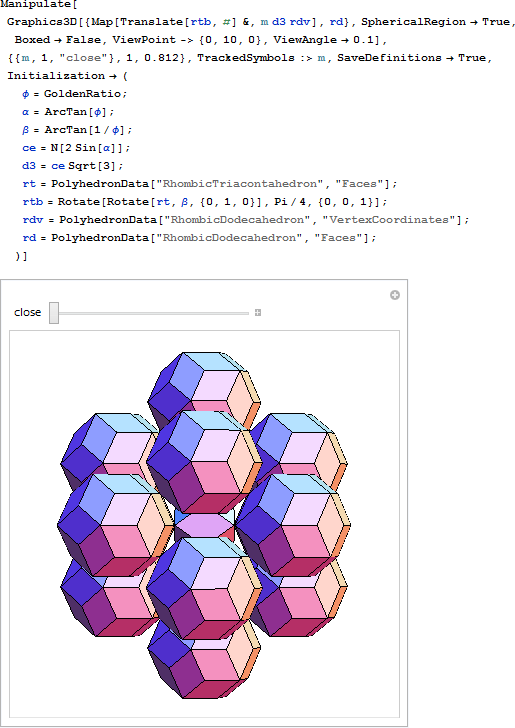
二十・十二面体 (ID) からできるクラスターは、以下のとおりです。

ICO の頂点に 12個の RT を 追加してみましょう。

続いて、十二面体 (DOD) の頂点に 12個の RH を追加します。

さらにいくつかの RT を ID の頂点に追加します。RT と RH をさらに追加することで、この構築を続けることができます。

十二面体の頂点を、辺の長さが一様になるように切断する特別なケースです。
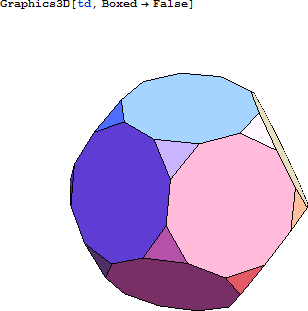
この 60個の RT からなるクラスターは、3個の RT が 20個組み合わせてできたものと解釈することができます。

一般的に見られる五角形の十二面体は、5つあるプラトンの立体のうちの1つです。
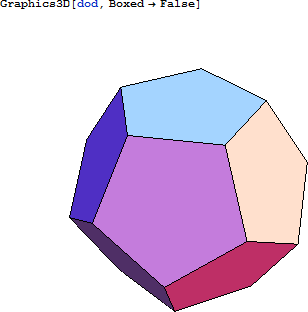
十二面体 (DOD) からできるクラスターは、以下のとおりです。

基礎となる多面体がそれに関連するクラスターとどのような関係にあるかを調べます。
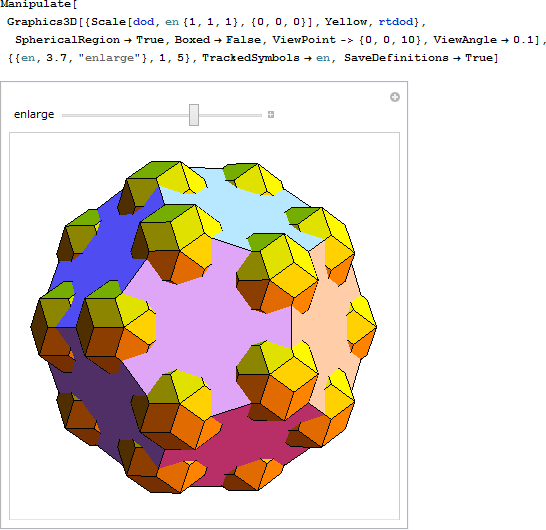
ICO の頂点に配置した 12 個の RH には、20個の RT のクラスターをあてまめることができます。

美しい形状です。準結晶の写真でこれと似たような形状を見かけることがあります。

大菱形二十・十二面体 (GRID) からできるクラスターは、以下のとおりです。
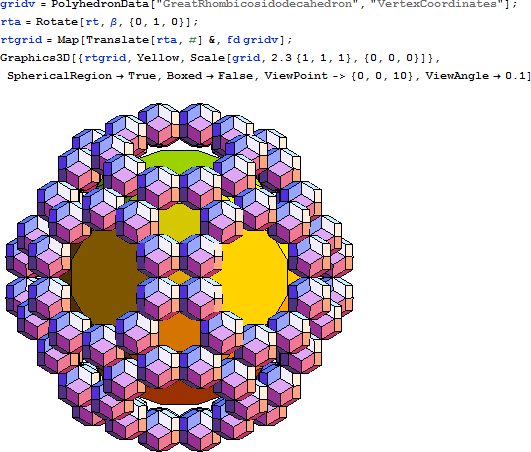
SRID には、60個の頂点があります。このクラスターでは、各 RT が隣接する 4つの RT とそれぞれつながります。TICO ベースのクラスターでは、隣接する RT が3つしかないのと対照的です。

小菱形二十・十二面体 (SRID) からできるクラスターは、以下のとおりです。

このクラスターに RH を加えて拡張することもできます。例えば ICO の頂点に RH を加えます。

様々な切頂体に対応するクラスターを以下にまとめます。
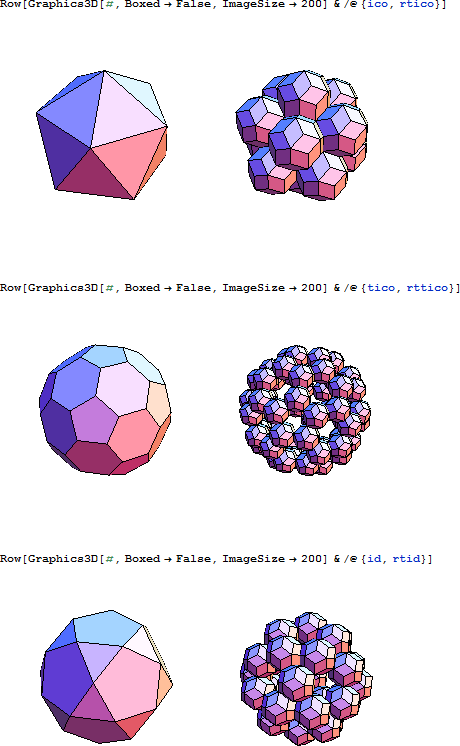
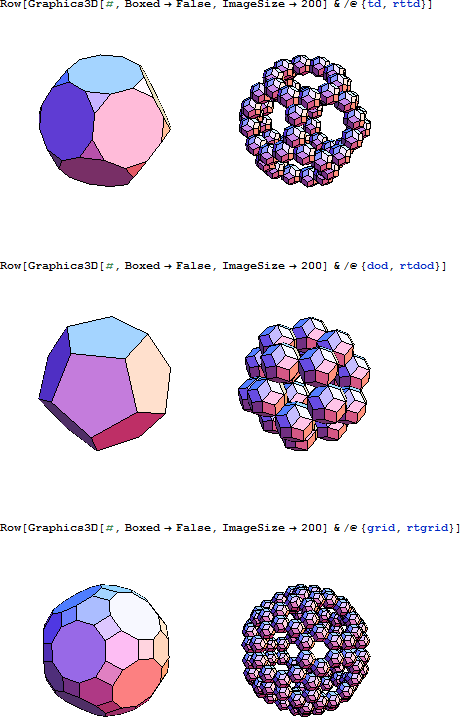
立方体は、5つあるプラトンの立体のうちの1つです。

立方体からできるクラスターは以下のとおりです。
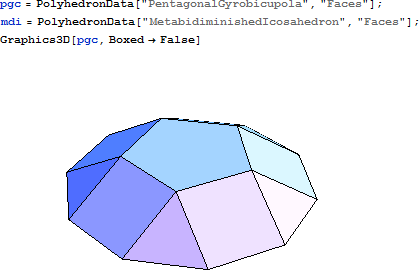
ジョンソンの立体の多くは、これまで紹介してきた多面体の一部である見なすことができます。このうち以下に示す2つを構造体として利用します。
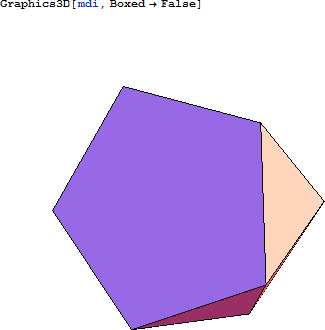
2つの立体からできるクラスターは、以下のとおりです。

Interesting clusters can also be produced when the RTs meet at their vertices. For instance, RTs at RT vertices meet with their fivefold tips.
RT の各頂点に RT を配置すると、興味深いクラスターができあがります。例えば、RT の各頂点に RT を配置すると、それらは5面の頂点と一致します。

RTs at the vertices of a rhombic dodecahedron (RD) meet with their threefold tips. Adjacent pairs of RTs overlap in a flat golden rhombohedron, creating another closed structure.
菱形十二面体 (RD) の各頂点に RT を配置すると、それらは3面の頂点と一致します。隣接する RT のペアは、平面黄金菱形十六面体と重なり、閉じた別の構造体ができあがります。
S. Kabai, Sz. Bérczi, and L. Szilassi, “Some Clusters Produced by Placing Rhombic Triacontahedra at the Vertices of Polyhedra,” The Mathematica Journal, 2012. dx.doi.org/doi:10.3888/tmj.14-14.
Sándor Kabai は、1970年にハンガリーの Bánki College で生産技術における B.Sc. を取得した退職技術者です。彼は、Wolfram Demonstrations Project において、多くのデモンストレーションを作成してきました (demonstrations をご覧ください) 。彼は、ハンガリーで空間研究に関する教育のコンサルティングを行っています。
Szaniszló Bérczi は、1974年に Eötvös Loránd University で物理学と天文学の M.Sc. と、1994年には Hungarian Academy of Science で地質学 (惑星科学) の Ph.D. を取得しました。彼にはいくつかの分野における実績があります。彼は、the material hierarchy versus great structure building periods に従って物質の進化の新しい合成を作りました。このモデルは、Eötvös Loránd University における彼のレクチャーノート・シリーズの一部です。彼はまた、Geonomy Scientific Committee of the Hungarian Academy of Science 内に、物質の進化における研究グループを (Béla Lukács と共に) 編成しました。彼は、惑星科学におけるハンガリーでの最初の本、From Crystals to Planetary Bodies (ハンガリー語) を執筆しました。Eötvös Loránd Universityで、彼は (同僚と共に) Hungarian University Surveyor (Hunveyor) 実験的宇宙探査モデルと教員をトレーニングするための Husar rover (Hungarian University Surface Analysis Rover) の立ち上げと設立を行い、新しい計測技術を開発しました。彼は対称性と構造構築における最初のレクチャーノートブックをハンガリー語で執筆し、そこではセルラーオートマタモデル形成において対称原理を用いています。彼は、ヒューストンにあるJSCからアメリカ航空宇宙局 (NASA) の月のサンプルと、国立極地研究所 (NIPR) から南極隕石ラボラトリの南極隕石を、Eötvös Loránd University が借りられるよう手配しました。そして、惑星物質の研究と、工業原料と技術の比較を開始しました。古代ユーラシア美術の彼のブックレットシリーズは、広大なユーラシア地域の形象美術・装飾芸術の両方を調査しています。彼の民族数学の研究は、古代ユーラシア文化を網羅しています。
Lajos Szilassi は、1966年にハンガリーの University of Szeged で空間幾何学の M.Sc. を、2006にはPh.Dを取得しました。彼は、現在 University of Szeged の名誉教授です。彼の主な教育分野には、幾何学、初等数学、コンピューター利用技術が含まれます。彼の研究分野は、可視化ソリューションを備えた、数学・幾何学問題のコンピューターによる解法です。1977年に彼はトロイダル7面体を構成する方法を発見しました。これは、シラッシの多面体として知られています。