| 本アーティクルは The Mathematica Journal (volume 14, 2012) で発表されたもの で、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 14, 2012) and the copyright holder is Wolfram Research, Inc." |
宇宙船を月面に着陸させる問題を考えるとき、空力と月以外の物体の重力は無視できるほどわずかであり、横移動は無視できると仮定することができます。その結果、降下軌道は垂直となり、推力ベクトルは軌道の接線となります。
宇宙船が月面の近くにいるため、月面の重力加速度を一定値 g = 1.63、排出ガスの宇宙船に対する相対速度が一定、その質量変化率 m‘(t) は –μ ≤ m‘(t) ≤ 0 によって制約されていると仮定します。ここで、μ は燃料の燃焼による質量の最大の変化率とします。
問題は、最小限の燃料で月面に軟着陸することです。
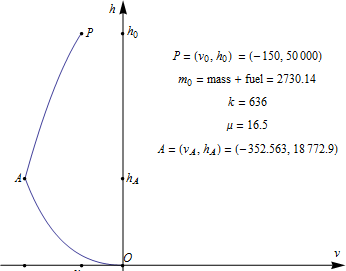
これは着陸直前のシステムのイメージです。
参考文献 [1, pp. 247–248] と [2] に従って、ここでは下記の表記と仮定を使用します。
ここでもう一度、我々の仮説を引用すると、月以外の物体の空力と重力は無視してできるほどわずかであり、横方向の動きは無視されるため、降下軌道は垂直方向で、推力ベクトルは地面に対して垂直になります。
我々はまた m0= m(0) = M + F と仮定しています。M は燃料を除いた宇宙船の質量、F は燃料の初期質量です。宇宙船が地球に戻ることを想定すると、離陸用の燃料が必要となるため、m(t) > M となります。
ニュートンの第2法則により (参考文献 [3] と [2]) 、
連立方程式で表すと
k は定数です。3つ目の方程式では 1秒あたりの質量の減少量 (1秒あたりの噴出で燃焼する燃料) が噴出の推力に比例していることを示しています。
我々の目的は、燃料の消費を最小限に抑えることですので、コスト汎関数は次式になります。
ここで b は、次式を満たす開始時点です。
したがって、計画対象期間 (horizon) は [0, b] となり、この b を求めることになります。
ベクトル形式で x(t) =(x1(t), x2(t), x3(t)) = (h(t), v(t), m(t)) ならば、
となり、問題を
のように書くことができ、最終的に、
のようにできます。方程式 (3) から
を導くことができ、区間 [0, t] の積分によって
を得ることができます。以下の場合にのみ、h‘(b) = 0 となります
m (b) の値を解くと、
となり、これを方程式 (5) に代入すると
となります。この結果は、参考文献 [2] で発表されています。
方程式 (5) を(6) 及び (7) の条件で考えてみます。任意の h(0)、h‘(0) 、g および k に対し、宇宙船を停止させるのに必要な燃料量、すなわち h(b) = v(b) = 0 を満たす燃料量は、終端時間 b の狭義単調増加関数です。
(6) と (7) の条件で、 (5) の終端時間 を最小にすることは、燃料消費量を最小にすることと同じです。
ここから (7) の代わりに次のコスト関数を考えることができます。
したがって、条件 (7) における式 (6) は、条件 (8) における式 (6) として考えることができます。これは Mayer 型の最適制御問題です (参考文献 [4] 第4章参照)。
議論が長くなるのを避けるため、私たちは参考文献 [4] の定理 4.2.i の短いバージョンを利用します。Mayer 型問題は次のように表されています。
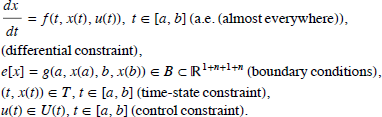
(x(t), u(t)) の対 (a ≤ t ≤ b) は、x:[a, b] → 
n が絶対連続であり、u:[a, b] → m が測定可能であり、x と u は方程式 (10) を満たす場合、admissible (許容可能) または feasible (実行可能) となります[参考文献 5]。Ω を admissible pair (x, u) クラスにしてみましょう。目標は、Ω に対するコスト関数 Λ (x, u) の最小値を見つけること、すなわち、すべての (x, u) ∈ Ω に対する -∞ < Λ (x*, u*) となる要素 (x*, u*) ∈ Ω を見つけることです。我々は乗数 (multipliers) と呼ばれる変数 p = (p1, …, pn)、およびハミルトニアン (Hamiltonian) と呼ばれる、以下によって T × U × n で定義される補助関数 H (t, x, u, p) を導入します。
ここで
と定義します。必要な仮定を追加します：
1+n において閉じている。1+m+n において閉じている。)
これら 8つの仮定を前提として、(x* u*) を Mayer 型問題 (9) と (10) の最適対にします。最適対 (x*, u*) には必ず次のような属性があります。
(a) 次のような絶対連続関数 p(t) = (p1, …, pn)があります。
d g が e [x*] で完全に 0 でない場合、p(t) は [a, b] でゼロになりません。
(b)ほぼすべての固定の t ∈ [a, b] (a.e.) で、 ハミルトニアン (u にのみ依存する関数) は最適戦略 u*=u*(t) で U の最小値を取ります。すなわち、M[t, x(t), p(t)] = H[t, x(t), u*(t), p(t)], t ∈ [a, b] (a.e.) となります。
(c) 関数 M(t) = M (t, x(t), p(t)) は [a, b] のほとんどすべてのところで絶対連続関数と一致します。
となり、p1 = c1、p2 = –c1t + c2、0 ≤ t ≤ b となります。c1 と c2 は定数です。
–p2k x3-1 + p3 > 0 の場合、H の最小値は u =0 で達成され、
となります。これは、宇宙船の自由落下に相当します。
–p2k x3-1 + p3 > 0 の場合、最小の H は u = –μ で達成され、
となります。これにより、制御関数 u は極値 0 および μ のみ取ることが判ります。
区間 [τ1, τ2] に u = 0 がある場合は、
となり、t ∈ [τ1, τ2] の場合は、
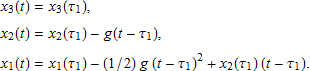
となります。この場合、(x1, x2) は放物線の弧を描きます。
区間 [τ1, τ2] に u = –μ がある場合は、
となり、t ∈ [τ1, τ2] の場合は、
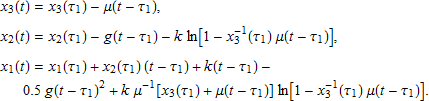
となります。
軟着陸に対する数学的アプローチにおける前提条件がすべて満たされている場合、τ はエンジンの点火時間、b は着陸時間で、x1(b) = x2(b) = 0 となります。b と τ1 に対する以下の連立方程式
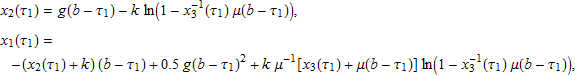
が解を持つ場合、 (6) および (8) により与えられる最適制御問題の解となる最適対 (x*, u*) が存在します。
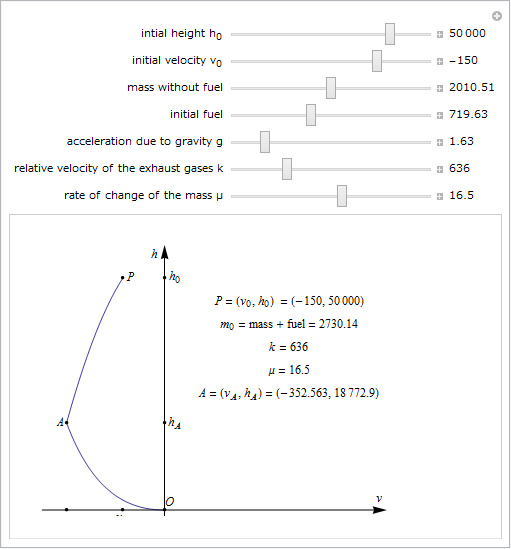
MoonLanding は、月面軟着陸のための Mathematica プログラムです。h0 は初期高度、v0 は初期速度、mass は燃料のない状態の着陸船の質量、fuel は初期燃料、g は重力加速度、k は排気ガスの相対速度、μ は燃焼による質量の変化率です。
結果の正確性は、プログラムの非線形方程式系を解くのに使用する変数 z と g の初期値によって大きく異なってきます。
次の Manipulate によってパラメータをリアルタイムに変化させることができます。
Babes-Bolyai 大学 (ルーマニア、クルジュ＝ナポカ) 数学・コンピュータサイエンス学部の Horia F. Pop 氏へ、貴重な議論に対し、感謝の意を表します。
Marian Mureşan, “Soft Landing on the Moon with Mathematica,” The Mathematica Journal, 2012. dx.doi.org/doi:10.3888/tmj.14-13.
Marian Mureşan、Babes-Bolyai 大学 (ルーマニア、クルジュ＝ナポカ) 数学・コンピュータサイエンス学部に所属。解析、非線形解析、変分法、および最適制御に関心を持つ。