| 本アーティクルは The Mathematica Journal (volume 14, 2012) で発表されたもの で、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 14, 2012) and the copyright holder is Wolfram Research, Inc." |
本アーティクルでは、拡散過程を NDSolve を使ってモデル化する方法を述べ、それを、プロシージャ型、関数型、ルール・ベース型、モジュール型のプログラミング法を使った読者が独自に開発した手法と比較します。拡散方程式に基づいていますが、他の偏微分方程式にも応用できます。
Mathematica の組み込み関数 NDSolve を使い、偏微分方程式を解く事は大変簡単ですが、実際の行なわれている事が隠されてしまう事もあります。微分方程式に Mathematica を使う事に関しては、いつでも参考文献を参照できます [1, 2] 。様々なプログラミング手法を試す事によって、読者自身の手法を NDSolve に組み込む事も可能です [1] 。本論では、沢山の資料があると言う事実と、それ自身が大変に興味深いという事実を鑑みて、拡散方程式を対象とします [3, 4, 5] 。なお、本論では Mathematica 8 が使われています。
拡散過程のモデル化 (注:伝統的には「数学的定式化」、すなわち、現象を方程式として表現する事)、すなわち、拡散方程式から始めましょう。まず、連続の方程式は以下の様になります:
ここで ρ は密度、t は時間、ui は速度場の第 i 成分です。拡散係数 D が定数と仮定すると拡散方程式は以下の様に書けます:
完全に一般化すると以下の様に書けます:
ただし、Dij は、拡散係数を要素とする正値行列で、各行列要素 (すなわち、個々の拡散係数) は、位置と時間に依存してもしなくてもかまいません。行列は、拡散テンソルと呼ばれています。
まず、組み込み関数が所与の問題をただちに解けるかどうか試してみます。手順としては、まず、DSolve を使い、それが偏微分方程式を解けそうにも無い場合は、NDSolve を試してみます。ここでは、(空間次元については) リング (輪) について解くとします。すなわち、空間次元は一次元で済みます。この場合、拡散方程式は以下の様に書けます:
ここで、DSolve を試してみます。
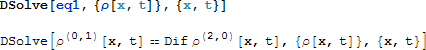
DSolve は、余りに素朴に定式された問題の解に達する事はできません。次に、初期条件を設定してみます:
上記の初期条件を組み込んで、再度試してみます:
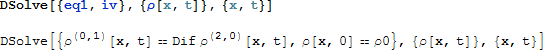
またもや失敗しました。首尾よく結果を得られるまで、初期条件をいろいろと 試す事も出来るかもしれませんが、NDSolve を試してみることにします。ここで、ガス・チューブの中の拡散過程を調べようとしているとします。議論を簡単にするためにチューブは一次元であるとします。すなわち、固定長 1 のリングであるとします。さらに、このリングを「解いて (ほどいて) 」線にして、この線上で解を表示します。(発展方程式として、時間方向には) 10 単位時間について方程式を解いてみます。また、拡散率を以下の様に設定します:
初期密度の値を 0 に設定します:
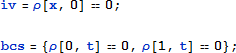
全ての要素を NDSolve の中に取り込めば、補間関数の形式で解を得ることができます:
上記の解関数を表示してみましょう:
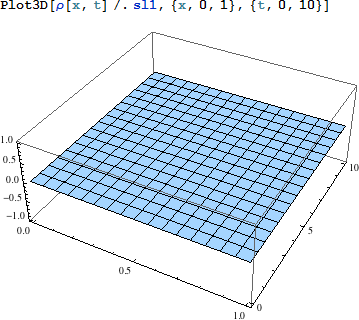 |
他の初期条件、例えば、正弦波的であるとします:
解を求めてみましょう:
上記の解を (時間方向一次元、空間方向一次元で) 表示してみます。
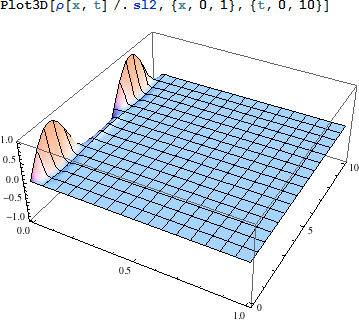 |
これは、密度が直ぐに 0 に落ちてしまうので、あまり現実的には見えません。D の値を決める必要があります。たとえば 1 にしてみます:

上記の解を表示してみます:
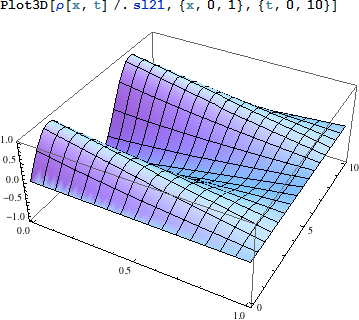 |
これは、図 2. よりは現実的に見えますが、境界条件が合っていません。もし、これを円と考える (空間次元方向を丸めてリングにする) と、(x = 0 から x = 1 に向かって進み最後に) x = 1 から x = 0 に戻った (元々リングなので x = 1 と x = 0 は同一地点である) 途端、不連続が出現します。周期境界条件を使い、リング解を修正する必要があります:
(空間的な) 一様密度 1 をいう条件を課していますが、原点の密度が 0 になる場合もある時間的に正弦波的な境界条件なので、境界条件が合いません。境界条件と初期条件が矛盾するという警告が表示されますが、何とか解は得られます:
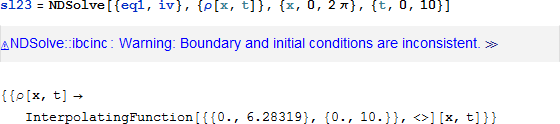
上記の解を表示してみます:
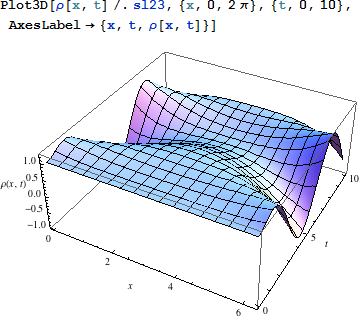 |
上記の表示は道理に合っている様に見えます。境界条件は、今や、リングに沿って周期的です。これを実現するためには、どのようなプログラムを書けばよいでしょうか?
FORTLAN や C++ や Java のような言語でプログラミングをした経験のある人は、プロシージャ型プログラミングという概念にも慣れているでしょう。プロシージャは、ループ構造 (繰り返し構造) の中で実行されます。所与の問題を解くために、有限差分のスキームを実装してみます。
まず、拡散方程式を同等な有限差分に変換します:
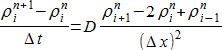
ここで、リングは、X 個のセルに、時間は N ステップに分けられているとします。所与のセルの密度を、第 i th セルが第 n th 時間ステップで特定します。すなわち、i は、0 から X まで、時間は 0 から N まで走ります。任意の時間ステップにおいて、次式が成り立ちます:
安定性の条件 [2] は、以下に様になります:
もし、この係数 (上記の不等式の左辺) が 1/2 より大きい場合は、解の時間発展は不安定になります。以下の様に書きなおしてみます:
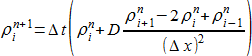
ρ の初期条件にある値 ρ0 が与えられているとすると、次の時間ステップでの ρ の値を得るために、上記の式を使う事ができます。これらの値を新しい ρ0 の値に取り直して (時間ステップを進める) 計算を続けます。初期条件を確定し、プロシージャ型の繰り返し操作 Table[function,{iterator}] を使って、この結果を作り出してみます:
位置は 0 から 6 までとする:
現在の時刻を初期条件とするように時間を進めます。問題のリストの部分は、list[[indices of sublist]] を使って特定します:
周期的境界条件は次の通りである:
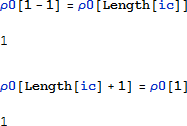
これで、初期条件が確立され、最初のステップが完成しました。
次に、時間を一ステップ進める関数を構築するため、まず、If[condition,condition is met,condition is not met] を使い、境界条件を含むように ρ [x] に書き換えます:
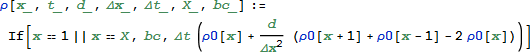
これをテストしてみます:

再度 Table を使ってリストを生成し、時間ステップ一つ進める関数を作ります:
正しいかどうかチェックします:
Table を使い、時間発展する解を構築します:
これで、モデル開発を終了しました。
結果を表示してみます。以下のように、run1 というテストを実行します:

テストの結果を表示します:
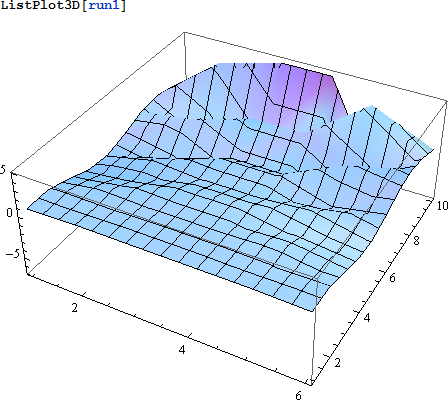 |
上記の解は、非常に速く、滑らかさが消えて乱雑になってしまいます。実は、D の値をが安定性の条件を壊す様に選んでしまったのです。別の値で試してみます。(3) 式より、 D ≤ 1/4 だとよいようです。ρ0 を再初期化する必要があります:

D に対する正しい値を使って run を記述します。
正しい D の値を使って、run を構築します (文字が同じで紛らわしいが、run 関数を実行した結果を前回と区別して run2 としてみる) :

このテスト結果を表示すると次のようになります:
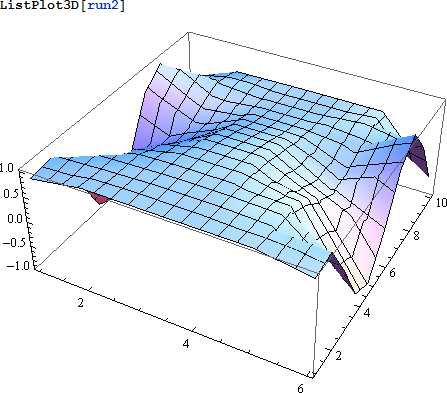 |
前のよりは良く見えます。これは、多少のノイズはあるものの、NDSolve で得た結果と同様に見えます。より厳密で正確な解を求めるのであれば、より微細なグリッドとよりよい差分スキームを使わなければなりません。しかしながら、それは別の論文に任せるとしましょう。
x に f を作用させた f (x) を使うプログラミング・スタイルもあります。
Function[body][parameter replacement] を使って、伝統的な方法で関数を構築する事から始めます。ここで記号 # は、形式的な引数を表します:
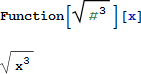
上記の定義式は、Function という命令後を使わずに短形式で書く事も可能です。ただし、定義式が完了した事を Mathematica が知るために、定義式の最後に & を付記する必要があります:
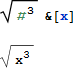
引数が 2つあるときは、#1 と #2 を使います:
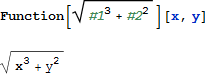
これも、短形式で書く事ができます:
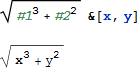
Map[function,list] コマンドを使い、リストの各要素に関数を作用させることができます:
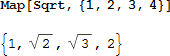
上式は、function/@ という短形式を使う事もできます:
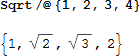
これは、以下と同等です:
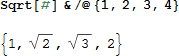
関数型プログラミングを使って、拡散方程式をプログラムします。まず、リングの中のセルからなるリストを定義します。
Range[max element] を使い、(要素が) 1 から max element までのリストを作ります:
ここでは、1 から 6 までにしよう:
初期条件を定義します:
初期条件として、あらゆる場所で 1 であるような場合を選択しよう。すなわち、各位置において、自分自身 (位置の座標の事) で割る関数を設定すれば良い:
次に、拡散方程式を定義します。周期境界条件とリストを使っているので、左右に回転 (ローテーション) するだけです:
上式をテストしましょう。まず、前章の ρ のプロシージャ型の定義をクリアします:
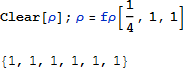
境界条件を制限する必要があります。ReplacePart[list,{parts and replacements}] を使い、両端の要素を境界条件で置き換えます:
これらをテストしてみます:
時間方向の 1 ステップを構築します:
上式を試してみます:

最終結果を生成するための表を構築します:
これを試してみよう:

この結果を表示します:
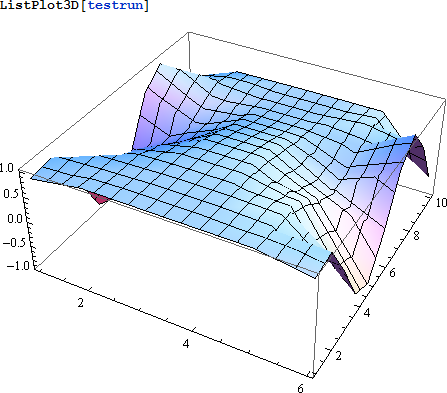 |
プロシージャ型プログラミングと同じ結果を得られました。
表現を変換するという Mathematica の数式処理的な性質を使ったプログラミングも可能です。ルール・ベース・プログラミングは、表現をそれら形式に基づいて書きなおす変換ルールの概念を使います。![]() という表現を例にとり、変換ルールを作用させてみましょう:
という表現を例にとり、変換ルールを作用させてみましょう:
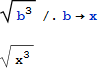
以下は、より複雑な例です:
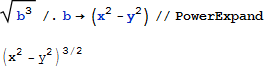
拡散方程式に適用するため、初期条件から始めます:
実行してみます:
次に拡散方程式を定義します。ここで、ρ0 の後のダブルのアンダースコア __ は、(ρ0 が) リストであることを表しています:

例えば t1 を定義します:
境界条件を定義します:
最初の時間ステップについて試してみましょう:
上式を更に試してみましょう:

FoldList コマンドを使ったモデルの値を特定するため、中間的な関数を含める必要があります:
runt1 というモデルを生成します:

結果を表示します:
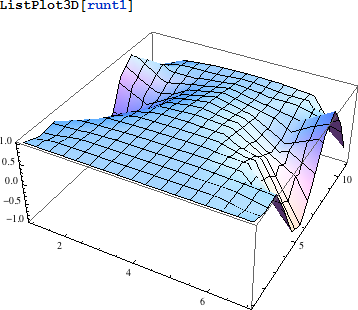 |
スコープ構文は、シンボルの有効範囲を局所的にします。局所化されたシンボルは、グローバルな値を生成したり再定義したりしません。局所的なオブジェクトの名前は、Module[{names},expression] を使って作り出す事ができます。Block[{variables},expression]を使って、変数に値を一時的に割り当てる事もできます。ここでは、Module コマンドを使う事にします。
今までやった事をモジュールで構成します:

上記の関数を実行した結果を表示します:
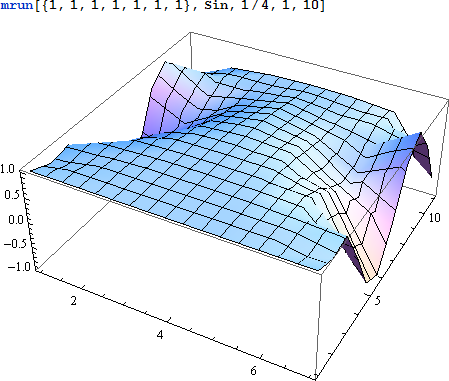 |
Mathematica の標準的なプログラミング・パラダイムが、拡散問題に適用出来る事を見て来ました。本論は、拡散問題の表面を引っ掻いたに過ぎません。本論で紹介した様々な手法は、NDSolve に対する新しい手法のテンプレートにすることができます。それらの実装は [1] で述べられています。新しい手法を Mathematica の関数の既存の構造の中に導入出来ると、この柔軟性は非常に強力です。もちろん、もっとも強力なプログラミング手法は、様々なパラダイムを融合します。
G. E. Hrabovsky, “Diffusion Modeling,” The Mathematica Journal, 2012. dx.doi.org/doi:10.3888/tmj.14-6.
ジョージ・ヘラボフスキーは、非営利の科学調査および教育組織である、マディソンエリア・サイエンス&テクノロジーの社長であり創設者です。彼は20年以上に渡る Mathematica ユーザでプログラマです。彼は、理論物理学や天文学、計算物理を研究しています。