| 本アーティクルは The Mathematica Journal (volume 14, 2012) で発表されたもの で、著作権は Wolfram Research, Inc. に属します。 |
| "This article was previously published in The Mathematica Journal (volume 14, 2012) and the copyright holder is Wolfram Research, Inc." |
我々はまず、木星の重力によって混乱する小惑星運動の平面上のケプラー問題を解いてみます。軌道要素それぞれの微分方程式の結果を解析することで、2:1 共鳴 (木星の 1回の公転に対して、二回公転する小惑星) においてギャップ (空隙) が生まれるメカニズムを明らかにし、さらに他の共鳴 (3:2、3:1 など) の場合について簡単に言及します。また、これらの共鳴において運動が無秩序になる理由についても論じます。
本稿の目的は、方程式
を解くことです。μ は太陽の質量と重力定数の積、r は小惑星の 2次元空間の位置 (ベクターを複素量として表すので、r は対応する長さとなります) 、そして ϵ f は木星の摂動力を表し、最もシンプルな形式では
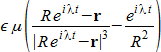
と等しくなります。ここで ϵ ≃ 0.001 は (太陽の質量に対する相対的な) 木星の質量、R eiλt は (太陽の中心に対する相対的な) 木星の位置となります。ここでは、木星の軌道が小惑星の軌道面で半径 R の完全な円を描き、λ はその一定の角速度であるとします ([1] を参照) 。
(1) を解くために、
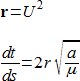
として、新しい従属変数 U と新しい独立変数 s を導入します。a は s の正の (かつ、現時点では任意の) 関数です。この定義は r = ![]() (は U の複素共役を表します) を意味します。
(は U の複素共役を表します) を意味します。
そこで、元の方程式は
(プライム ‘ は s に関する微分を示しています) を読み込みます。
これを次のように検証します。
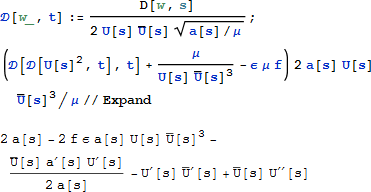
f = 0 の場合、(4) の一般解が
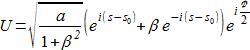
であることは容易にわかります。a、β、s0、ϕ はここで、軌道要素 (orbital elements) と呼ばれる任意定数 (a > 0 かつ 0 ≤ β < 1 を条件とする) です。続いて、この解が方程式 (4) (ここでは a‘ = 0 かつ f = 0 なので、簡約化されます) を満たしているか検証します。

U を2乗すると
となり、これは初めに x 軸に沿って引き伸ばし、次に角度 ϕ で回転した一般的な楕円 (a は楕円の長半径の長さ、はその離心率) です。残りの軌道要素 s0 は遠日点における s の値です。
f が 0 以外の場合、軌道要素を s の緩変動関数とし、U そのものを
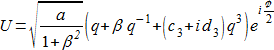
へ展開できるようにする必要があります (ここで c3 + i d3 は小さな値の複素数となり、また q ≡ ei(s–s0) とします) 。一般的には、大括弧で q の奇数乗の項 (負のものも含め) をすべて囲むべきですが、我々の目的にはこの形式で十分です。
試行解である (7) を (4) の左辺に代入して、ϵ と β の 2次以上の項は十分に小さいため切り捨て、q について整理すると q-2、q0、q2 の以下の係数を得ます。

方程式の右辺を同様に展開して得られる q-2、q0、q2 の係数と一致する必要があります。
これからその作業を行っていきます。
この後の計算を簡約化するために、μ と a (木星に対してちょうど 2:1 共鳴の場合 ※[2] を参照) の両方が 1 と等しくなる単位を用います。こうすることで、摂動力 (2) では R = 22⁄3 かつ λ = 1⁄2 となるので、新しい時間の単位は大体1年 (正確には 0.944 年) となります。(3) の 2行目から、高精度で (すなわち、非摂動解を用い、高次の β の項を切捨てて)
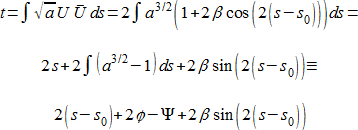
を得ます。
s の原点を適切に選択することで、通常追加される積分定数を常に除去することができます。
最後の等式は ”resonance (共鳴) ” と呼ばれる変数
を定義します。
a ≃ 1 であるので、
とすることができます。
t を (8) の最後の行で置き換えると、木星の位置は以下のようになります (R = 22⁄3) 。
これで (4) の右辺を展開して q-2、q0、q2 の係数を評価する準備が整いました。

(4) の左辺と右辺で q-2、q0、q2 の係数を比較することで、a‘、β‘、ϕ‘、s0‘、c3、d3 についての 3つの複素数 (6つの実数の) 一次方程式が生じます。これらは簡単に解くことができ、結果として a‘、β‘、Ψ‘ それぞれについての以下の 3つ式をもたらします。

いずれの場合も、対応する β-展開式の最高次のみが保持されます。その他の項は、結果の解にわずかに影響しているに過ぎないことがわかります。
2:1 共鳴、もしくはそれに近い場合の小惑星の軌道要素を強制的に変更することは、次の3つの微分方程式によって十分な精度で表されます。
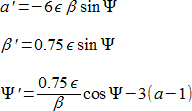
明らかに a‘ + 8 β β‘ =0 が成り立つので、a + 4 β2 ≡ 1 + K が運動の定数であることを意味しています。(12) の最後の式に β を掛け、a を 1 + K – 4 β2 で置き換え、右辺の全ての項をまとめると
となります。それぞれの項に β‘ を掛ける (もしくは、0.75 ϵ sin Ψ を掛ける) と
という結果になります。これにより
が他の運動の定数であるということがはっきりとわかります。K = 0.016 の場合の等高線は、(12) の解には 4つの異なった型があることを示しています。
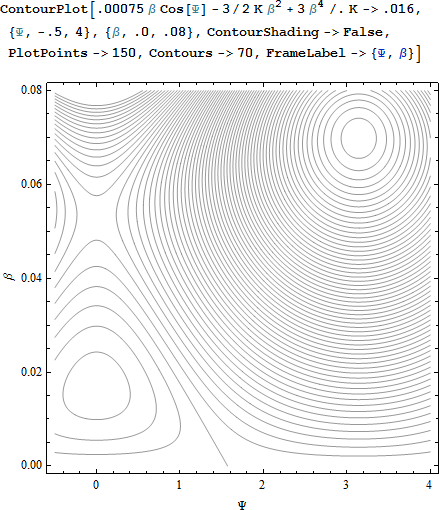
可変共鳴の振動を伴う 2つの中心 (Ψ = 0 で離心率の小さな中心と、Ψ = π で離心率の大きな中心) と、その領域があることがはっきりわかります。この 2つの領域の間に、離心率が大きなところで Ψ が円運動する (双曲線の固定点によって分けられている) 2つの領域があります。
4つの全て状況で β とそれに対する a は規則的に振動するので、ここには共鳴領域を一掃する動きはありません。これを満たすには、さらなる摂動が必要です。
その話に入る前に、別の重要な事実を述べる必要があります。それは、前述した 4つの領域の解は K > 0.0119 である時にだけ生じるということです。K がこの ”臨界値” に達するや否や、以下のプロットに示されるように領域 Ψ = π で離心率の大きな解のみを残して、Ψ = 0 の中心と と双曲線の固定点が一つに融合し、やがて (K < 0.0119 の場合には) 両方とも消滅します。
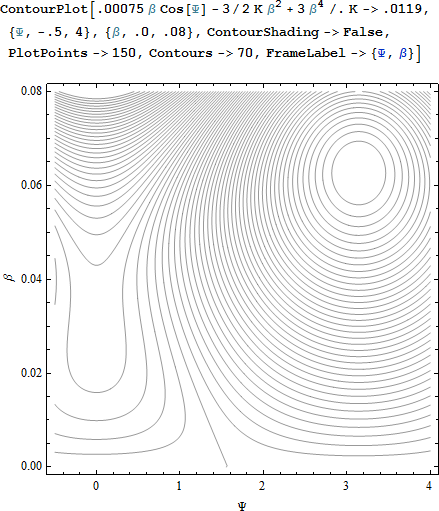
これは次で述べる、間隙を一掃する実際のメカニズムの理解に役立ちます。
軌道上の全ての天体は、定期的に天体の破片 (流星体など) と衝突します。天体が相対的に小さい場合 (小惑星のように) にはその軌道がわずかに変化する可能性があります。遠日点において、小惑星は隣接する物体と比較してかなりゆっくりと動いているため後ろから衝突されやすく、近日点が近づくとその逆になります。このことによって i β2 (3q-2– q2) の比例項が (4) の右辺に追加され ([3] を参照) 、結果として β‘ の方程式を修正することがわかります。すなわち
となります (C は小さな値の定数) 。これを検証するために、結果の方程式の章のプログラムで C I β2 {3, 0, 1} (C i β2(3 q-2 – q2) に対するコード) を RHS に追加し、β のべき乗の追加を考慮にいれて β‘ を再計算します。
(16) の新たな項は、(12) に対応する解を以下のように修正します。
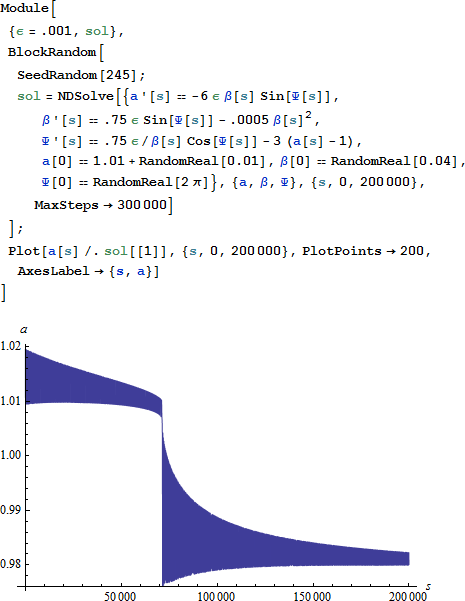
a、β、Ψ の初期値はランダムに生成されるので、(SeedRandom[245] を削除した後に) 間隙内から (あるいは下で) 始まることがあります。それにもかかわらず、プログラムを何回か実行することで、どのような初期条件でも a が間隙内 (おおよそ 0.99 < a < 1.01) にないことが実証されます。
今までに考察した 2つ (木星の重力と Kepler Shear) 以上に、小惑星には明らかに多くの他の摂動の作用があります。それらを個別に考えるより、(12) の最初の方程式の右辺に追加された新しい単一項 (このような項は、もっとも効果的に元の解の本質に明白な影響を与えるので) に組み合わせて考えてみます。新しい項は、実際にはゆっくりとした時間依存を持つかもしれませんが、問題を単純化するため、小さな値の定数とします。新たな方程式は次に、
を読み込みます。
κ > 0 の場合、古い解ではあまり影響されず、間隙の突然の交差がより速くなるだけです。状況が劇的に変化するのは κ < 0 の場合です。この場合 (C • κ ≪ ϵ2 かつ κ ≪ C の場合) 、ほとんどの解が導かれる間隙の下に、固定点があります (初期値が a > 1.01 以外の場合、つまり解がその引力の軌道の外にあり、間隙からゆっくり漂って離れていく場合以外) 。あらゆる可能性を探るために、(再度 SeedRandom[3] を削除した後に) 以下のプログラムを数回実行してこれを検証します。
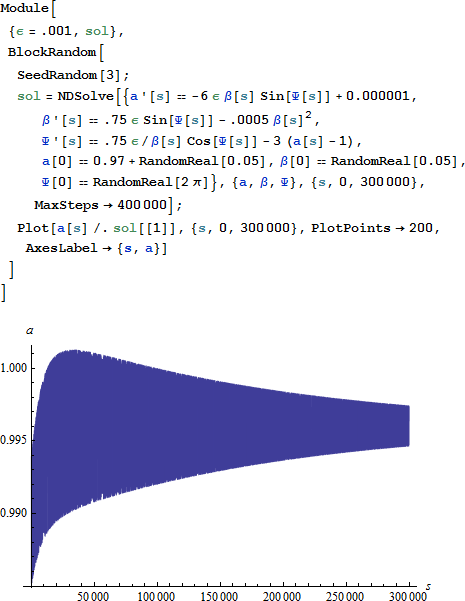
既に述べた通り、κ の値は、実際には、時間に従ってゆっくりと変化します。しかし、すでに見てきたように、その値や符合にかかわらず常に間隙は一掃されます。
同様の方法で、木星の離心率 (γ ≃ 0.05) を説明する場合、(12) の右辺には ϕ が現れ、三つの方程式を次の四つに展開する必要があることを意味しています。
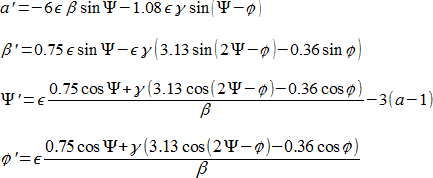
この時点ではまだ、Kepler Shear もしくは他のどんな付加的な摂動も含まれていません。
2:1 共鳴に近い、オリジナルの、まさに原則どおりの解がどのように変化するか見てみましょう。

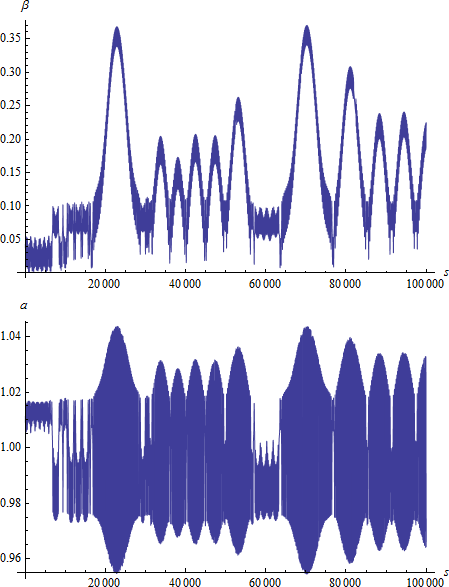
このような状況においては、解が完全なカオスになる (初期条件よって大きな差がでる) ことがあり、この場合、β はかなり大きな値になる可能性があります。さらに、a に興味深い事象は特に何も起こらず、この値は常に共鳴の範囲内にとどまります。よく間違って述べられますが、カオスは間隙を一掃する主な原因ではないことは明らかです。
2つの軌道面の間に 軌道傾斜面 がある場合は同じ結論に達します。この場合、6つの一連の微分方程式が必要で (ひとつは軌道傾斜面、その他は残ったオイラー角に対するもの) 、カオス解を得る可能性はわずかに高くなります。しかし、(元の解に決定的な摂動を追加しなければ) 間隙の一掃はみられません。
n : (n – 1) 形式の共鳴において (ここで n は小さな整数です) 、結果として生じる方程式とその結論は、2:1 の場合とほとんど完全に一致します (係数のみ異なります) 。よって例えば、3:2 共鳴に近い動きに対しては、
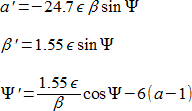
という式が得られます。
n : (n – 2) の共鳴においては、次数の高い β が各方程式の右辺において最高次になるため、状況は僅かに複雑になります。3:1 共鳴の重要なケース ([4] でも調査済) の結果を引用します。
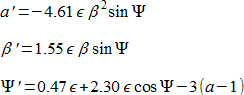
n : (n – 3) と n : (n – 4) の共鳴においても、同様の (Ψ‘ 以外の各方程式の右辺における β の次数の増加の) 傾向があります。よって、例えば、5:2 共鳴に対しては、
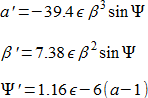
を得ます。そして 7:3 共鳴については
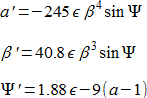
を得ます。
今度は (すなわち n : (n – 1) 以外の状況で) 、間隙を作り出す精密なメカニズムは 2:1 共鳴の状況とわずかに異なり、κ > 0 の場合、間隙の下に固定点は 1つもありません。その代わりに、κ < 0 の場合 (方向の逆転を除く) と同様に、a が間隙を素早く通過し、その値は一定に保たれます。ここで、7:3 の共鳴を使って実際にやってみましょう。
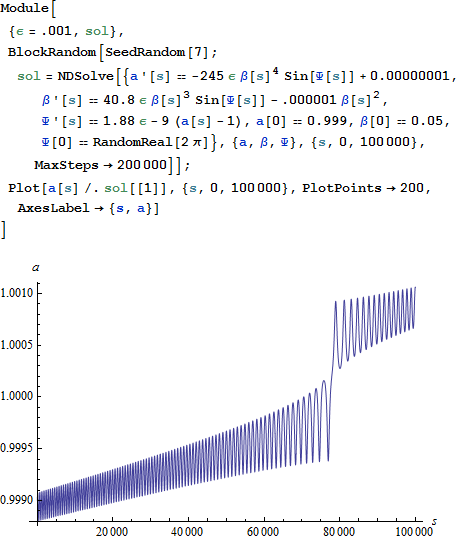

n : (n – k) 共鳴の一般的なケースでは、 k が増加するほど間隙が狭くなります。
J. Vrbik, "Mathematical Exploration of Kirkwood Gaps," The Mathematica Journal, 2012. doi:10.3888/tmj.14-1.