ハミルトン・ツアーの拡張を幾つか紹介。
1857年にウィリアム・ローワン・ハミルトンは Icosian Game を創りました [1]。12 面体のグラフに基づく世界で、旅人は同じ都市を訪れることなく、20 の都市を訪問しなければならないというものです。ツアー (旅人の経路) がグラフの全ての頂点でループを作るとき、それは Hamiltonian tour (もしくは cycle) と呼ばれます。ツアーの最初と最後の頂点がつながれないとき、それは Hamiltonian path (もしくは trail) と呼ばれます。一つ目の図は Hamiltonian tour、二つ目は Hamiltonian path を示しています。

Hamiltonian cycle は 1880年に P. G. Tait が、「あらゆる3次多面体には、すべての頂点を通過する Hamiltonian cycle が存在する」という予想を立てたもので人気を博しました。「3次」とは全ての頂点において 3本の辺が交わることを意味しています。3次の必要条件が無いと、Hamiltonian でない小さな多面体が存在してしまいます。最も単純な反例は菱形十二面体(Rhombic Dodecahedron)です。いずれの辺も、6個ある4次の頂点の1つと、8個ある3次の頂点の 1つとをつないでいます。長さ 14 のツアーにおいて、6個の4次の頂点はもう1つ3次の頂点と 1つおきに並べる必要があります。6個の4次の頂点では 8個の3次の頂点の間にある 7個のスロットを満たすことができないので、これは解くことができません。

どんな3次でないグラフでも、例外となる頂点の上に小さな丸○を置くことで、3次を作ることができます。

「多面体」という言葉はグラフが3連結でなければならないことを意味しています。地図を分断するために線を引くときは、その線は少なくとも3つの境界を通らなければなりません。スペインを通る線がポルトガルを分断するので、中央ヨーロッパは3連結ではありません。フランスやバチカン、様々な島があるので、ヨーロッパの形は非多面体になります。

Tait’s method は以下の方法によって、3次多面体グラフ上の Hamiltonian Cycle を4色で塗り分けます。

66年間、Tait の予想は破られませんでした。1946年に W.G.Tutte が現在 Tutte のグラフとして知られる最初の反例を見つけました。それ以降、いくつかのさらに小さな3次の Hamiltonian でない3次の多面体グラフが発見されました。最も小さいものは 1965年に見つかった Barnette-Bosak-Lederberg グラフです。それより7年早く Lederberg はノーベル生理学・医学賞を得ました。

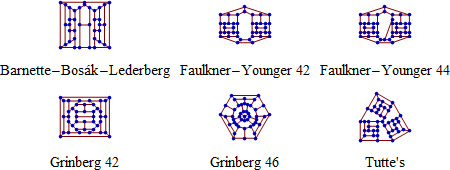
残念がら、ハミルトンの Icosian game には欠点があります。Hamiltonian path で繋がれない2つの頂点を選ぶことができます。改善するには Hamilton-connected graph を使います。Hamilton-connected graph はどの2つの頂点も Hamiltonian path によって繋がれるというグラフです [2]。 これらのグラフのさまざまな例は GraphData["HamiltonConnected"] で得られます。
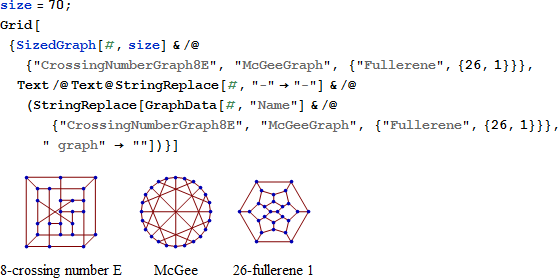
もっと簡単に解ける 26-fullerene グラフは次で与えられます [3]。頂点は正方形に置き換えられ、辺は隣接する正方形の間の辺か、四角形をつなぐ緑の線に置き換えられます。図の端の辺は、反対側の端の辺とつながっています。パズルを試すためには、A と Z を任意の2つの正方形に書いてください。それから A から Z の文字を使って、A と Z を繋ぐ Hamiltonian Path を探してください。どこに A と Z を配置したとしても、パズルを解くことができます。例えば、あなたがブロック 2 に A、ブロック 6 に Z を配置して始めると、2つの解答のうちの1つは、(A) → 2 → 3 → 4 → 8 → 7 → 15 → 16 → 9 → 10 → 5 → 1 → 14 → 13 → 26 → 25 → 24 → 21 → 20 → 19 → 23 → 22 → 17 → 18 → 11 → 12 → 6 → (Z) です。
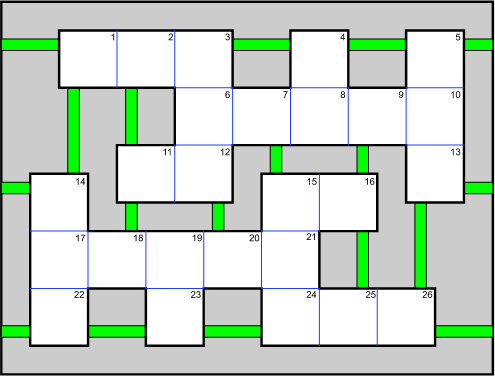
頂点 2 と 6 を繋ぐ見えない頂点を追加するという方法を使うことで、このパスを Mathematica で見つけて、描画することができます。

もっと難しいパズルとしては Coxeter グラフから辺を除いたものがあります。この Hamiltonian パズルの解きやすいバージョンはこちらです。
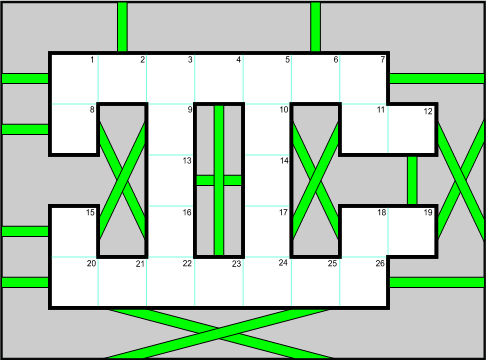
Ed Pegg Jr, "The Icosian Game, Revisited," The Mathematica Journal, 2010. doi:10.3888/tmj.11.3-1.