Focus on Special Features

Needle/Tunneling Optimization

When needle optimization finds an “optimal” design, that design may still not have the desired performance. Needle optimization has merely found a local minimum of the merit function.

The purpose of the tunneling method is to find another — better — local minimum. It does this by growing a layer — which has the effect of tunneling to another valley of the merit function. See the diagram below for a 2-layer example.

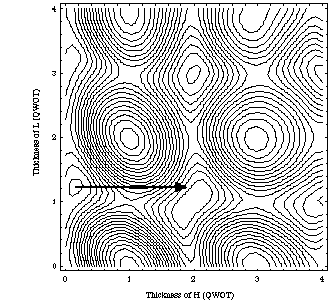
The arrow indicates how this method tunneled from one valley to another.

A benefit of the needle/tunneling method is that the initial design can be very simple — perhaps only 1 QWOT thick. The method will grow the design to meet the desired performance.

Another benefit is that a sequence of designs is created, giving the designer a choice of designs to manufacture.

Finally, this method excels at finding the thinnest design that meets a given performance specification; it just grows the design until the requirement is attained. For an example of this, see Growing an Antireflection Coating.